Контрольная работа № 2. Программирование с использованием циклических алгоритмов

Задание 2.1. Циклы с известным числом повторений

Целью работы является освоение программирования алгоритмов с циклической структурой, когда какой-либо участок программы выполняется определенное количество раз.

Типичный пример циклического процесса – вычисление конечных сумм. При определении сумм многократно вычисляется выражение, стоящее под знаком суммы и складывается с предыдущей частичной суммой. Вычисления производятся до тех пор, пока не будут сложены выражения под знаком суммы для всех значений изменяющейся переменной.

Пример: составить программу, вычисляющую значение суммы

.

Прежде чем вычислять выражение под знаком суммы и очередную частичную сумму, необходимо определить начальное значение параметра цикла (в данном случае i, которое изменяется от 1 до 10 с шагом 1, то есть i будет принимать последовательно значения 1, 2, 3, 4,..., 9, 10), и начальную частичную сумму S. Так как вычисления еще не производились, то S = 0.

Затем вычисляется выражение под знаком суммы для i = 1, затем i = 2, 3,... до 10 и каждый раз складывается с предыдущей частичной суммой S _{i -1}. При этом получается новая частичная сумма S _i. После этого i увеличивается на единицу и проверяется, не стало ли i > 10. Если еще меньше или равно 10, то вычисляется новая частичная сумма, в противном случае вычисление суммы будет закончено, и это значение выводится на печать.

Воспользуемся стандартной схемой циклического процесса, представленной на рис. 11.

Блок 2 – блок подготовки к вычислению суммы, в котором задаются начальные значения параметра цикла и частичной суммы.

Блок 3 – блок проверки окончания цикла. Необходимо проверить, стало ли i больше 10. Если стало, то цикл закончен, следующим должен выполняться блок печати. Если нет, то вычисление частичной суммы продолжается дальше, то есть выполняются блоки 4 и 5.

В блоке 4 производится вычисление выражения, стоящего под знаком суммы и сложение с предыдущей частичной суммой S _i-1. В итоге получается новая частичная сумма S _i.

В блоке 5 происходит изменение параметра цикла (увеличение i на 1). Это блок подготовки к новому циклу.

Проверка может осуществляться условным оператором IF, но для организации циклов в языке Паскаль специально предусмотрены три оператора цикла. Если количество повторений заранее известно и параметр является целым числом, то целесообразно использовать оператор FOR, включающий в себя блоки 2, 3, 5. В этом случае в алгоритме можно применить блок «Модификация».

Алгоритм для примера с использованием оператора FOR приведен на рис. 12. Варианты заданий – в табл. 3.

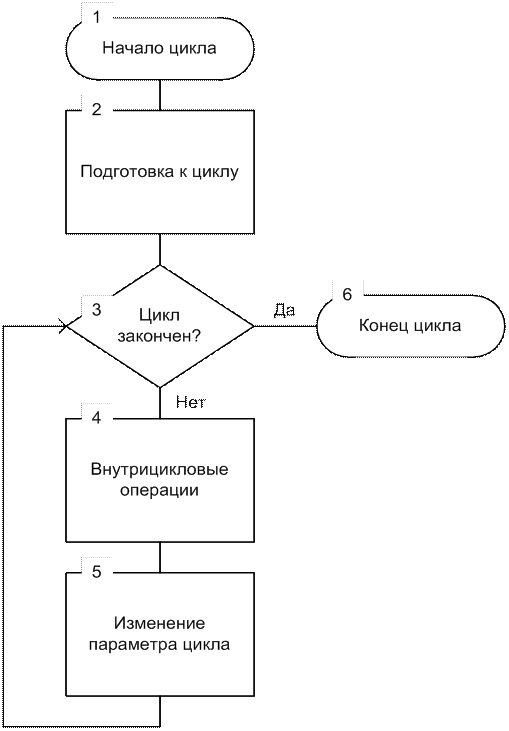
Рис. 11. Блок-схема алгоритма циклического процесса

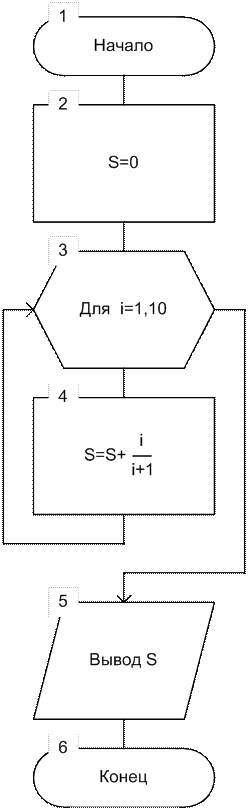
Рис. 12. Блок-схема алгоритма примера.

Таблица 3. Варианты заданий 2.1

№ вар.	Вычислить сумму	№ вар.	Вычислить сумму

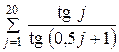
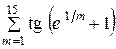
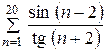
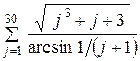
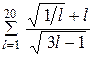
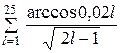
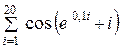
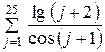
Продолжение табл. 3

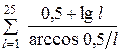
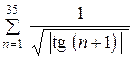
Задание 2.2. Двойные и кратные циклы

Целью работы является освоение программирования алгоритмов с вложенными циклами. Пример такой задачи – вычисление двойной суммы.

Пример: вычислить с точностью до 10^-4.

Здесь внешней суммой является сумма по i, а внутренней – сумма по j. Можно рассматривать вычисление этих сумм отдельно, учитывая что вычисление внутренней суммы является частью вычисления внешней суммы, то есть телом внешнего цикла.

Сами суммы в задании никак не обозначены, и им необходимо присвоить имена, которые могут быть относительно произвольные: SUM_IN ()внутренняя) и SUM_OUT (внешняя); SUMI и SUMO; S1 и S2 и другие. Так же обозначается и внутреннее слагаемое: SLAG, S и так далее.

Внешняя сумма по i вычисляется так же, как и в задании 1. Так как используется счетчик циклов, и количество слагаемых определено, то для ее вычисления справедлив алгоритм, представленный на рис. 12, кроме блока 4. Блок 4 – это не обычное суммирование, а внутренний цикл по вычислению суммы по j. Таким образом блок 4 замещается несколькими блоками, производящими вычисление внутренней суммы. Говорят, что цикл (суммирование) по j вложен в цикл по i.

Внутренняя сумма по j является примером суммы с бесконечным верхним пределом. Проверка окончания цикла осуществляется следующим образом. Так как выражение под знаком суммы постепенно убывает с ростом слагаемых в сумме, то наступает момент, когда очередное слагаемое станет меньше наперед заданного числа e (грубо говоря, точности вычисления сумм), и остальные слагаемые будут мало влиять на конечный результат. Поэтому, когда выражение под знаком суммы | f (j) | будет меньше e, то вычисления прекращаются и предполагается, что сумма найдена с заданной точностью. Если возможны отрицательные значения под знаком суммы, то обязательно надо использовать функцию вычисления модуля, так как число -10 меньше 10^-4 (0.0001), но заданная точность еще не достигнута.

Так как количество слагаемых заранее неизвестно, то циклом FOR пользоваться нельзя. Для этих целей предназначаются циклические операторы WHILE (соответствует блок-схеме, приведенной на рис. 11) и REPEAT. Необходимо помнить, что у них параметр цикла автоматически не изменяется и его надо менять принудительно, а при составлении блок-схемы алгоритма вычисления внутренней суммы (вместо блока 4, рис. 12.) блок «Модификация» не используется.

При вычислении суммы в некоторых вариантах должен вычисляться факториал по формуле:

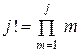
Где П – знак произведения (аналогично знаку суммы), то есть 5! = 1· 2· 3· 4· 5 = 120. Факториал можно вычислить отдельным циклом, третьим, а можно и прямо в цикле вычисления внутренней суммы. Для этого вводится дополнительная переменная, например f = j!, и затем в цикле умножается на текущее значение j.

Кроме значения суммы на экран при отладке полезно вывести значение счетчика циклов, то есть узнать, из скольких слагаемых состоит каждая сумма.

Примечание. В языке Турбо Паскаль под переменные типа INTEGER выделяется два байта, и допустимые для них значения находятся в диапазоне только от -32768 до 32767. Поэтому число 10!, реально равное 3628800, в этом случае будет представлено как 24320. Таким образом выражение под знаком суммы может никогда и не стать меньше заданной точности. Для работы с большими целыми числами (факториалом) во избежание переполнения рекомендуется использовать вещественный тип Real с диапазоном представления от 2.9·10^-39 до 1.7·10³⁸, или целый тип LongInt с диапазоном от -2.147.483.648 до 2.147.483.647.

При составлении программы точность обязательно должна задаваться в форме вещественного числа с плавающей точкой, а вывод суммы выполняться с фиксированной точкой и количеством знаков дробной части, соответствующим заданной точности.

Варианты заданий контрольной работы приведены в табл. 4.

Таблица 4. Варианты заданий 2.2

№ вар.	Вычислить	Точность вычислений e
		10^-3
		10^-4
		10^-3
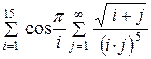
		10^-4
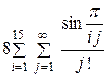
		10^-3
		10^-4
		10^-3
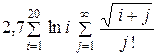
		10^-4
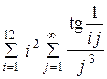
		10^-3
		10^-4

Продолжение табл. 4

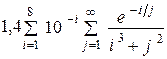
		10^-3
		10^-4
		10^-3
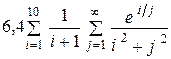
		10^-4
		10^-3
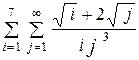
		10^-4
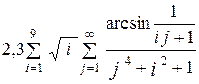
		10^-3
		10^-4
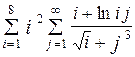
		10^-3
		10^-4

Окончание табл. 4

		10^-3
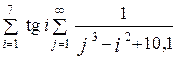
		10^-4
		10^-3
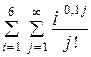
		10^-4
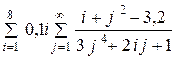
		10^-3
		10^-4
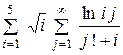
		10^-3
		10^-4
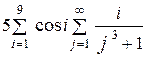
		10^-3
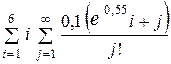
		10^-4

ПРИЛОЖЕНИЕ А

Таблица 5. Основные команды интегрированной инструментальной оболочки Турбо Паскаль 7.0

Команда меню	«Горячая клавиша»	Функция
-	F10	Активизация строки меню
-	<Alt+F10>	Вызов локального меню
-	<Alt+Литера>	Открытие озаглавленного выбранной литерой подчиненного меню из строки меню
New	-	Создание нового окна с именем NONAMEnn.PAS для ввода программы
File/ Open	F3	Открытие нового окна и загрузка в него выбранного файла
File/ Save	F2	Сохранение на диске файла из активного окна. Если было создано новое окно, выполнится команда Save as
File/ Save as	-	Сохранение на диске файла из активного окна с запросом на новое имя файла
File/ Cnange dir	-	Смена текущей директории
File/ Exit	<Alt+X>	Завершение сеанса работы с Турбо Паскалем с сохранением (после подтверждения) файлов, измененных редактором текста
Edit/ Undo	<Alt+ Backspace>	Отмена всех изменений в текущей строке
Edit/ Cut	<Shift+Del>	Перенос выделенного блока в буфер промежуточного хранения

Продолжение табл. 5

Edit/ Copy	<Ctrl+Ins>	Копирование блока в буфер промежуточного хранения
Edit/ Paste	<Shift+Ins>	Копирование блока из буфера промежуточного хранения в окно редактирования
Edit/ Clear	<Ctrl+Del>	Удаление выделенного блока
Run/ Run	<Ctrl+F9>	Компиляция и выполнение программы под управлением интегрированной инструментальной оболочки
Run/ Step over	F8	Трассировка программы пооператорно с выполнением подпрограмм без пооператорной детализации
Run/ Trace Into	F7	Трассировка программы пооператорно с пооператорным выполнением всех подпрограмм
Run/ Go to Cursor	F4	Выполнение программы, расположенной в активном окне, до позиции курсора
Run/ Program Reset	<Ctrl+F2>	Установка программного счетчика на начало программы и закрытие всех ранее открытых программой файлов
Compile/ Compile	<Alt+F9>	Компиляция программы из активного окна
Compile/ Make	F9	Компиляция и редактирование связей программы
Compile/ Destination Memory/Disk	-	Место компиляции программы: либо в оперативную память, либо на диск
Debug/ Call Stack	<Ctrl+F3>	Открытие окна протокола используемых процедур

Окончание табл. 5

Debug/ User Screen	<Alt+F5>	Переключение на пользовательский экран
Debug/ Evaluate/ Modify	<Ctrl+F4>	Просмотр и изменение значений переменных
Debug/ Add Watch	<Ctrl+F7>	Дополнение списка переменных, наблюдаемых в Watch-окне
Option/ Save TURBO.TP	-	Сохранение конфигурации ИИО в файле TURBO.TP
Window/ Size/ Move	<Ctrl+F5>	Изменение положения и размера окна
Window/ Zoom	F5	Изменение (увеличение/ уменьшение) размера активного окна
Window/ Next	F6	Переход к следующему окну
Window/ Previous	<Shift+F6>	Возврат к предыдущему окну
Window/ Close	<Alt+F3>	Закрытие активного окна
Window/ List	<Alt+0>	Вызов окна, в котором содержится список всех открытых окон
-	<Alt+Цифра>	Переход к окну с указанным номером
-	F1	Активизация окна контекстно-зависимой помощи
Help/ Previous topic	<Alt+F1>	Возврат к предыдущей справке
Help/ Topic search	<Ctrl+F1>	Активизация синтаксической справки, то есть справки об операторе, на который указывает маркер
Help/ Index	<Shift+F1>	Вызов содержания справочной подсистемы

ПРИЛОЖЕНИЕ Б

Таблица 6. Команды редактора текста. Управление курсором

Клавиши	Действие
Стрелка вверх	Курсор переводится на одну строку вверх
Стрелка вниз	Курсор переводится на одну строку вниз
Стрелка влево	Курсор переводится на одну позицию влево
Стрелка вправо	Курсор переводится на одну позицию вправо
<Ctrl+Стрелка влево>	Курсор переводится на одно слово влево
<Ctrl+Стрелка вправо>	Курсор переводится на одно слово вправо
Home	Курсор переводится на начало строки
End	Курсор переводится в конец строки
<Ctrl+Home>	Курсор переводится на первую строку экрана
<Ctrl+End>	Курсор переводится на последнюю строку экрана
PgUp	Продвижение по файлу на одну страницу назад
PgDn	Продвижение по файлу на одну страницу вперед
<Ctrl+PgUp>	Курсор переводится в начало файла
<Ctrl+PgDn>	Курсор переводится в конец файла
<Ctrl+W>	Экран сдвигается «вверх» по тексту (при этом курсор неподвижен)
<Ctrl+Z>	Экран сдвигается «вниз» по тексту (курсор неподвижен)
<Ctrl+Q>+B	Курсор переводится в начало блока

Продолжение табл. 6

<Ctrl+Q>+K	Курсор переводится в конец блока
<Ctrl+Q>+P	Курсор перемещается на исходную позицию после поиска
<Ctrl+P>	Ввод специального символа
Вставка и удаление
Del	Удаление символа, указываемого курсором
Ins	Переключение между режимами вставки и замены
BackSpace	Удаление символа слева от курсора
<Ctrl+T>	Удаление слова справа от курсора
<Ctrl+Q>+Y	Удаление части строки от курсора до конца строки
<Ctrl+Y>	Удаление строки, указываемой курсором
<Ctrl+Q>+L	Восстановление строки, удаленной комбинацией клавиш <Ctrl+Y>, в том месте текста, где она была расположена
<Ctrl+N>	Вставка строки
Операции с блоками
<Shift+стрелки>	Расширение маркируемого блока
<Ctrl+K>+B	Указание начала маркируемого блока
<Ctrl+K>+K	Указание конца маркируемого блока
<Ctrl+K>+T	Маркирование слова
<Ctrl+K>+H	Снятие/ восстановление маркировки
<Ctrl+K>+I	Сдвиг маркированного блока вправо

Продолжение табл. 6

<Ctrl+K>+U	Сдвиг маркированного блока влево
<Ctrl+K>+C	Копирование маркированного блока в то место, где установлен курсор
<Ctrl+K>+V	Перенос маркированного блока в то место, кде установлен курсор
<Ctrl+Ins>	Копирование маркированного блока в буфер промежуточного хранения (Edit/ Copy)
<Shift+Del>	Перенос маркированного блока в буфер промежуточного хранения (Edit/ Cut)
<Shift+Ins>	Копирование маркированного блока из буфера промежуточного хранения в то место, где установлен курсор (Edit/ Paste)
<Ctrl+K>+Y	Удаление маркированного блока
<Ctrl+K>+P	Печать маркированного блока (File/ Print)
<Ctrl+K>+R	Вставка текста из файла в позицию, указываемую курсором (Read)
<Ctrl+K>+W	Запись блока в файл (Write)
<Ctrl+K>+F	Переключатель режима заполнения, позволяющий оптимизировать заполнение интервалов между словами (пробелами/ табуляциями) (Options/ Env./ Editor/ Optimal Fill)

Окончание табл. 6

Поиск и замена
<Ctrl+Q>+F	Поиск указанной строки (Search/ Find). Для указания опций открывается специальное окно
<Ctrl+Q>+A	Поиск указанной строки и замена(Search/ Replace). Для указания опций открывается специальное окно
<Ctrl+Q>+[	Поиск разделителя ({, [, (, ",'), парного по отношению к указываемому курсором (удобно искать границы комментариев)
<Ctrl+Q>+]	Поиск разделителя (], },), ",'), парного по отношению к указываемому курсором
<Ctrl+K>+<n>	Установка отметки в тексте. n - цифра от 0 до 9
<Ctrl+Q>+<n>	Перевод курсора на отметку в тексте. n - цифра от 0 до 9
<Ctrl+Q>+W	Перевод курсора на позицию, где дано сообщение об ошибке
<Ctrl+L>	Продолжение поиска/ замены с установленными ранее опциями
<Ctrl+U>	Прерывание поиска/ замены

Список литературы

1. Зуев Е.А. Язык программирования Turbo Pascal 6.0, 7.0. – М.: Веста, Радио и связь, 1993.

2. Климова Л.М. PASCAL 7.0: Практическое программирование. Решение типовых задач.: Учебное пособие. – М.,: 2000.

3. Немюгин С.А. TURBO PASCAL – СПб, 2000.

4. Турбо Паскаль 7.0. Самоучитель. – СПб.: Питер; К.: Издательская группа BHV, 2002. – 416 с.: ил.

5. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: «Нолидж», 1999. – 616 с., ил.

6. Федоренко Ю. Алгоритмы и программы на Turbo Pascal. Учеб. Курс. – СПб.: Питер, 2001.

Дата добавления: 2014-11-16