
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Их перпендикулярности 1 страница
Если векторы 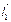 ,
, 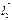 ,
,  образуют базис в пространстве, то любой вектор
образуют базис в пространстве, то любой вектор  единственным образом можно разложить по базису
единственным образом можно разложить по базису 
Если вектора 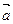 ,
, 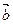 ,
, 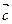 компланарны, то выполняется равенство
компланарны, то выполняется равенство 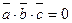
Если векторы 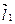 ,
,  ,
,  образуют базис в пространстве, то любой вектор
образуют базис в пространстве, то любой вектор  имеет следующее разложение
имеет следующее разложение 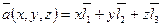
Если вектор нормали к плоскости 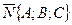 то общее уравнение плоскости имеет вид Ax+By+Cz+D=0
то общее уравнение плоскости имеет вид Ax+By+Cz+D=0
Если плоскость  проходит параллельно оси
проходит параллельно оси  , тогда только A=0, By+Cz+D=0
, тогда только A=0, By+Cz+D=0
Если плоскость  проходит параллельно оси
проходит параллельно оси 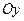 , тогда, только B=0, Ax+Cz+D=0
, тогда, только B=0, Ax+Cz+D=0
Если плоскость  проходит параллельно оси
проходит параллельно оси 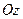 , тогда, только C=0, Ax+By+D=0
, тогда, только C=0, Ax+By+D=0
Если функция дифференцируема в точке 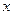 , то она непрерывна
, то она непрерывна
Если непрерывная функция 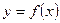 имеет производную
имеет производную 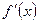 в точке
в точке 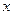 , то ее график имеет касательную, угловой коэффициент которой равен:
, то ее график имеет касательную, угловой коэффициент которой равен: 
Если функция 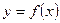 имеет на интервале
имеет на интервале 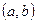 вторую производную и
вторую производную и  во всех точках
во всех точках 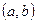 , то график функции вогнут
, то график функции вогнут
Если функция 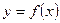 имеет на интервале
имеет на интервале 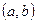 вторую производную и
вторую производную и  во всех точках
во всех точках 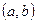 , то график функции выпукл
, то график функции выпукл
Если 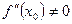 , то критическая точка
, то критическая точка 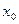 является точкой экстремума функции
является точкой экстремума функции 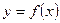 . При этом если
. При этом если  , то
, то 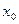 минимум
минимум
Если функция 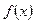 четная, то
четная, то 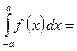 2F(a)
2F(a)
Если функция 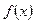 нечетная, то
нечетная, то 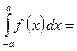 0
0 
Если функции  ,
, 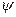 в параметрических уравнениях кривой
в параметрических уравнениях кривой  непрерывны на
непрерывны на  , то
, то 

Если кривая  задана уравнением
задана уравнением 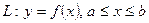 , тогда
, тогда 

Если кривая  задана полярным уравнением
задана полярным уравнением  ,
, 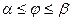 , то
, то 

Если функция 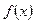 интегрируема на наибольшем из отрезков
интегрируема на наибольшем из отрезков  ,
,  и
и 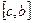 , то
, то 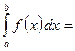

Если функции  ,
,  интегрируемы на
интегрируемы на  и
и 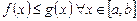 , то
, то 
Если функция 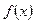 непрерывна на
непрерывна на  и функция
и функция 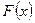 некоторая ее первообразная, то
некоторая ее первообразная, то
 F(b) – F(a)
F(b) – F(a)
Если  , то
, то  aF(x)+C
aF(x)+C
Если  , то
, то 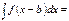 F(x)+bx+C
F(x)+bx+C
Если 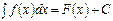 , то
, то  aF(x)+bx+C
aF(x)+bx+C
Если функция 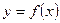 имеет в точке
имеет в точке 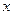 конечную производную
конечную производную 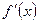 , то ее приращение может быть представлено в виде
, то ее приращение может быть представлено в виде 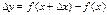
Если 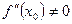 , то критическая точка
, то критическая точка 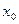 является точкой экстремума функции
является точкой экстремума функции 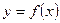 . При этом если
. При этом если  , то
, то 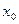 максимум
максимум
Если  , то
, то 
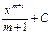
Если  ,
,  , то
, то 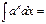



Если 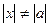 , то
, то 

Если 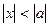 , то
, то 
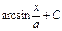
Если  - дифференцируемые функции, то
- дифференцируемые функции, то 
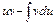
Если знак функции 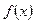 меняется на
меняется на  конечное число раз, то площадь
конечное число раз, то площадь 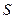 плоской фигуры, ограниченной линиями
плоской фигуры, ограниченной линиями  ,
, 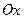 ,
,  ,
, 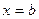 , равна
, равна 
Используя второй достаточный признак экстремума, найти экстремум функции 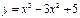 x1=0 - максимум, x2=2 - минимум
x1=0 - максимум, x2=2 - минимум
Исследовать на экстремум функцию  x1=-2 - максимум, x2=3 - минимум $$$ 79
x1=-2 - максимум, x2=3 - минимум $$$ 79
Квадратная матрица называется единичной, если у нее по главной диагонали стоят единицы, а все остальные элементы равны 0
Каноническое уравнение гиперболы 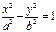
Каноническое уравнение эллипса 
Каноническое уравнение гиперболы 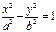
Каноническое уравнение параболы y2=2px
Каноническое уравнение прямой  , то прямая параллельна вектору
, то прямая параллельна вектору 
Какие из следующих функций непрерывны в точке 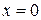 1)
1)  2)
2)  3)
3) 
3)
Какие из следующих функций являются бесконечно малыми одного порядка при 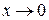
1)  2)
2)  3)
3)  4)
4)  1) и 2)
1) и 2)
Какие из следующих функций непрерывны в точке 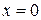 1)
1)  2)
2) 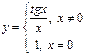 3)
3)  1) и 2)
1) и 2)
Какие из следующих функций непрерывны в точке 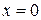 1)
1) 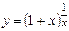 2)
2)  3)
3)  1)
1)
Какие из следующих функций являются бесконечно малыми одного порядка при 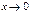 1)
1) 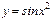 2)
2) 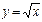 3)
3) 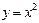 4)
4)  1) и 3)
1) и 3)
Какие из следующих функций являются бесконечно малыми одного порядка при  1)
1)  2)
2)  3)
3)  4)
4) 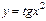 1) и 2)
1) и 2)
Какие из следующих функций являются бесконечно малыми одного порядка при 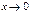 1)
1)  2)
2)  3)
3) 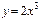 4)
4) 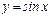 1) и 3)
1) и 3)
Модуль вектора  равен
равен 
Матрицы  размерности
размерности  и
и 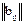 размерности
размерности  называются равными, если m=p, n=q, aij=bij
называются равными, если m=p, n=q, aij=bij
Минором 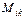 элемента
элемента 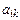 определителя
определителя  называется: определитель на порядок ниже, полученный из оставшихся элементов после вычеркивания i-той строки и j-того столбца, на пересечении которых находится элемент
называется: определитель на порядок ниже, полученный из оставшихся элементов после вычеркивания i-той строки и j-того столбца, на пересечении которых находится элемент
Найти 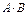 , если
, если 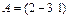 и
и  ; -5
; -5
Найти 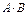 , если
, если 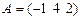 и
и 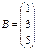 ; 21
; 21
Найти 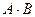 , если
, если 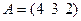 и
и 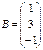 ; 11
; 11
Найти 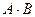 , если
, если  и
и 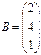 ; 17
; 17
Найти 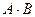 , если
, если  и
и  ; 4
; 4
Найти 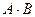 , если
, если  и
и 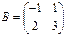 ;
; 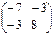
Найти значение 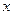 из системы
из системы 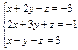 ; x=2
; x=2
Найти значение 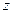 из системы
из системы  ; z=1
; z=1
Найти алгебраическое дополнение 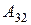 определителя
определителя 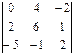 ; -4
; -4
Найти алгебраическое дополнение  определителя
определителя  ; -8
; -8
Найти 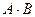 , если
, если 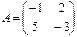 и
и  ;
; 
Найти 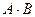 , если
, если 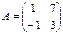 и
и  ;
; 
Найти 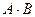 , если
, если  и
и  ;
; 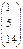
Найти 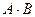 , если
, если 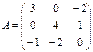 и
и  ;
; 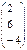
Найти уравнение  ;
; 
Найти алгебраическое дополнение 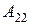 определителя
определителя 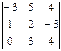 ; -12
; -12
Найти алгебраическое дополнение  определителя
определителя  ; 18
; 18
Найти алгебраическое дополнение 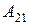 определителя
определителя  ; -6
; -6
Найти матрицу  , если
, если 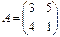 и
и 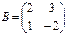 ;
; 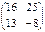
Найти матрицу 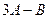 , если
, если  и
и 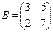 ;
; 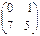
Найти 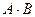 , если
, если 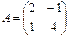 и
и 
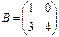 ;
; 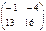
Найти значения 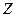 из системы
из системы  ; z=3
; z=3
Найти значение 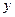 из системы
из системы  ; y=-1
; y=-1
Найти скалярное произведение векторов 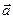 ,
, 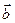 , если
, если 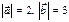
 ;
; 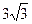
Найти 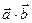 , если
, если  ,
, 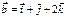 ; 3
; 3
Найти длину вектора 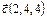 ; 6
; 6
Найти направляющие косинусы вектора 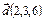 ;
; 
Найти координаты вектора  , если
, если  ,
, 

Найти длину вектора  , если
, если 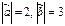 ,
, 

Найти длину вектора 
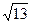
Найти скалярное произведение векторов  и
и 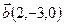
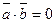
Найти проекцию вектора 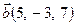 на вектор
на вектор 
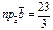
Найти  , если
, если 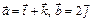
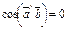
Найти  , если для векторов выполняется
, если для векторов выполняется 
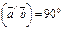
Найти проекцию вектора 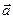 на вектор
на вектор 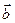 , если
, если 

Найти координаты вектора  , если заданы точки
, если заданы точки  и
и 

Найти вектор  , если
, если  и
и 
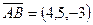
Найти модуль вектора 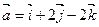

Найти длину вектора 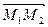 , если
, если 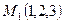 и
и 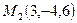
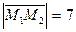
Найти скалярное произведение векторов  и
и 
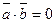
Найти  , если
, если 
 =13
=13
Найти единичный вектор того же направления, что и вектор 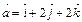

Найти работу силы  при перемещении
при перемещении  , если
, если 
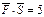
|
|
Дата добавления: 2014-11-16; Просмотров: 289; Нарушение авторских прав?; Мы поможем в написании вашей работы!