
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операторы
|
|
|
|
Оператор – это основной элемент языка программирования, представляющий собой законченную фразу и определяющий некоторый логически завершенный этап обработки данных.
Операторы условно можно подразделить на две категории: исполняемые – с их помощью реализуется алгоритм решаемой задачи, и описательные, необходимые для определения типов пользователя и объявления объектов программы, например, переменных.
Среди исполняемых операторов можно выделить:
· простые операторы (оператор-выражение, операторы передачи управления);
· составные операторы (составной оператор, блок)
· структурированные операторы (условный, выбора, цикла).
Рассмотрим простые операторы
Оператор «выражение»
Любое выражение, завершающееся точкой с запятой, рассматривается как оператор, выполнение которого заключается в вычислении выражения. Частным случаем выражения является пустой оператор (;). Он используется, когда по синтаксису оператор требуется, а по смыслу нет.
Примеры:
x ++; // выражение – оператор; выполняется операция инкремента
c = a * 1.5; // выражение с операцией присваивания
a *= b + c; // выполняется умножение с присваиванием: a = a * (b + c)
fun(i, k); // выполняется вызов функции
Оператора присваивания в языке С++ нет, его заменяет выражение, в составе которого есть операция присваивания.
Общий вид:
идентификатор = выражение;
Пример: x = y + 4; // выражение с операцией присваивания
Выполняется в два этапа:
а) вычисляется значение выражения, стоящего в правой части от знака присваивания;
б) вычисленное значение присваивается переменной, стоящей в левой части от знака присваивания, при этом предыдущее значение этой переменной теряется.
Рекомендуется строго относиться к типам данных, не смешивать типы в выражениях, следить, чтобы тип левого операнда присваивания соответствовал типу выражения правой части.
При выполнении присваивания, если типы левой и правой части не совпадают, происходит неявное преобразование. С++ всегда пытается это сделать, и упрощенно можно считать, что преобразование происходит без потери данных от меньшего типа к большему, например от int к float или от char к int, и с потерей данных от большего типа к меньшему, например, от float к int. Это легко понять, если вспомнить, что тип данного, это объем занятой им памяти.
Явное преобразование типов выполняется при присваивании вида:
имя = (тип) выражение;
Например:
int a = 5, b = 2;
float c;
с = a / b;
Хочется думать, что значение с будет равно 2.5, ведь оно вещественное, но порядок операций таков, что деление старше присваивания, и оно выполняется с операндами целого типа, и его результат равен 2, то есть приведение типа будет выполнено только при присваивании.
Для явного преобразования типов используется известный прием:
c = (float) a / (float) b; // c = 2.5
Операция присваивания правоассоциативна, т.е. вычисления выполняются справа налево, поэтому допускается запись цепочек присваиваний, например:
x = y =z = 1; // Каждая переменная будет равна 1.
В сложных операциях присваивания (+=, *=, /= и т п.) при вычислении выражения, стоящего в правой части, используется и L-значение из левой части. Например, при сложении с присваиванием ко второму операнду прибавляется первый, и результат записывается в первый операнд, то есть выражение a += b является более компактной записью выражения a = a + b.
Еще один вид операторов, который можно отнести к операторам-выражениям, это оператор обращения к функции (вызов функции). Его операндам являются параметры функции.
Формат оператора:
имя функции ([список фактических параметров] – может отсутствовать);
Например:
scanf ("%d%f", &my_int, & my_float); // ввод данных
printf ("Целое = %d, Вещественное = %f\n", my_int, my_float) // вывод
Пробелы в строке текста являются значащими, то есть, если ввести целое 5 и дробное 9.9, то строка вывода будет иметь вид:
Целое = 5, Вещественное = 9.900000
Операторы передачи управления рассмотрим позже (п. 3.6, п. 4.1)
2.7. Организация ввода/вывода данных
Ввести данное – означает присвоить произвольное значение переменной во время выполнения программы. Вывести данное – означает напечатать на экране значение переменной при выполнении программы.
В С++ нет встроенных средств ввода/вывода – он осуществляется с помощью функций, типов и объектов, содержащихся в стандартных библиотеках.
Лабораторная работа № 2
Программирование алгоритмов линейной структуры
ЦЕЛЬ РАБОТЫ: закрепление знаний о типах данных, преобразованиях типов, приобретение навыков составления и отладки программ линейной структуры на языке программирования C++
Выполнение работы: в соответствии с вариантом составить и реализовать программы.
Задание I
Написать программу для расчета по двум формулам. Предварительно подготовить тестовые примеры для второй формулы с помощью калькулятора (результаты вычисления по обеим формулам должны совпадать). Список стандартных математических функций C++ приведен в приложении 2. Отсутствующие в языке функции выразить через имеющиеся.
1. 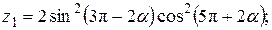 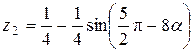 . .
|
2. 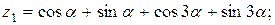 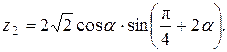
|
3. 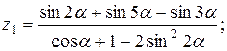 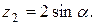
|
4. 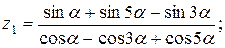 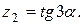
|
5. 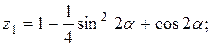 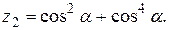
|
6. 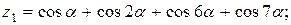 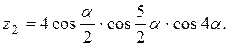
|
7. 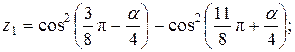 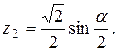
|
8. 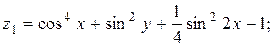 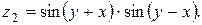
|
9. 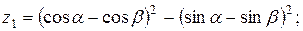 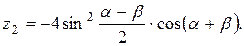
|
10. 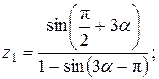 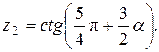
|
11. 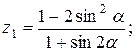 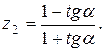
|
12. 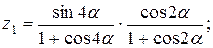 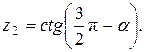
|
13. 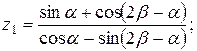 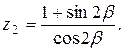
|
14. 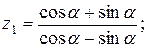 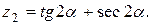 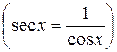 . .
|
15. 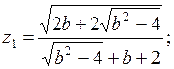 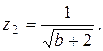
|
16. 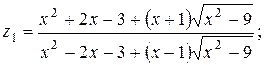 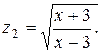
|
17. 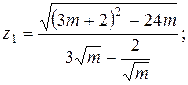 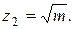 (m > 0) (m > 0)
|
18. 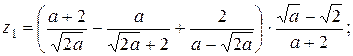 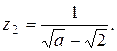 (a > 0) (a > 0)
|
19. 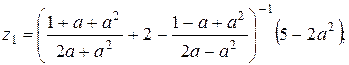 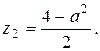
|
20. 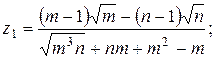 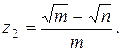
|
21. 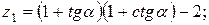 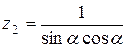 . .
|
22. 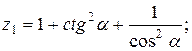 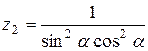 . .
|
23. 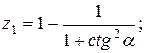 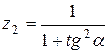 . .
|
24.  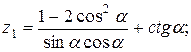 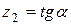 . .
|
25. 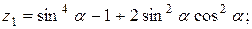 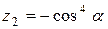 . .
|
Задание II
1. Составить программу вычисления объема конуса по заданному диаметру и образующей.
2. Дана сторона равностороннего треугольника. Составить программу нахождения площади этого треугольника и радиуса описанной окружности.
3. Известны радиусы двух концентрических окружностей. Составить программу нахождения площади кольца, образованного этими окружностями.
4. Составить программу нахождения суммы n членов арифметической прогрессии, для которой известен первый член, разность и число n.
5. Вычислить объем призмы, боковые грани которой - квадраты, а основанием служит равносторонний треугольник, вписанный в круг радиуса r.
6. Вычислить площадь прямоугольника, вписанного в окружность радиуса r, если отношение его сторон равно R.
7. Даны две стороны треугольника и угол между ними. Определить третью сторону и площадь.
8. Вычислить процент материала, ушедшего в отходы, если из куба с ребром а был выточен шар радиуса r (r < а).
9. Вычислить площадь кольца, ширина которого равна а, а отношение радиусов окружностей равно b.
10. Вычислить периметр и площадь прямоугольного треугольника, описанного около круга радиуса r, если гипотенуза треугольника равна с.
11. Вычислить диаметр трубы, пропускная способность которой позволяет заменить ею две трубы с диаметрами d 1 и d 2.
12. Вычислить высоты треугольника со сторонами a, b и с.
13. Вычислить площадь правильного n -угольника, описанного около круга радиусом r.
14. Высота конуса равна h, а радиус основания r. Вычислить объем шара, вписанного в конус.
15. Вычислить массу свинцовой трубы, длина которой равна b м (плотность свинца равна 11,4 г/см3), толщина стенок а мм, а внутренний диаметр трубы равен d мм.
16. Дан равносторонний треугольник. Вычислить сторону, высоту и площадь этого треугольника, если радиус вписанной окружности равен r.
17. Стальной вал, имеющий b мм длины и d мм в диаметре, обтачивается на токарном станке, при этом диаметр уменьшается при обточке на S мм. Вычислить, на сколько уменьшается масса тела (плотность стали 7,4 г/см3).
18. Вычислить объем призмы, боковые грани которой – квадраты. Основанием призмы служит равносторонний треугольник, заданный длиной стороны.
19. В конус с радиусом основания r и высотой h вписан цилиндр, радиус основания которого равен а. Вычислить объем цилиндра.
20. Даны две стороны треугольника d и с и угол между ними a. Найти радиусы окружностей: вписанной в треугольник и описанной около него.
21. Дана длина ребра куба. Найти объем куба и площадь его боковой поверхности.
22. Треугольник задан тремя сторонами. Вычислить его высоты.
23. Определить периметр правильного n -угольника, описанного около окружности радиуса R.
24. Смешано V 1 литров воды температуры Т 1 и V 2 литрами воды температуры Т 2. Найти объем и температуру образовавшейся смеси.
25. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
26. Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности.
27. Найти площадь кольца, внутренний радиус которого равен R 1, а внешний - R 2 (R 2 > R l).
28. Определить время, через которое встретятся два тела, равноускоренно движущиеся навстречу друг к другу, если известны их начальные скорости, ускорение, начальное расстояние между ними.
29. Вычислить расстояние между двумя точками с координатами (x 1, y 1) и (x 2, y 2).
30. Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
Задание III
1. Радоновые ванны, применяемые для лечения, содержат 1.8·106 атомов радона в воде объемом 1.0 дм3. На сколько молекул воды приходится один атом радона в лечебной ванне?
2. Сколько атомов ртути содержится в воздухе объемом 1.0 м3 в помещении, зараженном ртутью, при температуре 20°С, если давление насыщенного пара ртути при этой температуре 133 мПа?
3. Какова длина ребра куба, содержащего 1.0·106 молекул идеального газа при нормальных условиях?
4. При какой температуре молекулы гелия имеют такую же среднюю скорость, как молекулы кислорода при 23°С?
5. Найдите среднюю кинетическую энергию поступательного движения молекул водорода, если при давлении 0.5 атм. их концентрация равна 1.5·109 м-3.
6. Газ нагревается в открытом сосуде при нормальном атмосферном давлении от 27°С до 327°С. Какое приращение получает при этом число молекул в единице объема газа?
7. В сосуде объемом 1 дм3 содержится некоторый газ при температуре 17°С. Найти приращение давления газа, если вследствие утечки газа из него выйдет 1021 молекул.
8. В сосуде объемом 3.0 дм3 находится гелий массой 4.0 мг, азот массой 70 мг и 5.0·1021 молекул водорода. Каково давление смеси, если температура ее 27°С?
9. Определить среднюю кинетическую энергию вращательного движения молекул водорода, содержащихся в 1.0 моль при 18°С.
10. При какой температуре молекулы кислорода имеют такую же среднюю скорость, как молекулы водорода при 25°С?
11. Сколько молекул содержится при нормальных условиях в 1м3 воздуха?
12. В сосуде объемом 2.0 дм3 находится газ под давлением 0.50 МПа. Чему равна средняя кинетическая энергия поступательного движения молекул газа?
13. Кислород массой 12 г находится при температуре 700°С, при этом 40% молекул диссоциировано на атомы. Чему равна средняя кинетическая энергия теплового движения частиц? Колебательные степени свободы молекул кислорода не возбуждаются.
14. Объём помещения 50 м3. температура воздуха зимой 0°С, а летом – 40°С. Какова разница в массе воздуха, заполняющего помещение зимой и летом? Принять μ = 29 кг/моль.
15. Плотность воздуха при нормальных условиях 1.3 г/л. Какова плотность воздуха при температуре 100°С и давлении 4.0·105 Н/м2?
16. Температура воздуха в баллоне объёмом 10 м3 при давлении 700 мм рт. ст. была 15°С. После нагрева воздуха до 20°С часть воздуха была вытеснена. Найдите массу вытесненного воздуха.
17. Сколько частиц (атомов и молекул) находится в азоте массой 1.0 г, если степень диссоциации азота 7.0%.
18. Какое давление на стенки сосуда производит кислород, если средняя квадратичная скорость его молекул 400 м/с и концентрация молекул 2.7·1019 м-3?
19. Найдите среднюю кинетическую энергию поступательного движения молекул гелия, если при давлении 0.5 атм. их концентрация равна 1.5·109 м3.
20. Определите температуру газа, если средняя кинетическая энергия поступательного движения его молекул равна 1.6·10-19 Дж.
21. Каково давление газа, если в каждом кубическом сантиметре его содержится 1.0·106 молекул, а температура газа 87°С?
22. Газ нагревается в открытом сосуде при нормальном атмосферном давлении от 22°С до 320°С. Какое приращение получает при этом число молекул в единице объема газа?
23. В сосуде объемом 15.0 дм3 находится газ под давлением 0.50 МПа. Чему равна средняя кинетическая энергия поступательного движения молекул газа?
24. При какой температуре молекулы гелия имеют такую же среднюю скорость, как молекулы водорода при 27°С?
25. Газ занимает объём 2 л при давлении 5·105 Н/м2. Определите суммарную энергию поступательного движения молекул газа.
Задания для самостоятельной работы
1. Даны два действительных числа. Найти среднее арифметическое и среднее геометрическое этих чисел.
2. Даны четыре целых числа. Найти среднее арифметическое этих чисел и среднее геометрическое этих чисел.
3. Треугольник задан длинами своих сторон. Используя формулу Герона, найти площадь этого треугольника.
4. Идет k -я секунда суток. Определить сколько полных часов H, полных минут М прошло к этому моменту.
5. Даны два момента времени одних суток: H 1, H 2 - часы, M 1, M 2 - минуты. Определить интервал между этими моментами в часах H и минутах M.
6. По трем координатам вершин некоторого треугольника найти его высоту.
7. Найти объем и площадь боковой поверхности конуса радиусом r, высотой h и образующей l.
8. Вычислить боковую поверхность пирамиды (пирамида правильная, усеченная), если известны р и p 1 - полупериметры нижнего и верхнего оснований и k - апофема.
9. Найти объем и полную поверхность полого шара, если известны r 1 и r 2 - радиусы внешней и внутренней шаровых поверхностей.
10. Вычислить площадь поверхности и объем усеченного конуса высотой h, радиусами r 1 и r 2, образующей l.
11. В шар радиуса r вписан конус с углом а при вершине в осевом сечении конуса. Определить объем и полную поверхность конуса.
12. Вычислить объем цилиндра, вписанного в правильную шестиугольную призму, у которой каждое ребро равно а.
13. Найти площадь равнобокой трапеции с основаниями А и В и углом a при большем основании A.
14. Треугольник задан величинами своих углов и радиусом описанной окружности. Найти, стороны треугольника.
15. Найти объем правильной треугольной пирамиды, если стороны ее основания равны а и плоский угол при ее вершине равен a.
16. Вычислить радиус шара, вписанного в правильную четырехугольную пирамиду, если стороны основания пирамиды равны а и двухгранный угол при основании равен a.
17. Вычислить площадь круга и равнобедренной трапеции, описанной около него, если периметр трапеции равен р, а угол при нижнем основании равен а.
18. Вычислить объем призмы, боковые грани которой – квадраты. Основанием призмы служит равносторонний треугольник, по который известно, что радиус вписанной в него окружности равен r.
Контрольные вопросы
1. Что такое программа на С++?
2. Какая программа является линейной?
3. Какова структура программы на С++?
4. Что такое идентификатор?
5. По каким правилам создаются идентификаторы в С++?
6. Что такое тип величины?
7. Какие типы величин используются в языке С++?
8. Какие типы величин относятся к простым типам?
9. В каком диапазоне могут изменяться переменные типа int и float?
10. Как описываются переменные в С++? (Привести пример.)
11. Что такое операторные скобки? Каково их назначение?
12. Как выполняется команда присваивания?
13. Какая инструкция предназначена для вывода на экран сообщений?
14. Какая инструкция предназначена для ввода данных?
15. Что такое заголовочный файл? Приведите пример заголовочного файла.
16. Каково назначение заголовочных файлов?
17. Как сохранить программу? (Устно)
18. Как осуществить компиляцию текста программы? (Устно)
19. Как осуществить запуск программы? (Устно)
20. Как считать готовую программу с диска? (Устно)
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 1800; Нарушение авторских прав?; Мы поможем в написании вашей работы!