Понятие рекурсии

Понятие итеративного процесса

Итерация и рекурсия

Итеративный процесс можно определить как процесс вычислений, основанный на повторении последовательности операций, при котором на каждом шаге повторения используется результат предыдущего шага. Примерами итеративных алгоритмов могут служить алгоритмы вычисления факториала натурального числа, последовательности чисел Фибоначчи, вычисление суммы членов последовательности с заданным числом слагаемых и т.д. Итеративные процессы программируются обычно с помощью циклических конструкций.

Пример. Вычисление факториала числа n.

int factor (int n)

{

int f = 1;

for (int i = 2; i <= n; i++) f *= i;

return k;

}

В то же время повторение последовательности действий можно осуществить и другим методом, основанным на принципе возможности явного включения в конструкции языка программирования конструкции того же вида. В частности, в языке программирования C++ всякая функция может вызывать сама себя. Такой вызов называется рекурсией. Функция, вызывающая саму себя, называется рекурсивной.

Вообще алгоритм решения задачи называется рекурсивным, если он выражается в терминах решения более простой версии той же задачи и, кроме того, в нем предусмотрено решение самого простого варианта задачи.

При рекурсивном вызове функций в С++ используется стековая организация хранения локальных параметров.

Стек является простейшей динамической структурой организации данных. Добавление элементов в стек и выборка из него выполняются из одного конца, называемого вершиной стека. Говорят, что стек реализует принцип обслуживания LIFO (last in — first out, последним пришел - первым ушел (обслужен)).

Стеки широко применяются в системном программном обеспечении, компиляторах, в различных рекурсивных алгоритмах.

Различия между итерацией и рекурсией:

1) итерации необходим цикл и вспомогательные величины, в то время как рекурсия обходится без вспомогательных величин и обычно проще для понимания, короче и нагляднее итерации;

2) итерация требует меньше места в оперативной памяти именьших затрат машинного времени, чем рекурсия, которой необходимы затраты на управление стеком;

3) при реализации рекурсии велика вероятность переполнения стека.

Поэтому при выборе способа описания функции следует вначале решить, чему отдать предпочтение – эффективности программы или ее компактности. Однако следует избегать рекурсий там, где есть очевидное итерационное решение. Вместе с тем существует много хороших примеров применения рекурсии (построение графических образов разнообразных узоров, работа с двоичными деревьями).

При рекурсивном описании функции последняя всегда должна содержать, по крайней мере, одну альтернативную нерекурсивную ветвь алгоритма с условием окончания вычислений, заканчивающуюся оператором возврата результата.

Различают две формы рекурсивных подпрограмм:

- прямая рекурсия;

- косвенная рекурсия.

В первом случае функция содержит вызов этой же функции.

Косвенная рекурсия возникает в том случае, когда две или более функций вызывают друг друга. В случае двух функций: некоторая функция обращается к другой функции, а та в свою очередь вызывает первоначальную функцию. Для предотвращения зацикливания одна или обе функции должны проверять условие завершения.

Пример: Составить рекурсивную функцию, вычисляющую факториал числа n по формуле (учесть, что 0! = 1):

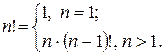
long fact (long n)

{

if (n==0 || n == 1) return 1;

return (n*fact(n-l));

}

То же самое можно записать короче:

long fact (long n)

{

return (n > 1)? n*fact(n-l): 1;

}

Пример: Распечатать последовательность, состоящую из n букв А и n букв В.

void abn (int n){

cout<<”A”;

if (n > 1) abn(n-l);

cout<<”B”;

return

}

Лабораторная работа №6
Программирование рекурсивных алгоритмов

ЦЕЛЬ РАБОТЫ: закрепление навыков программирования с использованием рекурсивных функций.

Выполнение работы: в соответствии с вариантом, используя прямую рекурсию,составить и реализовать программу.

Задание

1. Описать рекурсивную функцию NOD(A, B) целого типа, находящую наибольший общий делитель (НОД) двух целых положительных чисел A и B, используя алгоритм Евклида: НОД(A, B) = НОД(B, A mod B), если B ≠ 0; НОД(A, 0) = A. С помощью этой функции найти НОД(A, B), НОД(A, C), НОД(A, D), если даны числа A, B, C, D.

2. Для n = 12 найти числа Фибоначчи. Числа Фибоначчи: F(0) = 1, F(1) = 1 F(n) = F(n - 2) + F(n - l)

3. Даны целые числа m и n, где 0 ≤ m ≤ n, вычислить, используя рекурсию, число сочетаний С(n, m) по формуле: , 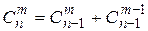при 0 ≤ m ≤ n. Воспользовавшись формулой можно проверить правильность результата.

4. Опишите рекурсивную функцию, которая по заданным вещественному х и целому п вычисляет величину хⁿ согласно формуле:

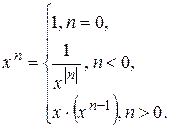
5. Задана последовательность положительных чисел, признаком конца которых служит отрицательное число. Используя рекурсию, подсчитать количество чисел и их сумму.

6. Напишите рекурсивную функцию K (n), которая возвращает количество цифр в заданном натуральном числе n, используя формулу:

7. Определим функцию S (n), вычисляющую сумму цифр заданного натурального числа:

Описать рекурсивную функцию DigitSum(K) целого типа, которая находит сумму цифр целого числа K, не используя оператор цикла. С помощью этой функции найти суммы цифр для пяти данных целых чисел.

8. Дан вектор X из n вещественных чисел. Найти минимальный элемент вектора, используя вспомогательную рекурсивную функцию, находящую минимум среди последних элементов вектора X, начиная с n -гo.

9. Напишите рекурсивную функцию для нахождения биномиальных коэффициентов (для заданного М ≥ i ≥ j > 0 вычислите все ):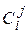

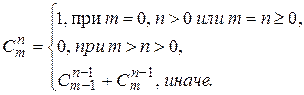
10. Напишите программу вычисления функции Аккермана для всех неотрицательных целых аргументов т и п:

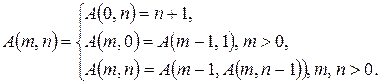
11. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

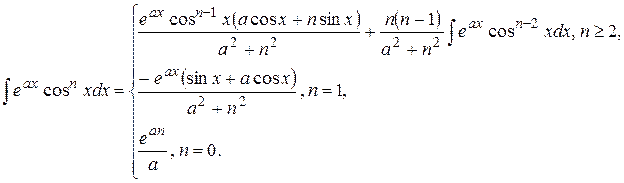
12. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

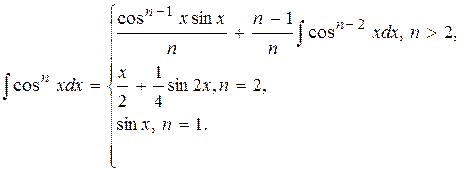
13. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

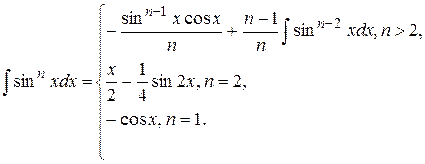
14. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

15. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

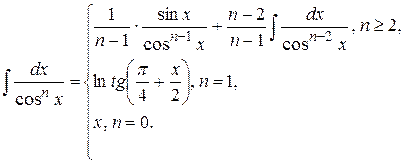
16. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

17. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

18. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

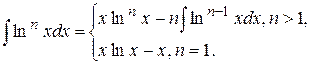
19. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

20. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

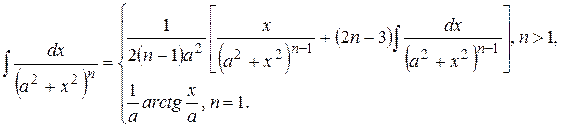
21. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

22. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

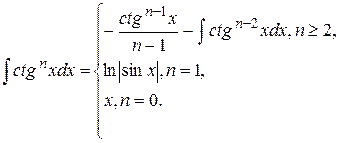
23. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

24. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:

25. Напишите рекурсивную функцию, перемножающую два целых числа, одно из которых неотрицательно, без использования операции умножения.

Контрольные вопросы

1. Какой процесс называется итеративным?

2. Каким образом реализуются итеративные процессы?

3. Какой алгоритм называется рекурсивным?

4. Какая функция называется прямо рекурсивной? Косвенно рекурсивной?

5. Что такое стек? В какой последовательности происходит заполнение стека и выбор элементов из стека?

6. Что должно обязательно присутствовать в теле рекурсивно описанной функции?

7. Перечислите различия между итерацией и рекурсией.

8. Что произойдет, если рекурсивный алгоритм будет вызывать сам себя «бесконечное» число раз?

9. Как предотвратить бесконечное выполнение рекурсивного алгоритма?

10. Верно ли, что решение задачи, реализуемое рекурсивным алгоритмом, можно выразить, используя итерацию?

Дата добавления: 2014-11-16