Максимальные напряжения при кручении

Из формулы для определения напряжений и эпюры распределе­ния касательных напряжений при кручении видно, что максималь­ные напряжения возникают на поверхности.

Определим максимальное напряжение, учитывая, что ρ_{та х} = d/ 2, где d — диаметр бруса круглого сечения.

Для круглого сечения полярный момент инерции рассчитывает­ся по формуле (см. лекцию 25).

Максимальное напряжение возникает на поверхности, поэтому имеем

Обычно J_P/p_max обозначают W_p и называют моментом сопро­тивления при кручении, или полярным моментом сопротивления сечения

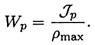
Таким образом, для расчета максимального напряжения на поверхности круглого бруса получаем формулу

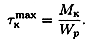
Для круглого сечения

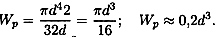
Для кольцевого сечения

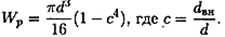
Условие прочности при кручении

Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности

где [ τ _к] — допускаемое напряжение кручения.

Дата добавления: 2014-11-18