Пределы применимости формулы Эйлера. Критические напряжения

Критические напряжения.

Критическое напряжение — напряжение сжатия, соответству­ющее критической силе.

Напряжение от сжимающей силы определяется по формуле

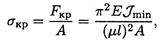
где σ_кр — напряжение сжатия, при котором стержень еще устойчив. Корень квадратный из отношения минимального момента инерции сечения к площади поперечного сечения принято называть мини­мальным радиусом инерции i_т;_п:

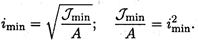
Тогда формула для расчета критического напряжения перепи­шется в виде

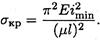
Отношение μl/i _min носит название гибкости стержня λ.

Гибкость стержня — величина безразмерная, чем больше гиб­кость, тем меньше напряжение:

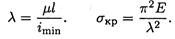
Заметим, что гибкость не зависит от материала, а определяется только геометрией стержня.

Формула Эйлера выполняется только в пределах упругих де­формаций.

Таким образом, критическое напряжение должно быть меньше предела упругости материала.

Предел упругости при расчетах можно заменять пределом про­порциональности. Таким образом, σ _кр ≤ σ _у ≈ σ_пц, где σ _у — предел упругости; σ_ПЦ — предел пропорциональности материала;

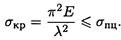
Откуда гибкость стержня:

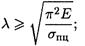
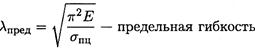
Предельная гибкость зависит от материала стержня.

В случае, если λ < λ _пред в материале стержня возникают оста­точные деформации. Поскольку в реальных конструкциях могут воз­никать пластические деформации, не приводящие к потере работо­способности, созданы эмпирические формулы для расчетов в этих случаях.

Дата добавления: 2014-11-18