Обработка и анализ результатов измерений

1. Цель работы: изучение методов измерения физических величин, практических приемов обработки и анализа результатов измерений. Изучение нониусов.

2. Краткая теория

Методы измерения физических величин. Погрешности измерений

Измерение в широком смысле слова — это операция, посредством которой устанавливается численное соотношение между измеряемой величиной и заранее выбранной мерой. Мы будем рассматривать измерение физических величин.

Физическая величина — это свойство, общее в качественном отношении многим объектам (физическим системам, их состояниям и происходящим в них процессам), но в количественном отношении — индивидуальное для каждого физического объекта.

Измерить физическую величину — это значит сравнить её с другой, однородной величиной, принятой за единицу измерения.

Для измерения физических величин применяются различные технические средства, специально для этого предназначенные и имеющие нормированные метрологические свойства.

Поясним некоторые из указанных средств измерений.

Мера — это средство измерений в виде тела или устройства, предназначенного для воспроизведения величин одного или нескольких размеров, значения которых известны с необходимой для измерений точностью. Примером меры могут служить гиря, измерительная колба, масштабная линейка.

В отличие от меры измерительный прибор не воспроизводит известное значение величины. Измеряемая величина в нём преобразуется в показание или сигнал, пропорциональный измеряемой величине в форме, доступной для непосредственного воспроизведения. Примером измерительного прибора могут слу­жить амперметр, вольтметр, термопара и пр.

Измерения физических величин могут отличаться друг от друга особенностями технического или методического характера. С методической точки зрения измерения физических величин поддаются определённой систематизации. Их можно, например, подразделять на прямые и косвенные.

Если измеряемая величина непосредственно сравнивается с соответствующей единицей её измерения или определяется путём отсчёта показаний измерительного прибора, градуированного в соответственных единицах, то такое измерение называется прямым. Например, измерения толщины проволоки микрометром, промежутка времени секундомером, силы тока амперметром — являются прямыми.

Большинство физических величин измеряется косвенным путём. Косвенным называется такое измерение, при котором искомая физическая величина непосредственно не измеряется, а вычисляется по результатам прямых измерений некоторых вспомогательных величин, связанных с искомой величиной определённой функциональной зависимостью.

При любых измерениях физических величин получаются результаты, которые неизбежно содержат погрешности (ошибки). Эти погрешности обусловлены самыми разнообразными причинами (несовершенство мер и измерительных приборов, несовершенство наших чувств). Результаты измерений являются, поэтому лишь приближёнными, более или менее близкими к истинным значениям измеряемых величин.

Разность между истинным значением измеряемой величины х и фактически измеренным 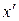называется истинной абсолютной погрешностью, или ошибкой измерения:

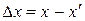(1)

Отношение истинной абсолютной погрешности к истинному значению измеряемой величины х называется истинной относительной погрешностью измерения:

. (2)

Относительная погрешность — величина отвлечённая, она выражается в долях единицы или в процентах и поэтому позволяет сравнивать точность независимых друг от друга выполненных измерений (например, точность измерения диаметра и высоты цилиндра).

Так как никакое измерение не может дать истинного значения измеряемой величины, то задачей измерения любой физической величины является нахождение приближённого наиболее вероятного значения этой величины, а также определение и оценка допущенной при этом погрешности.

Погрешности (ошибки), которые имеют место при измерении физических величин, подразделяются на три группы: грубые, систематические, случайные. Грубые ошибки (промахи)— это ошибки, явно искажающие результаты измерений. Причинами грубых ошибок могут быть неисправности эксперимен­тальной установки или измерительного прибора. Но чаще всего это следствие ошибок самого экспериментатора: неправильное определение цены деления измерительного прибора, неверный отсчёт делений, но шкале прибора, ошибочная запись результатов прямых измерений и т. п. В дальнейшем изложении, будем предполагать, что измерения не содержат грубых ошибок (промахов).

Систематические погрешности обусловлены действием постоянных по величине и направлению факторов. Например, неточностью изготовления мер, неправильной градуировкой шкал или неправильной установкой измерительных приборов, а также постоянным и односторонним воздействием на измеряемую величину или измерительную установку какого-либо внешнего фактора.

При повторных измерениях данной величины в одинаковых условиях систематическая погрешность каждый раз повторяется, имея одну и ту же величину и знак, или изменяется по определённому закону. При внимательном анализе принципа действия применяемых приборов, методики измерения и окружающих условий, систематические погрешности можно либо исключить в самом процессе измерения, либо учесть в окончательном результате измерений, внеся соответствующую поправку.

Случайные погрешности обусловлены действием большого числа самых разнообразных, как правило, переменных факторов, в своём большинстве не поддающихся учёту и контролю и проявляющихся в каждом отдельном измерении по-разному. В силу неупорядоченности совокупного действия этих факторов предвидеть появление случайной погрешности и предугадать её величину и знак невозможно. Погрешность такого рода потому и называется случайной, что появление её — дело случая, появление её не вытекает из данных условий эксперимента. Она может быть, а может и не быть.

Случайные погрешности проявляют себя в том, что при не­изменных условиях эксперимента и при полностью исключённых систематических погрешностях результаты повторных измерений одной и тон же величины оказываются несколько отличающимися друг от друга. Случайные погрешности, по указанным выше причинам не могут быть исключены из результатов измерений, как, например, погрешности систематические.

3акон распределения случайных погрешностей

Полностью избежать или исключить совершенно случайные погрешности невозможно, так как факторы, их вызывающие, не поддаются учёту и носят случайный характер. Возникает вопрос: как уменьшить влияние случайных погрешностей на окончательный результат измерения и как оценить точность и достоверность последнего? Ответ на этот вопрос даёт теория вероятностей. Теория вероятностей — это математическая наука, выясняющая закономерности случайных событий (явлений), которые проявляются при действии большого числа случайных факторов.

Случайные погрешности измерений относятся к группе не­прерывных величин. Непрерывные величины характеризуются бесчисленным множеством возможных значений. Вероятность любого значения непрерывной случайной величины бесконечно мала. Поэтому, чтобы выявить распределение вероятностей для какой-то непрерывной случайной величины, например, величины 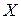, рассматривают ряд интервалов значений этой величины и подсчитывают частоты попадания значений величины 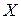в каждый интервал . Таблица, в которой приведены интервалы в порядке их распределения вдоль оси абсцисс и соответствующие им частоты, называется статистическим рядом (табл. 1).

Таблица 1

Интервалы I			.......		.......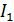
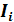
Частоты Р*			.......		.......

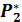
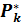
Статистический ряд графически представляется в виде ступенчатой кривой, которую называют гистограммой. При построении гистограммы по оси абсцисс откладываются интервалы возможных значений случайной величины, а по оси ординат — частоты или число случаев, когда значение случайной величины попадает в данный интервал. Для большинства интересующих нас случайных погрешностей гистограмма имеет вид, показанный на рис. 1. На этом рисунке высота, а следовательно, и площадь прямоугольника для каждого интервала ошибок пропорциональны числу опытов, в которых данная ошибка наблюдалась.

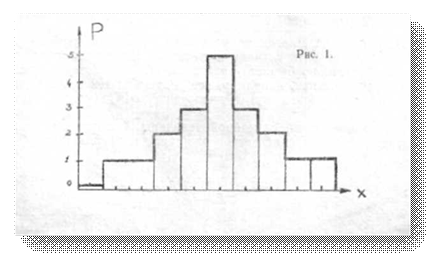При увеличении числа опытов (измерений) и уменьшении интервала разбиения оси абсцисс гистограмма теряет свой ступенчатый характер и стремится (переходит) к плавной кривой (рис. 2). Такую кривую называют кривой плотности распределения для данной случайной величины, а уравнение, описывающее эту кривую, называется законом распределения случайной величины.

Считается, что случайная величина полностью определена, если известен закон её распределения. Этот закон может быть представлен (задан) в интегральной или дифференциальной форме. Интегральный закон распределения случайной величины обозначается символом 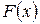и называется функцией распределения. Производная функция от 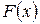называется плотностью вероятности случайной величины X или дифференциальным законом распределения:

.

При решении многих практических задач нет необходимости характеризовать случайную величину исчерпывающим образом. Достаточно бывает указать только её некоторые числовые характеристики, например, её математическое ожидание 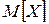(можно писать 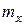) и дисперсию 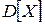(можно писать ).

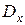Для непрерывной случайной величины X с плотностью вероятности 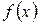математическое ожидание вычисляется по формуле

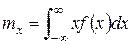. (3)

Для непрерывной случайной величины X дисперсия определяется по формуле:

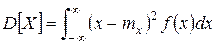. (4)

Положительный квадратный корень из дисперсии обозначается символом 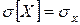и называется средним квадратическим отклонением (сокращенно с. к. о.):

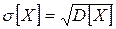. (5)

При конечном числе опытов 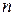в качестве оценки 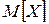принимают среднее арифметическое наблюденных (измеренных) значений 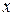, т. е.

. (6)

Для оценки дисперсии (с. к. о.) используют формулу

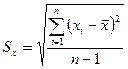. (7)

Следует иметь в виду, что среднее арифметическое случайной величины 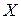само является случайной величиной, так как вычисляется на основании ограниченного числа опытов. Разброс значений величины 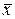характеризуют средним квадратическим отклонением , которое связало с упомянутым выше 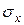соотношением:

. (8)

При ограниченном числе опытов в качестве оценки принимают отношение

. (9)

Согласно закону больших чисел все три оценки при увеличении числа опытов приближаются (сходятся по вероятности) соответственно к и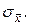

Практика обработки статистических данных показывает, что числовые характеристики случайной величины ( 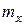и 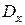) существенно зависят от вида предполагаемого закона распределения рассматриваемой случайной величины.

Предельная кривая, к которой в большинстве случаев стремятся гистограммы случайных погрешностей измерений физических величин при неограниченном увеличении числа опытов, имеет колоколообразный вид и называется кривой Гаусса (рис. 2). Аналитическое выражение этой кривой называется законом распределения Гаусса или законом нормального распределения. Для случайной величины 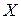этот закон можно записать в виде:

. (10)

где 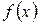— плотность вероятност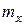и; и 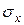— математическое ожидание и среднее квадратическое отклонение — параметры нормального распределения, физический смысл и способ вычисления которых были пояснены выше.

При рассмотрении свойств и характеристик распределения случайных погрешностей мы ограничимся только нормальным законом, так как случайные погрешности измерений чаще всего распределяются нормально (по закону Гаусса). Это означает:

1) случайная погрешность измерения может принимать любые значения в интервале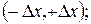

2) случайные погрешности, равные по абсолютной величине, но противоположные по знаку, равновероятны, то есть встречаются одинаково часто;

3) чембольше по абсолютной величине случайные погрешности, тем они менее вероятны, то есть встречаются реже.

Дата добавления: 2014-11-08