Основные операции с матрицами 1 страница

Сложение двух матриц	Умножение матрицы на скаляр
Складывать матрицы можно только при условии, что они имеют одинаковый размер. Чтобы сложить две матрицы, нужно сложить все их соответствующие элементы.	Скаляр представляет собой константу. Чтобы умножить матрицу на скаляр, нужно умножить на скаляр каждый элемент этой матрицы.

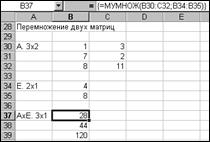
Перемножение двух матриц. Две матрицы можно перемножить при условии, что количество столбцов первой матрицы равно количеству строк второй матрицы. Перед умножением следует указать, где будет находиться результирующая матрица (следует указывать реальный размер с правильным количеством ячеек; если размеры матриц заранее неизвестны, лучше выбрать слишком большой диапазон, чем слишком маленький). После указания местоположения новой матрицы, можно ввести функцию массива МУМНОЖ (матрица1; матрица2), выполняющую перемножение матриц, указывая диапазоны матриц с помощью мыши. Чтобы закончить ввод формулы следует нажать комбинацию клавиш Ctrl+Shift+Enter, тогда функция перемножения матриц будет введена во все ячейки матрицы-произведения.

Транспонирование матриц с помощью функции ТРАНСП (). Необходимо:

Ø Ввести исходную матрицу.

Ø Указать диапазон ячеек соответствующего размера, куда нужно поместить результат.

Ø Ввести функцию массива ТРАНСП(матрица), указав с помощью мыши диапазон ячеек, содержащих исходную матрицу.

Ø Ввод завершить комбинацией клавиш Ctrl+Shift+Enter.

Обращение матриц. Операция применима только к квадратным матрицам. Кроме того, она должна быть несингулярной. Необходимо:

Ø Ввести исходную матрицу.

Ø Указать место для размещения обратной матрицы и ее правильный размер (он совпадает с размером исходной матрицы).

Ø Ввести функцию массива МОБР(матрица), указав с помощью мыши диапазон ячеек, содержащих исходную матрицу.

Ø Ввод завершить комбинацией клавиш Ctrl+Shift+Enter.

Вычисление детерминанта матрицы. Детерминант матрицы - это скалярная величина, которая определяется только для квадратных матриц. Часто используется для решения системы линейных уравнений, для определения сингулярности матрицы. Если детерминант матрицы равен 0, то система уравнений не имеет решения, а матрица сингулярная. Для вычисления детерминанта используется функция массива МОПРЕД(матрица).

Использования функций поиска для поиска значений в таблицах и связи между таблицами.

Электронные таблицы предоставляют возможность организации справочников (вспомогательных таблиц), позволяющих по коду некоторого объекта получить значения одного из нескольких сопоставляемых этому объекту параметров.

Справочник (вспомогательная таблица) представляет собой прямоугольный фрагмент, левая колонка или верхняя строка которого содержат коды, используемые для поиска нужных сведений. В первом случае справочник называется вертикальным, во втором - горизонтальным. Иногда справочник может быть частью той же таблицы, в которую добавляются найденные параметры. Справочники являются типичными примерами табличных документов, которые удобно реализовывать в среде электронных таблиц.

Для решения подобного рода задач используются функции ВПР (Вертикальный ПРосмотр) и ГПР (Горизонтальный ПРосмотр).

Имя функции	Действие
ВПР (значение; массив; n; диапазон просмотра)	Осуществляет поиск значения в первом столбце массива и возвращает значение из той же строки и n-го столбца
ГПР (значение; массив; n; диапазон просмотра)	Осуществляет поиск значения в верхней строке массива и возвращает значение из того же столбца и n-ой строки

Замечание. Если логический аргумент «диапазон просмотра» имеет значение ЛОЖЬ, совпадение должно быть точным; если этот аргумент имеет значение ИСТИНА, из всех значений таблицы используется то, которое подходит лучше других.

Вызов функции с помощью Мастера функций, окно которого можно вызвать с помощью кнопки на панели инструментов.

В появившемся окне функции ВПР указываются ссылки на ячейки, в которых находятся значения для четырех параметров:

1. Искомое значение – то, что нужно найти в первом столбце справочника (марка самолета);

2. Табл. массив – место расположения справочника, в котором осуществляется поиск;

3. Номер индекса столбца – столбец справочника, в котором будет осуществляться поиск (назначение самолета);

4. Диапазон просмотра – логическая величина, определяющая, точно (ИСТИНА) или приближенно (ЛОЖЬ) должно производиться сравнение.

Следует обратить внимание, что ссылка на диапазон месторасположения справочника должна быть абсолютной. Значит в ячейку Е15 будет введена формула =ВПР(A15;$A$3:$E$10;2;ИСТИНА)

Пример использования функции ВПР при выборе назначения самолета по справочнику типов.

Аналитические методы обработки числовых данных.

Обработка числовых данных с помощью компьютера позволяет производить сложные, объемные расчеты, за короткое время и обеспечить при этом высокую точность и надежность вычислений.

Большинство математических систем, используемых при работе с компьютерами, являются системами для выполнения численных расчетов, т.е. численными системами. Они превращают компьютер в большой программируемый калькулятор, способный быстро и автоматически (по введенной программе) выполнять арифметические операции. Их результат всегда конкретен – это или числа, или совокупности чисел.

Однако, бывают случаи, когда характер самой задачи не даёт возможности решить её численными методами (например, вычисление суммы числового ряда, являющегося расходящимся), т.е. возникает необходимость получить решение задачи в символьном (аналитическом) виде. Кроме того, очень часто даже самая мизерная ошибка вычислений сильно искажает результат. Если разрешить в последовательных шагах вычислений переменным оставаться неизвестными (т.е. без числовых значений) и в точной форме (например, 1 / 3 вместо 0,3333…), можно обеспечить получение ответов с гораздо большей точностью и избежать ошибки округлений.

Для решения подобных задач в качестве альтернативы численным методам используют символьную компьютерную математику и соответственно символьные математические системы. Подобные системы позволяют также осуществлять такие распространенные аналитические вычисления как упрощение математических формул, вычисление пределов, производных и первообразных функций, разложение их в ряды Тейлора и Фурье, вычисление корней многочленов с буквенными коэффициентами и т.д. и т.п.

Освоение символьной математики компьютерами началось в начале 60-х годов. В связи с этим появилось новое научное направление – компьютерная алгебра.

В настоящее время для научно-технических расчетов на компьютерах все чаще и чаще используется не традиционные языки программирования и не электронные таблицы, а специальные математические программы типа Reduce, Eureka и такие мощные математические пакеты для персональных компьютеров как Derive, Mathematica, Maple MathCAD, MatLab.

Математические пакеты как инструмент обработки числовых данных. Универсальные математические пакеты предназначены для проведения разнообразных математических вычислений – аналитических (символьных) или приближенных (численных). Помимо универсальных, говорят о специализированных математических пакетах, которые предназначены для решения математических задач вполне определенного круга. Например, статистические пакеты решают задачи анализа данных методами математической статистики.

Все математические пакеты позволяют выполнять арифметические и логические операции, производить вычисление алгебраических, тригонометрических функций и им обратных; выполнять статистические и финансово-экономические операции. Действия могут выполняться над числами произвольной разрядности и в различных системах счисления (от 2 до 36), с действительными и комплексными числами. Имеется обширный набор средств для работы с матрицами. Полученные при вычислении результаты в математических пакетах могут интерпретироваться в графическом виде. Современные математические пакеты содержат встроенные средства вычерчивания плоских и трехмерных графиков.

Особенности современных математических пакетов (MathCad, Mathematica и Maple). Все математические пакеты имеют общий и хорошо известный из опыта работы с текстовыми и графическими редакторами интерфейс, знакомый набор файловых операций, известные принципы редактирования документов, возможности настройки системы.

Математические выражения записываются в их общепринятой нотации: числитель находится вверху, а знаменатель – внизу; в интеграле пределы интегрирования также расположены на своих привычных местах.

Основной особенностью всех современных математических систем является то, что они обладают средствами символьной математики, что позволяет решать поставленные задачи или этапы задачи не только численно, но и аналитически.

Процесс создания «программы» идет параллельно с её отладкой. Это означает, что пользователь, общается с математическим пакетом в диалоговом режиме: введя в документ новое выражение, может не только сразу подсчитать, чему оно равно при определенных значениях переменных, но и построить график или поверхность, беглый взгляд на которые может безошибочно показать, где кроется ошибка, если она была допущена при вводе формул или при создании самой математической модели.

В этих пакетах имеется довольно мощный математический аппарат, позволяющий решать алгебраические уравнения и их системы (линейные и нелинейные), обыкновенные дифференциальные уравнения и системы (задача Коши и краевая задача), дифференциальные уравнения в частных производных, обрабатывать статистические данные, решать задачи интерполяции, экстраполяции, аппроксимации, работать с векторами и матрицами, исследовать функции и многое другое.

Пакеты дополнены справочником по основным математическим и физико-математическим формулам и константам, которые можно автоматически переносить в документ без опасения внести в них искажения, нередкие при ручной работе.

Как правило, к данным пакетам можно приобрести те или иные электронные учебники по различным дисциплинам: решение обыкновенных дифференциальных уравнений, статистика, термодинамика, теория управления, сопротивление материалов и т.д.;

Решая поставленную задачу, пользователь может вводить не только числовые значения переменных, но и дополнять их размерностями. При этом пользователь вправе выбирать нужную систему единиц измерения.

Современные математические системы оборудованы средствами анимации, что позволяет реализовать созданные модели не только в статике (числа, таблицы, графики), но и в динамике (анимационные клипы, построение динамических моделей исследуемых систем).

Не выходя из среды пакета, возможно, открывать новые документы на других серверах и пользоваться теми преимуществами информационных технологий, какие предоставляет Интернет.

Кроме того, не следует забывать, что современные математические системы - это полноценное Windows-приложения. Решая поставленную задачу, можно в статике (через буфер обмена Windows) или в динамике (OLE-технологии) передать данные в среду другой программы (в среду языка Pascal, например) и там решить часть задачи.

Обзор некоторых математических пакетов. Прежде чем выбрать нужный вам пакет необходимо оценить его возможности с точки зрения эффективности решаемой задачи. Ниже приводится краткая характеристика наиболее известных математических пакетов:

Derive. Этот математический пакет интересен, поскольку в нем имеется возможность использования символьной математики и двух режимов работы с графикой. Наличие графического курсора позволяет определять координаты характерных точек кривых (экстремумы, корни, точки пересечения с другими кривыми). Пакет Derive и поныне привлекателен своими невзыскательными требованиями к аппаратным ресурсам. Это единственный пакет, который работает даже на ЭВМ класса IBM PC XT без жесткого диска. Более того, при решении задач умеренной сложности он показала более высокое быстродействие и большую надежность решения.

Mathematica. Современный математический пакет Mathematica является мощным средством выполнения и оформления математических исследований как в символьной, так и в численной форме. Имеет встроенный язык программирования и мощные графические возможности. Выходной документ может быть подготовлен совместно с MS Word, MS Excel и т.д. По богатству и разнообразию средств высокого уровня и выполнения символьных вычислений этот пакет уникален. Возможность проводить аналитические расчеты – одно из важных достоинств программы. Mathematica умеет преобразовывать и упрощать алгебраические выражения, дифференцировать и вычислять определенные и неопределенные интегралы, разлагать функции в ряды и находить пределы и пр. Mathematica содержит большое количество эффективных алгоритмов для проведения численных расчетов. Программа решает численными методами множество задач, не поддающихся аналитическому решению. Внутренние алгоритмы, используемые программой для операций над математическими функциями, выбраны так, чтобы достичь возможно наибольшую точность. При всех его богатейших возможностях пакет имеет нестандартную входную и неудобную выходную математическую символику, неадекватное представление результатов многих операций, слабую диагностику ошибок и требует серьезных трудозатрат на освоение.

Серьезным недостатком справочной системы пакета, например, в сравнении с другими математическими пакетами, следует считать малое число описанных в ней практических примеров применения того или иного оператора или функции, а без этого работать с математическими пакетами очень трудно. Отсутствует очень полезная возможность – перенос примеров из базы данных помощи прямо в окно редактирование с возможностью их немедленного исполнения.

MapleV. Диапазон функциональных возможностей MapleV очень широк – охвачены следующие разделы: дифференциального и интегрального исчислений, линейной алгебры, дифференциальных уравнений, геометрии, статистики, теории чисел, теории групп, оптимизации, численных вычислений, финансовые функции, комбинаторика, теория графов и многие другие области математики. Двух- и трехмерная графика MapleV обеспечивает мощную научную визуализацию. Пакет MapleV имеет более 20 типов специальных графиков, а также большое количество доступных опций для настройки способов вывода на экран каждого графика. Кроме того, возможно оживление графиков – мультипликация. Пакет понимает многие специальные функции такие как: Дельта-функции, функции Дирака и др. MapleV имеет мощную справочную систему, которая включает файлы помощи для каждой команды, типа данных, конструкции языка и библиотеки. Ещё одним достоинством системы является огромное число описанных в ней практических примеров и перенос примеров из базы данных помощи прямо в окно редактирование с возможностью их немедленного исполнения. Кроме того, данное программное средство может использоваться для того, чтобы сгенерировать коды на языках типа C, LaTEX и др.

MathCad. Пакет MathCad создавался как мощный калькулятор, позволяющий легко справляться с рутинными задачами инженерной практики, такими как решение алгебраических и дифференциальных уравнений с постоянными и переменными параметрами, анализ функций, поиск их экстремумов, численное и аналитическое дифференцирование и интегрирование, вывод таблиц и графиков при анализе найденных решений.

Главным достоинством пакета являются:

Ø запись сложных математических выражений в том вид, в котором они обычно записываются на листе бумаги;

Ø простота в использовании;

Ø проведение численных и аналитических математических расчетов;

Ø возможность создания встроенными средствами высококачественных технических отчетов с таблицами, графиками, текстом в виде печатных документов; подготовка Web-страниц и публикация результатов в Интернете;

Ø ввод исходных данных и вывод результатов в текстовые файлы или файлы с базами данных в других форматах;

Ø легкость и наглядность программирования задач; возможность составлять собственные программы-функции с помощью конструкций подобных тем, что используются языками программирования (Pascal, Fortran) и использовать принципы модульного программирования для реализации вычислительных алгоритмов пользователя;

Ø получение различной справочной информации из области математики и многое другое.

MathCad не предназначен для профессиональных математиков и для программирования сложных задач.

MatLab. Пакет MatLab был создан компанией MathWorks более десяти лет назад. Его возможности постоянно расширяются, а заложенные в нем алгоритмы совершенствуются.

Спектр проблем, исследование которых может быть осуществлено при помощи MatLab, охватывает: матричный анализ, обработку сигналов и изображений, задачи математической физики, оптимизационные задачи, обработку и визуализацию данных, работу с картографическими изображениями, нейронные сети, нечеткую логику и многие другие. Специализированные средства собраны в пакеты, называемые ToolBox.

Так, например, пакет (ToolBox) Simulink предназначен для интерактивного моделирования нелинейных динамических систем, состоящих из стандартных блоков.

В MatLab реализованы классические численные алгоритмы решения уравнений, задач линейной алгебры, нахождения значений определенных интегралов, интерполяции, решения дифференциальных уравнений и систем.

MatLab обладает хорошо развитыми возможностями визуализации двумерных и трехмерных данных.

Простой встроенный язык программирования позволяет легко создавать собственные алгоритмы. Простота языка компенсируется огромным множеством функций MatLab и ToolBox.

Визуальная среда GUIDE предназначена для написания приложений с графическим интерфейсом пользователя.

Лекция 8.

Особенности разработки прикладных программ.

Основные понятия. Возможности компьютера как технической основы системы обработки данных связаны с используемым программным обеспечением (программами).

Программа (program, routine) – упорядоченная последовательность команд (инструкций) компьютера для решения задачи.

Программное обеспечение (software) – совокупность программ обработки данных и необходимых для их эксплуатации документов.

Программы предназначены для машинной реализации задач. Термины задача и приложение имеют очень широкое употребление в контексте информатики и программного обеспечения.

Задача (problem, task) – проблема, подлежащая решению.

Приложение (application) – программная реализация на компьютере решения задачи.

Таким образом, задача означает проблему, подлежащую реализации с использованием средств информационных технологий, а приложение, реализованное на компьютере решение задачи. Приложение, являясь синонимом слова «программа», считается более удачным термином и широко используется в информатике.

Термин задача употребляется также в сфере программирования, особенно в режиме мультипрограммирования (одновременного выполнения нескольких задач) и мультипроцессорной обработки (в ЭВМ имеется несколько процессоров) как единица работы вычислительной системы, требующая выделения вычислительных ресурсов (процессорного времени, основной памяти и т.п.). В данной лекции этот термин употребляется в смысле первого определения.

Существует большое разнообразие классификаций задач. С позиций специфики разработки и вида программного обеспечения будем различать 2 класса задач – технологические и функциональные.

Технологические задачи ставятся и решаются при организации технологического процесса обработки информации на компьютере. Технологические задачи являются основой для разработки сервисных средств программного обеспечения в виде утилит, сервисных программ, библиотек процедур и др., применяемых для обеспечения работоспособности компьютера, разработки других программ или обработки данных функциональных задач.

Функциональные задачи требуют решения при реализации функций управления в рамках информационных систем предметных областей. Например, управление деятельностью торгового предприятия, планирование выпуска продукции, управление перевозкой грузов и т.д. Функциональные задачи в совокупности образуют предметную область и полностью определяют ее специфику.

Предметная (прикладная) область (application domain) – совокупность связанных между собой функций, задач управления, с помощью которых достигается выполнение поставленных целей.

Процесс создания программ можно представить как последовательность действий, представленных на рис. 1.

Рис. 1. Схема процесса создания.

Постановка задачи (problem definition) - это точная формулировка решения задачи на компьютере с описанием входной и выходной информации.

Постановка задачи – обобщенный термин, который означает определенность содержательной стороны обработки данных. Постановка задачи связана с конкретизацией основных параметров ее реализации, определением источников и структурой входной и выходной информации, востребуемой пользователем.

К основным характеристикам функциональных задач, уточняемым в процессе ее формализованной постановки, относятся:

Ø Цель и назначение задачи, ее место и связи с другими задачами;

Ø Условия решения задачи с использованием средств вычислительной техники;

Ø Содержание функций обработки входной информации при решении задачи;

Ø Требования к периодичности решения задачи;

Ø Ограничения по срокам и точности выходной информации;

Ø Состав и форма представления выходной информации;

Ø Источники входной информации для решения задачи;

Ø Пользователи задачи (кто осуществляет ее решение и пользуется результатами ее решения).

Выходная информация по задаче может быть представлена в виде документов (типа листинга или машинограммы), сформированных кадров – видеограммы на экране монитора, файла базы данных, выходного сигнала устройству управления рис. 2.

Рис. 2. Схема взаимосвязи входной и выходной информации для решения задач.

Входная информация по задаче определяется как данные, поступающие на вход задачи и используемые для ее решения. Входной информацией служат первичные данные документов ручного заполнения, информация, хранимая в файлах базы данных (результаты решения других задач, нормативно-справочная информация – классификаторы, кодификаторы, справочники), входные сигналы датчиков рис. 2.

Обычно постановка задач выполняется в едином комплексе работ по созданию структуры внутримашинной базы данных, проектированию форм и маршрутов движения документов, изменению организации управления в рамках предметной области.

Алгоритм и его свойства.

Алгоритм – это система точно сформулированных правил, определяющая процесс преобразования допустимых исходных данных (входной информации) в желаемый результат (выходную информацию) за конечное число шагов.

Алгоритм решения задачи имеет ряд обязательных свойств:

Ø Дискретность – разбиение процесса обработки информации на более простые этапы (шаги выполнения), выполнение которых компьютером или человеком не вызывает затруднений.

Ø Определенность – (детерминированность) алгоритма – однозначность выполнения каждого отдельного шага преобразования информации. Эта характеристика обеспечивает однозначность результат процесса при заданных исходных данных.

Ø Результативность – конечность действий алгоритма решения задач, позволяющая получить желаемый результат при допустимых исходных данных за конечное число шагов.

Ø Массовость – пригодность алгоритма для решения определенного класса задач.

В алгоритме отражаются логика и способ формирования результатов решения с указанием необходимых расчетных формул, логических условий, соотношений для контроля достоверности выходных результатов. В алгоритме обязательно должны быть предусмотрены все ситуации, которые могут возникнуть в процессе решения комплекса задач.

Формы представления алгоритма. Существуют следующие формы представления алгоритма:

Ø словесная (текстуальная);

Ø графическая;

Ø на языках программирования.

При словесном способе записи алгоритма содержание последовательных этапов вычислений задается в произвольной форме на естественном языке. Словесная форма имеет ряд недостатков. Для достаточно сложных алгоритмов описание становится слишком громоздким и ненаглядным. Эта форма обычно используется на начальных стадиях разработки алгоритма.

Графическая форма представления алгоритмов является более компактной и наглядной. Алгоритм изображается в виде последовательности связанных между собой блоков, каждый из которых соответствует выполнению одного или нескольких операторов. Такое графическое представление называется блок-схемой алгоритма.

Условные графические обозначения символов (блоков), используемых для составления блок-схем, стандартизированы. Некоторые часто используемые обозначения приведены ниже.

Примечание: все эти блоки можно изобразить с помощью текстового процессора WORD (список “Автофигуры”).

Линии, связывающие элементы схемы, должны проводиться только по вертикали или горизонтали, параллельно линии внешней рамки схемы и подводиться к середине блока. Чтобы показать изменение направления, линии проводят с изломом в 90 градусов. На схеме может быть пересечение двух несвязанных линий потока или слияние их.

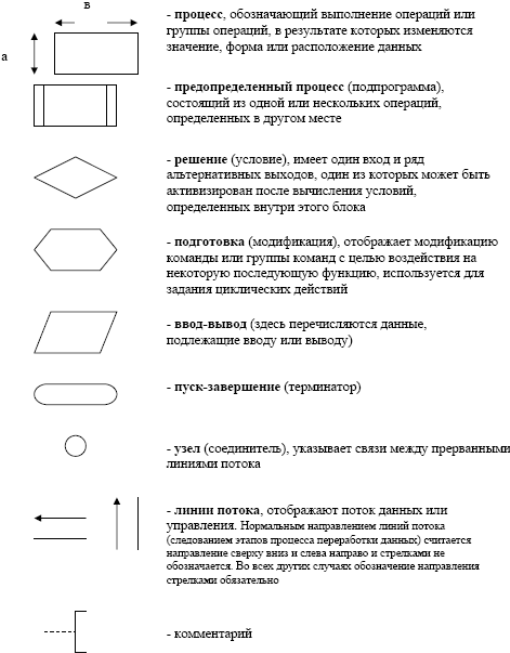
Примечание: значение а выбирается из ряда чисел 10, 15, 20 … мм; b = 1,5 a нижней граничной линий параллельно основной надписи.

Записи внутри блока должны быть представлены так, чтобы их можно было читать слева направо и сверху вниз, независимо от направления потока.

Для удобства нахождения блока на схеме, блоки можно нумеровать. Номер символа задается в виде цифр, букв или сочетания букв и цифр. Номер проставляется сверху слева в разрыве контура. Нумеруются блоки в порядке сверху вниз и слева направо.

Если содержание пояснения не помещается внутри блока, то используется “комментарий”, который может относиться как к блоку, так и к линии потока. Комментарий помещают в свободном месте схемы и соединяют с поясняемым блоком или с линией потока штриховой линией. Записывают комментарий в пределах верхней и нижней граничных линий параллельно основной надписи.

В качестве примера рассмотрим блок-схему алгоритма решения квадратного уравнения. Схема приведена на рис. 3.

Представление алгоритма в виде блок-схемы является промежуточным, так как алгоритм в таком виде не может быть выполнен на ЭВМ. Составление блок-схемы является важным и в большинстве случаев необходимым этапом решения задачи на ЭВМ, значительно облегчающим процесс составления программ.

Рис. 3. Блок-схема алгоритма решения квадратного уравнения.

Дата добавления: 2014-11-08