Расчет осветительной установки точечным методом по Айзенбергу

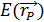Точечный излучатель. Для случая точечного излучателя, располагаемого в точке S (рис. 10), коор­динируемой вектором относительно Произвольного базиса , освещенность на расчетной по­верхности в точке Р, координируемой вектором 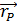от­носительно того же базиса и имеющей вектор внешней нормали определяется по формуле:

Где 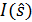- сила света излучателя S в направлении точки P, определяемом вектором:

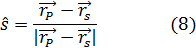
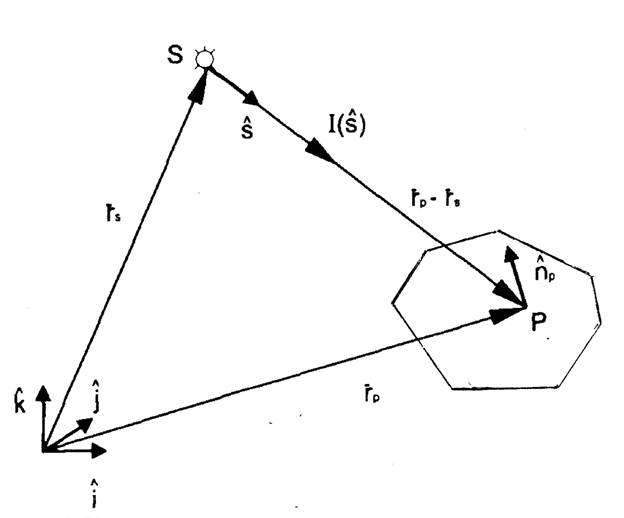Рис. 10. К расчету освещенности от точечного излучателя.

Выражение 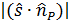представляет собой скалярное произведение векторов s и п_р. Численно равное коси­нусу угла падения луча, оно взято по модулю, так как для принятого направления вектора 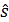(пo ходу луча) это произведение имеет отрицательное значение.

Уравнение (7) представляет собой фундаменталь­ный закон фотометрии — закон квадратов расстояний, выраженный в наиболее универсальной векторной форме.

Значение силы света 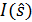определяется светораспределением излучателя и его ориентацией относительно выбранною базиса. Чтобы найти это значение, необхо­димо определить вектор 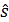в системе координат излуча­теля. Для этою удобно ввести базис излучателя 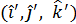связав его с направлениями его главных осей: про­дольной , поперечной 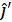и оптической 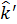(рис. 11,а),

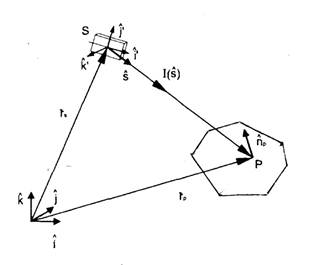
Рис. 11. (а) Расположение излучателя и объекта в сцене

В общем случае орты базиса излучателя 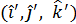удобно выразить через орты общею базиса, или базиса сцены , с помощью коэффициентов 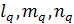(q= 1, 2, 3), представляющих собой направляющие ко­синусы осей базиса излучателя относительно общего базиса сцены:

Эти коэффициенты образуют матрицу:

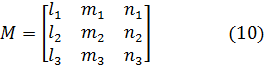
Для перевода вектора 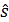базиса сцены с направляющими косинусами в вектор базиса излучателя с направляющими косинусами , тогда:

В наиболее важных практических случаях базис сцены связывается с освещаемым объектом (помещением, зданием, полотном дороги, спортивной площадкой и т.п.) так, чтобы орты 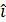, определяли горизонтальную плоскость, а орт 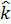- направление зенита, при этом орт базиса излучателя (продольная ось неосесимметричного СП, а следовательно, и продольная ось линейного ИС) располагается горизонтально (что имеет место в подавляющем большинстве случаев). 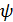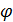При таких условиях для ориентации излучателя в сцене достаточно использовать два параметра: азимутальный угол , определяющий отклонение продольной оси излучателя (орт ) от одной из горизонтальных осей базиса сцены (например, орта ), и полярный угол , определяющий отклонение поперечной оси излучателя (орт 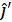) от вертикали сцены (орта 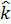) (рис.8.6,б). в этом случае матрица 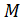принимает вид:

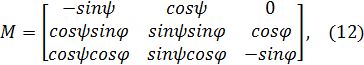
И в соответствии с (8.10) направляющие косинусы вектора равны:

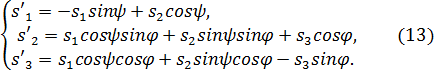
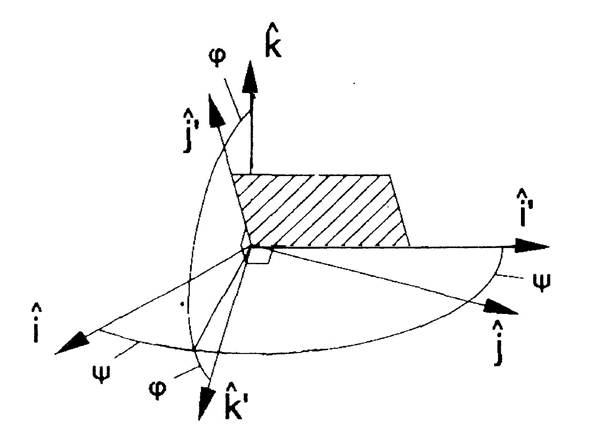
Рис. 11. (б) Ориентация базиса излучателя относительно базиса сцены. Плоскость светового отверстия излучателя заштрихована.

В зависимости от системы фотометрирования координирующие векрот углы, для которых определяется сила света 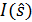, рассчитываются по следующим формулам:

- для системы (C, ) (рис. 8.7, а):

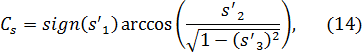
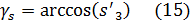
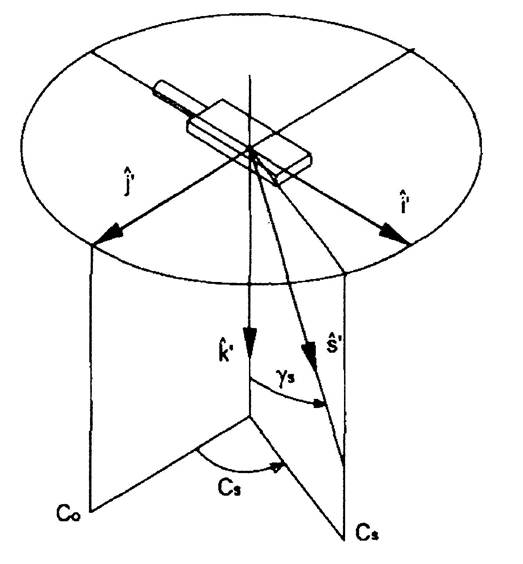
Рис. 12. (а) ориентация базиса излучателя в системе (С, γ).

- для системы (B, 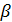) (рис. 8.7, б):

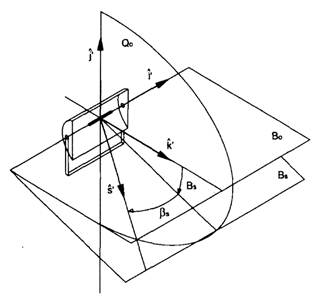
Рис. 12. (б) ориентация базиса излучателя в системе (В, β).

Для найденных углов , 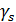или 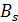, 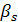непосредст­венное определение силы спета 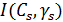или 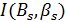осуществляется путем интерполяции исходных таблич­ных значений сил света 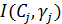или 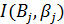, задан­ных в углax прямоугольной сетки. Выбор типа интер­поляции связан с требованиями точности расчета. Для большинства практических задач МКО рекомендует использовать линейную или квадратичную интерполя­цию [8.10]. При необходимости более высокой точно­сти может быть применена бикубическая сплайн-интерполяция [8.11]. Важным условием корректности применения нелинейных типов интерполяции является недопустимость пересечения интерполяционной кри­вой оси абсцисс, т.к. в этом случае возникают отрица­тельные значения силы света,

Линейный излучатель. Это такой излуча­тель, у которого по одному из размеров светящей по­верхности не выполняется указанный выше критерий точечности. При ручной технологии понятие линейно­го излучателя широко использовалось при расчете освещенности как от одиночною СП (например, све­тильника с ЛЛ) па близком расстоянии, так и от груп­пы СП, установленных в линию. В качестве основной характеристики светораспределения такою излучателя выступала удельная (с единицы длины) КСС, получае­мая делением реальной КСС СП либо непосредственно на его длину, либо на его длину плюс разрыв между со­седними СП при их установке в линию с разрывами. При этом КСС в продольном и поперечном сечениях аппроксимировались аналитическими функциями, что позволяло произвести интегрирование по всей линии и получить компактные и удобные для расчета аналити­ческие формулы. Понятно, что такой подход позволяет снизить трудоемкость расчета, но при этом возникают трудно оцениваемые погрешности, связанные с услов­ностью аналитической аппроксимации КСС реальных СП с учетом разрывов в линии, неоднородностью светораспределения по длине светильника.

При компьютерной технологии проблема трудоем­кости расчета таких задач снимается, и поэтому расчет от группы СП, установленных в линию, осуществляет­ся простым суммированием освешенностей от каждого СП, Так, для линии из N СП освещенность в точке 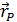равна:

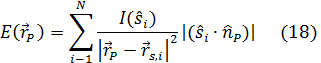
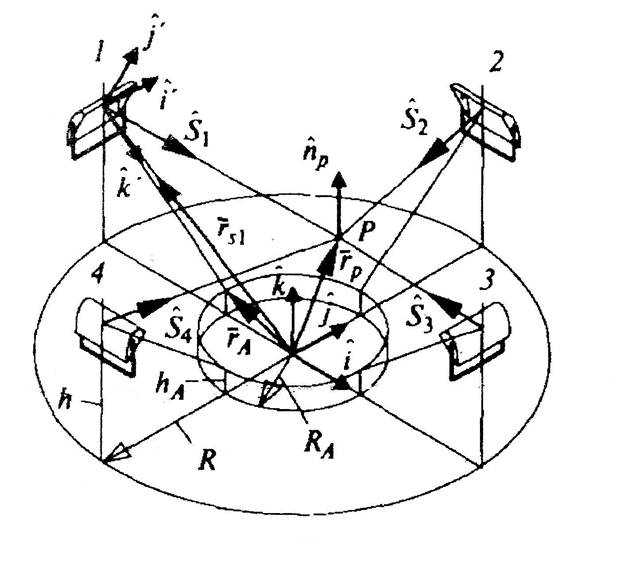
На рис. 13, а показан пример расстановки трех СП с шагом Ау по линии 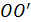,заданной вектором и ор­том 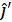. Нацеливание принято таким, что оптические оси всех СП (орты 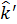) перпендикулярны линии распо­ложения световых центров излучателей 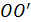и пересекают линию нацеливания 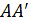заданную вектором и ортом . В этом случае орт оптической оси 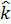равен:

а угол наклона оптической оси относительно горизон­та —

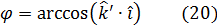
Отмстим, что для данной ориентации угол ψ =0 (рис. 11, б).

Входящий в (8.17) вектор определяется как:

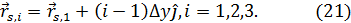
а вектор 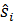, — по формуле (8.7) для соответствующего вектора

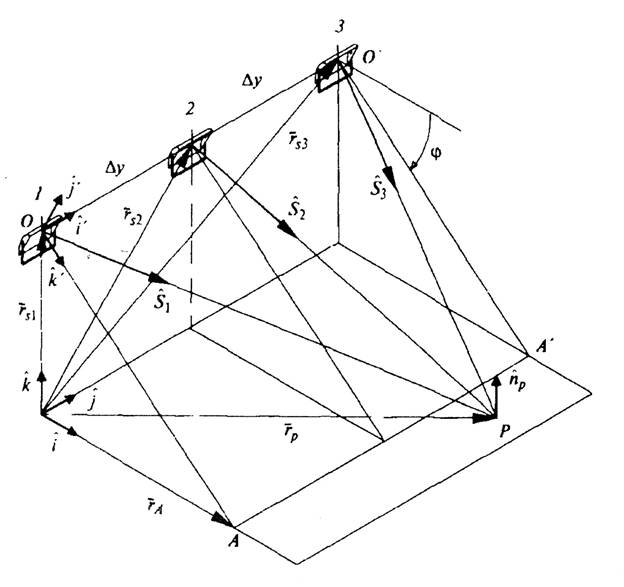
а)

б)

Рис. 13. К расчету освещенности от линейного излучателя при расположении излучателей в линию (а) и по окружности (б).

К этому же случаю относится расчет освещенности от протяженного щелевого световода. Если его светораспределение задано одной усредненной удельной (с единицы длины) КСС J_cp (C, ) [кд/м] или набором из N удельных КСС { 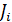(C, )}, полученных для каждо­го i -го участка оптической щели световода длиной 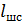, то освещенность 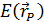в расчетной точке Р определит­ся как:

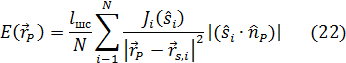
Сюда же относится случай, часто встречающийся в практике архитектурного освещения. Протяженный светильник (или группа светильников) располагается вдоль и близко от РП, например, стены. В первом при­ближении такой светильник можно представить в виле совокупности N светильников с КСС , расположенных в линию, и рассчитать освещенность на РП от таких светильников по формуле (18). Для более корректных расчетов необходимо учитывать светораспределение таких излучателей в ближней зоне (см. ниже).

Другим важным случаем является расположение СП по окружности. Показанный на рис. 13, б пример соответствует размещению четырех СП по окружности радиусом R на высоте h над РП. При этом нацеливание СП принято таким, что их оптические оси (орты 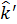) перпендикулярны этой окружности и нацелены на окружность радиусом R_A, расположенную в плоскости, параллельной РП, на высоте h_А. Для такою случая —

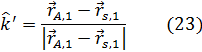
Где 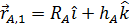, а угол наклона оптической оси 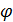относительно горизонта определяется по формуле (20) со знаком минус перед ортом 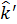. Как и в преды­дущем случае, угол ψ =0.

Поверхностный и з л у ч а т е л ь. Это такой из­лучатель, у которого по обоим размерам светящей по­верхности не выполняется критерий точечности. Как и в случае линейного излучателя, этот тип излучателя широко использовался при ручной технологии расчета. При этом большинство практических случаев базирует­ся на двух важных допущениях: излучение имеет диф­фузный (ламбертовский) характер и равномерно рас­пределено по поверхности излучателя. Это позволяет при расчетах прямого переноса излучения с одной по­верхности на другую оперировать только геометрическими параметрами: формой и размерами поверхно­стей, участвующих в таком переносе, а также их взаим­ным расположением. Влияние этих факторов учитыва­ется параметром, называемым угловым коэффициентом, определяемым как доля светового потока одной повер­хности, попавшая непосредственно на другую.

Этот показатель имеет в литературе мною разных наименований: угловой коэффициент, коэффициент использования, коэффициент связи, коэффициент формы, форм-фактор и др. В наибольшей степени терминология по данному вопросу получила развитие в теплотехнике, где различают следующие типы угловых коэффициентов [8.12]:

- элементарный, определяющий условия обмена излучением между двумя элементарными площадками;

- локальный — то же, между элементарной площад­кой и поверхностью конечных размеров;

- средний — то же. между двумя поверхностями ко­нечных размеров.

Те же коэффициенты с учетом многократных отра­жений называются разрешающими, а при наличии по­глощающей среды — обобщенными.

Угловые коэффициенты обладают рядом важных свойств, которые позволяют эффективно использовать эти параметры в практических расчетах. К таким свой­ствам относятся [8.12]:

- свойство замыкаемости, в силу которого для замкнутой системы, состоящей из N тел,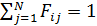

(i =1,2,… N), где — угловой коэффициент i -й по­верхности относительно j- й;

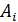- свойство взаимности, в силу которого , где и 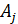— площади i -й и j -й поверхностей;

- свойство совмещаемости, в силу которого 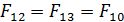, если освещаемые поверхностью по­верхности и 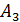имеют общую проекцию (рис. 8.9);

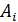- свойство распределительности, в силу которого , если поверхность состоит из двух частей: ;

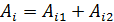-свойство затеняемости, в силу которого 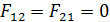, если между поверхностями 1 и 2 имеется тре­тья поверхность, препятствующая распространению излучения между ними.

На базе этих свойств были разработаны различные эффективные методы расчета угловых коэффициентов, например, алгебра угловых коэффициентов [8.13], позво­лившие решать многие практические задачи в области теплотехники и светотехники. Для большого разнооб­разия геометрических тел, их дифференциальных эле­ментов и их взаимного расположения угловые коэффициенты определены в аналитической форме и приво­дятся во многих справочных изданиях, например, [8.12], [8.14], [8.15].

Однако в компьютерной технологии используется более универсальный подход, свободный от указанных допущений и не связанный с конкретной формой и расположением излучателя. Светящая поверхность раз­бивается на совокупность элементов, для каждого из которых должен удовлетворяться критерий точечности. Такой элемент заменяется точечным излучателсм с эк­вивалентным светораспределенисм относительно цент­ра элемента. Так, если i-й элемент площадью и нормалью 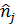; имеет распределение яркости 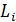(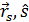), то сила света эквивалентного точечного излучателя —

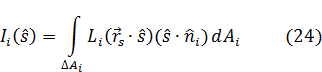
В случае однородности излучения по светящей по­верхности излучателя, т.е. 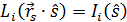(что имеет место, например, в световых потолках), выражение для силы света любого точечного излучателя может быть упрощено: 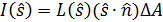. В результате освещен­ность 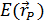в точке РП от всего поверхностного излу­чателя, замененного совокупностью N эквивалентных точечных излучателей, определяется суммированием освещенностей от всех таких точечных излучателей (см. формулу (18)).

Существует ряд задач, где допущение об однород­ности излучения по светящей поверхности некоррект­но. Сюда относится случай расчета распределения освещенности на поверхности потолка от близко рас­положенного подвесного светильника, излучающего в верхнюю полусферу. Другой важный случай относится к области архитектурного освещения, когда необходимо определить распределение освещенности на стене от близко установленного прожектора, свет которого скользит по стене. Очевидно, что здесь критерий то­чечности не выполняется, и использование в расчетах КСС приводит к большим ошибкам.

В западной литературе [8.15] подход к решению за­дачи расчета светораспределения в такой ближней зоне получил название фотометрия ближней зоны (near-field photometry), в отличие от фотометрии дальней зоны (far-fieId photometry), где критерий точечности выполня­ется, Общие подходы к решению такой задачи, базиру­ющиеся на понятии светового поля, были известны давно [8.16], [1], однако в последние годы была более четко сформулирована их практическая интерпретация. В настоящее время выделяются два основных метода для определения освещенности в ближней зоне.

В первом методе, названном фотометрией расчет­ных плоскостей (application-distance photometry), светиль­ник фотометрируется в нескольких параллельных плос­костях, расположенных перпендикулярно оптической оси светильника [8.17]. По этим данным путем интер­поляции может быть рассчитано распределение осве­щенности в любой промежуточной плоскости.

Во втором методе, названном фотометрией поля яр­кости (luminance-field photometry), выделяется массив точек окружающего СП пространства, расположенных на равном расстоянии от его светового центра, в каж­дой из которых фотометрируется индикатриса ярко­сти [8,18]. Для получения таких данных может быть использовано устройство с цифровым сканированием (CCD video camera) [8.19]. В отличие от предыдуще­го метода здесь освещенность может быть найдена не только для любого расстояния от светильника, но и при любой ориентации расчетной плоскости.

Дата добавления: 2014-11-18