
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение
|
|
|
|
КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ
«Методы оптимальных решений»
Вариант №5
Выполнил студент Нуртдинова Кристина Феликсовна,
группа 13ЭФС-101,
курс 2 заочной формы обучения
направления подготовки «Экономика»
___________________________________
(подпись)
«___» ___________ 2014г.
Научный руководитель
Ваганова Анна Сергеевна,
преподаватель
___________________________________
(подпись)
«___» ___________ 2014 г.
Челябинск 2014
Вариант 5. Для изготовления четырех видов продукции используется три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.
Таблица 1. Исходные данные.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
| А | Б | В | Г | ||
| 1 сырьё | |||||
| 2 сырьё | |||||
| 3 сырьё | |||||
| Прибыль от реализации изделия |
Задание.
1. Сформулируйте прямую оптимизационную задачу на максимум общей прибыли, рассчитайте оптимальную производственную программу, используя процедуру Поиск решения в Excel.
2. Проанализируйте использование ресурсов в оптимальном плане. Укажите статус ресурсов: дефицитный или недефицитный. Увеличение запасов какого вида ресурсов наиболее предпочтительно с точки зрения увеличения прибыли? Укажите интервалы изменения объемов используемых ресурсов, при которых сохраняются текущие оптимальные двойственные оценки. Определите, как изменится общая прибыль при увеличении запасов сырья I вида на 8 единиц.
3. Определите интервалы возможного изменения значений коэффициентов целевой функции, при которых сохраняется текущее оптимальное решение.
4. Сформулируйте двойственную задачу и найдите ее оптимальное решение, используя соотношения о дополняющей нежесткости. Сравните полученные результаты с результатами, полученными с помощью процедуры Microsoft Office Excel «Поиск решения».
Обозначим. 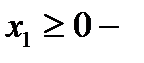 количество изделий «А»,
количество изделий «А», 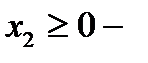 количество изделий «Б»,
количество изделий «Б», 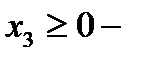 количество изделий «В»,
количество изделий «В», 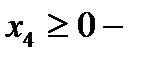 количество изделий «Г».
количество изделий «Г».
Сформулируем прямую оптимизационную задачу на максимум общей прибыли:
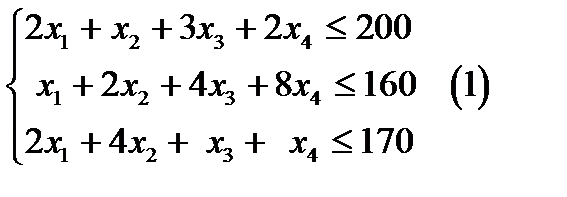 .
.
Целевая функция на максимум общей будет иметь вид:
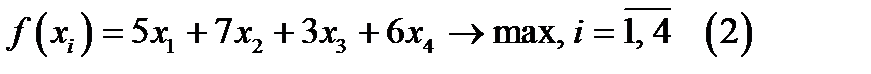 .
.
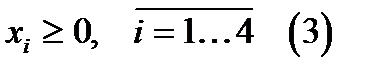 .
.
Записи (1), (2) и (3) представляют собой формальный вид прямой задачи линейного программирования на максимум общей прибыли.
Открываем книгу «Excel». Задаём имя файла «Excel» – «NO print. Вариант 5». Сохраняем созданный файл, например, «На рабочем столе». Создаём форму и заполняем её для использования встроенной функции Microsoft Office Excel «Поиск решения».
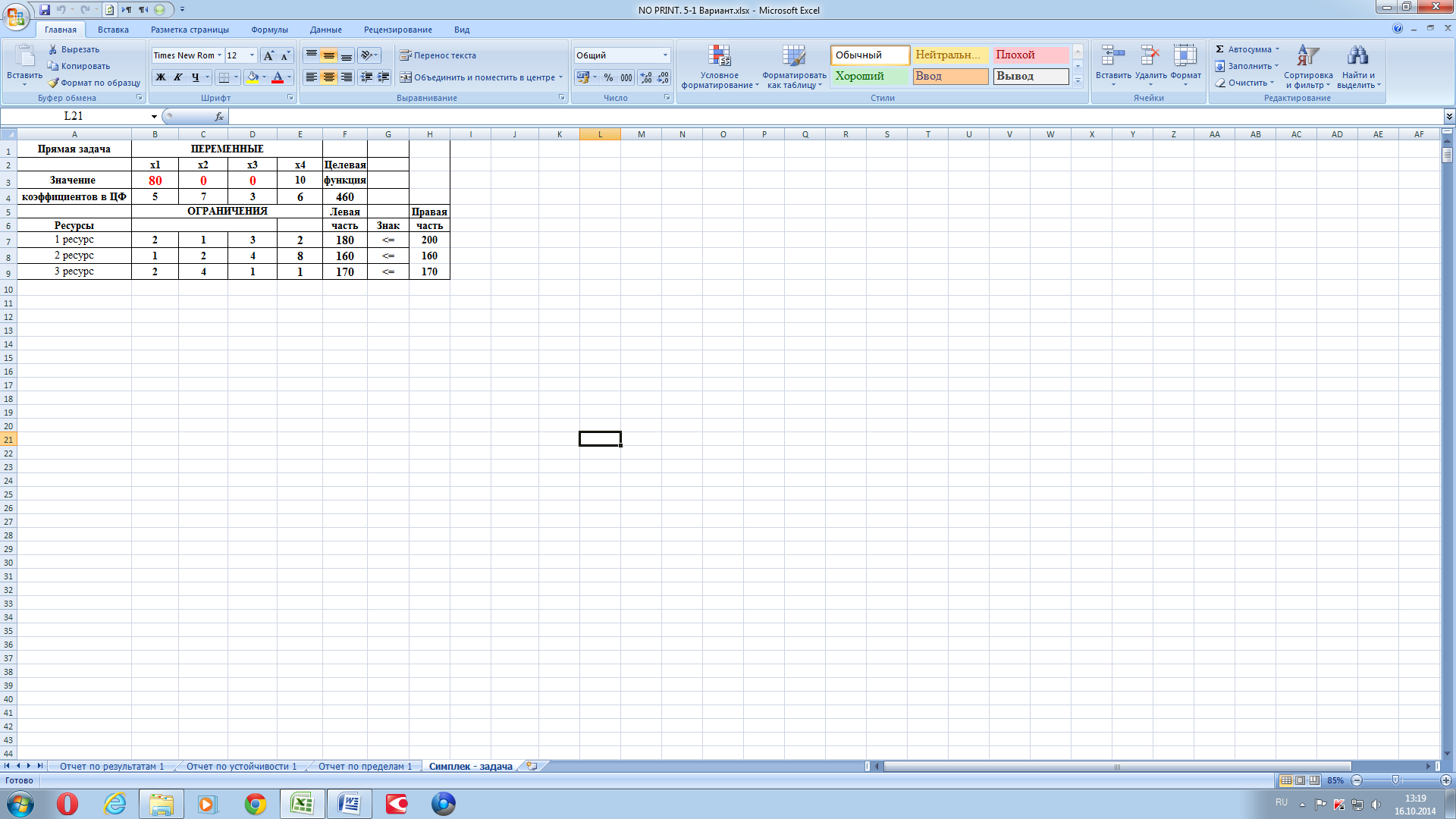
Рисунок 1.
Теперь маркер ставим в ячейку «F4». Выделяем данную ячейку. Маркер перемещаем на значок функция  . Среди «математических функций» выбираем функцию «СУММПРОИЗВЕДЕНИЯ».
. Среди «математических функций» выбираем функцию «СУММПРОИЗВЕДЕНИЯ».
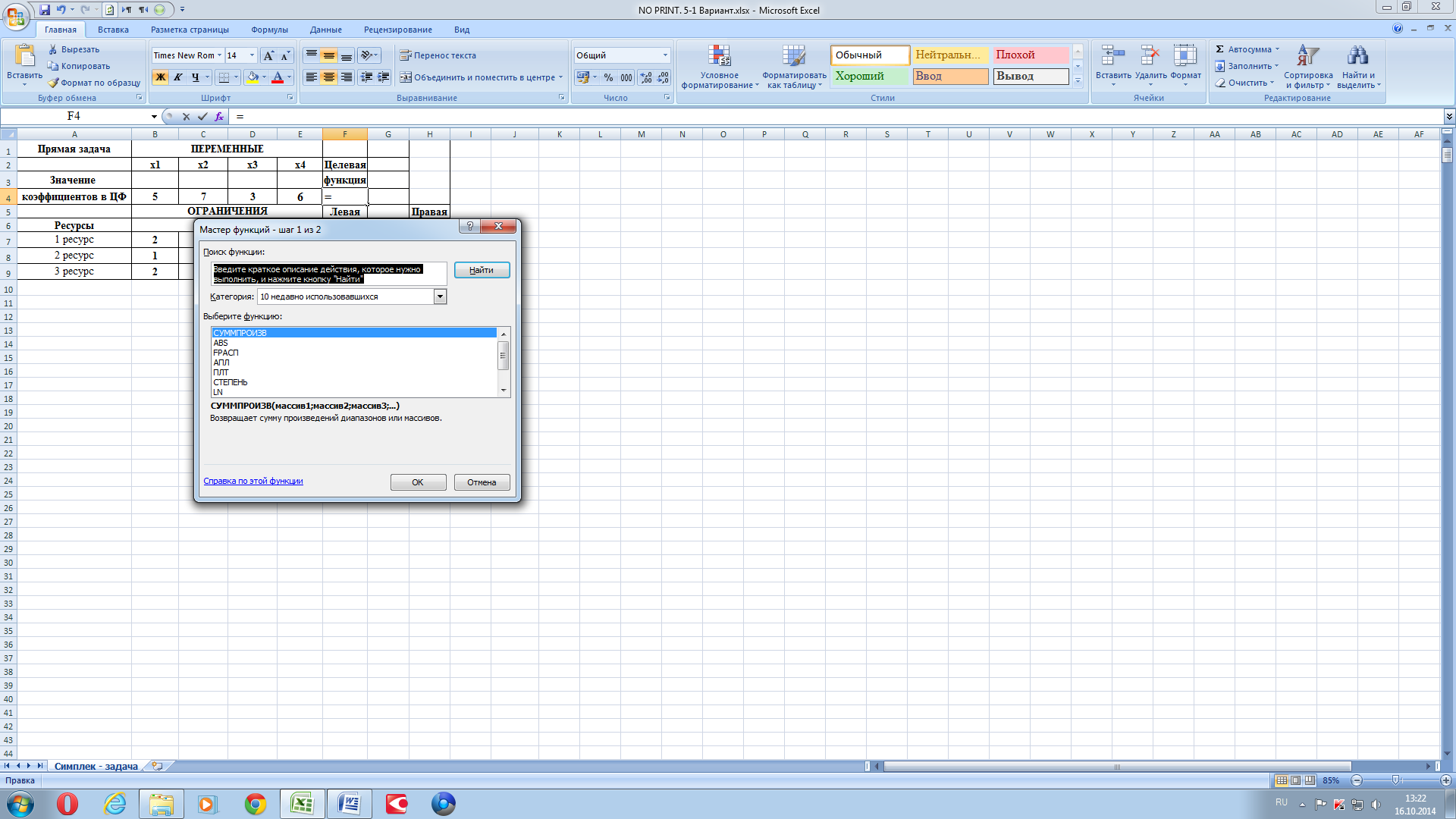
Рисунок 2.
Левой кнопкой мышки жьмём на строку «СУММПРОИЗВЕДЕНИЯ». Открывается окно.
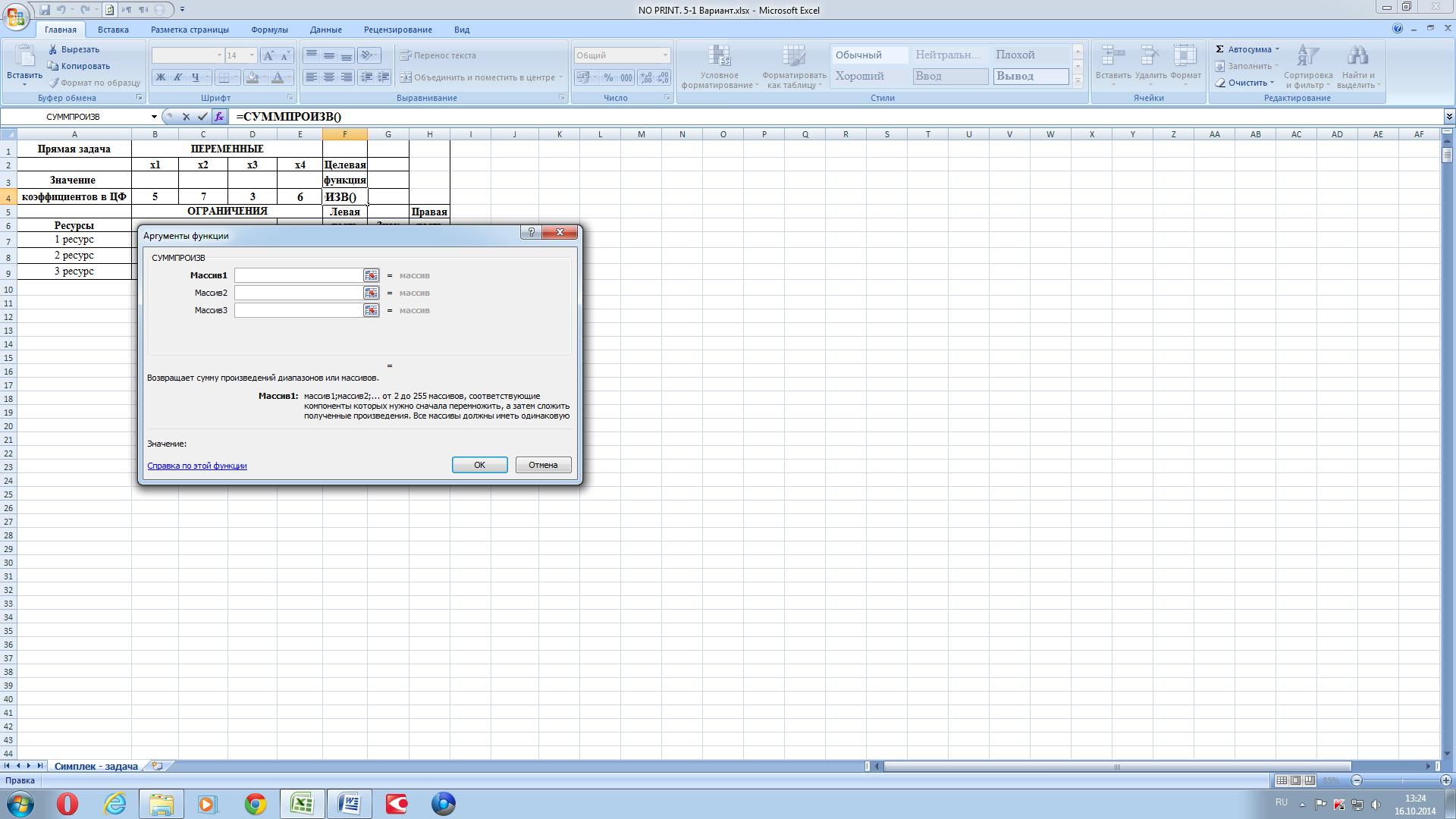
Рисунок 3.
В массив 1 ввести ячейки: «B$3» –«E$3».
В массив 2 ввести ячейки: «B4» –«E4». Жмём «Ok». Маркер помещаем в ячейку «F4». Далее, копируем содержимое ячейки «F4» в ячейку «F7». Маркер помещаем в ячейку «F4». Далее, копируем содержимое ячейки «F8» в ячейку «F7». Маркер помещаем в ячейку «F4». Далее, копируем содержимое ячейки «F4» в ячейку «F9».
Получаем рисунок 4.
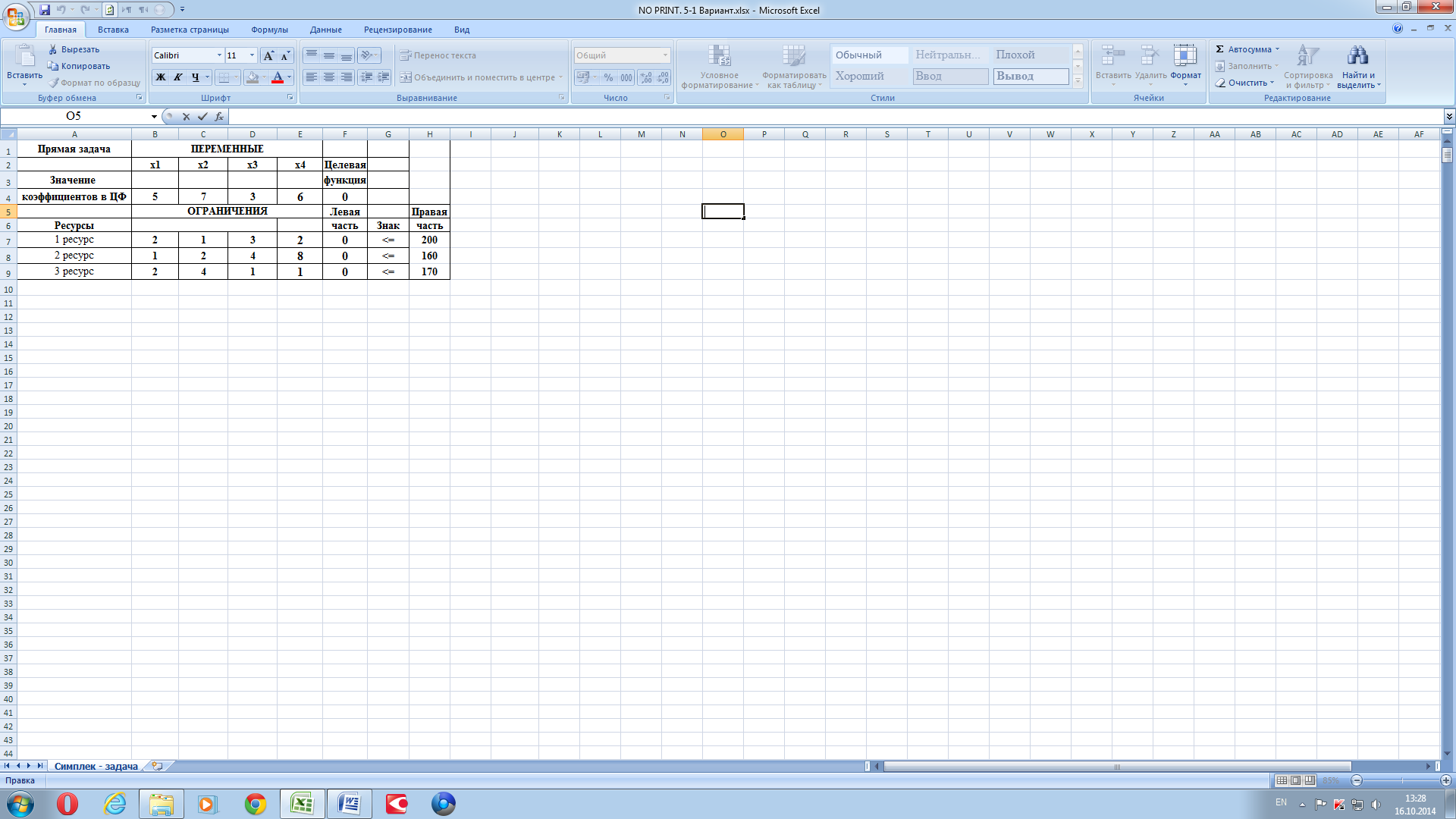
Рисунок 4.
Маркером ищем закладку «Данные».
После этой операции в «Закладках» появится закладка «Поиск решении».
Рисунок 5.
Нажимаем закладку «Поиск решения». Откроется окно (рисунок 6).
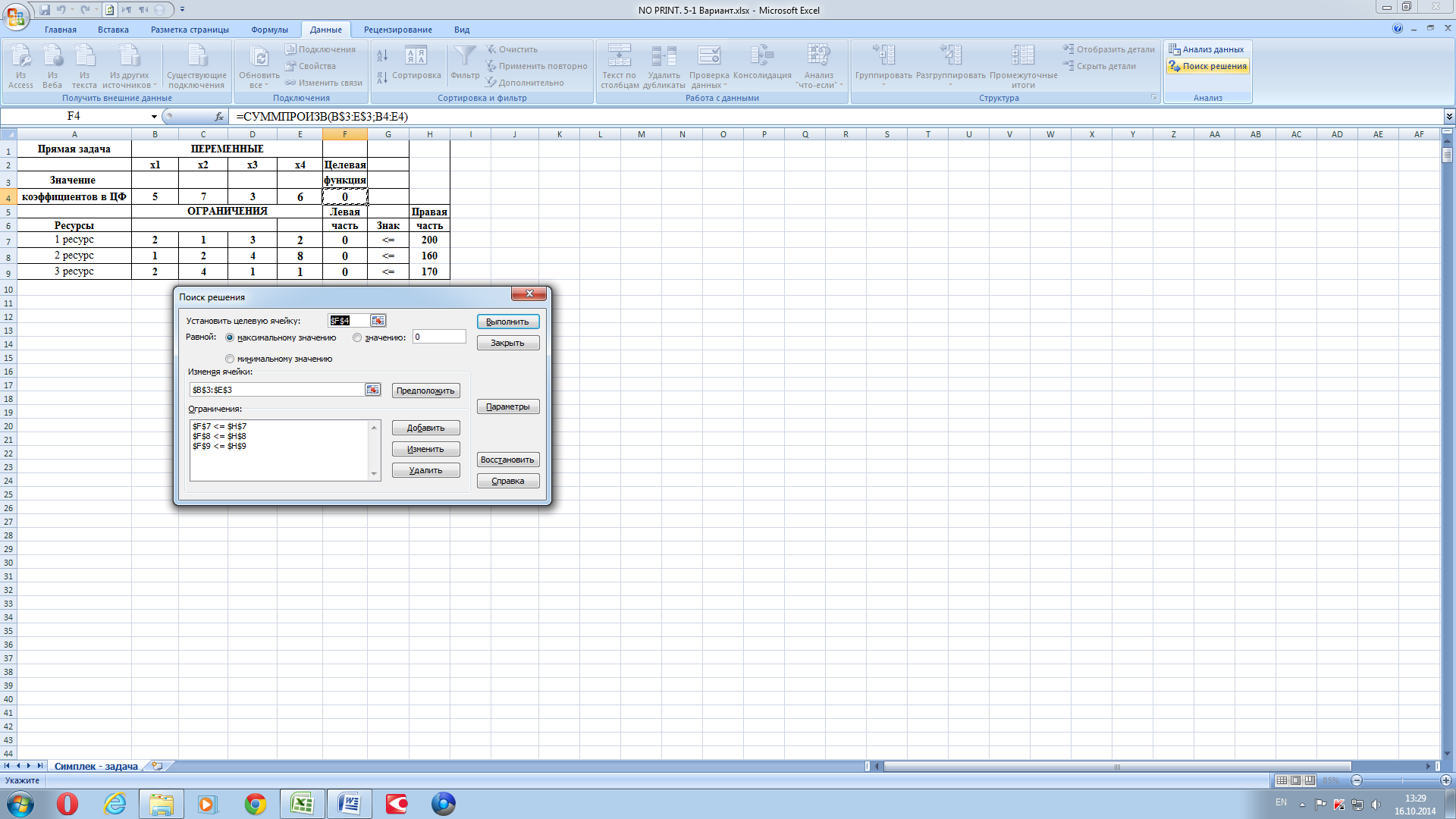
Рисунок 6.
Заполняем окно рисунка 6. Далее нажимаем «Параметры», получаем рисунок 7.
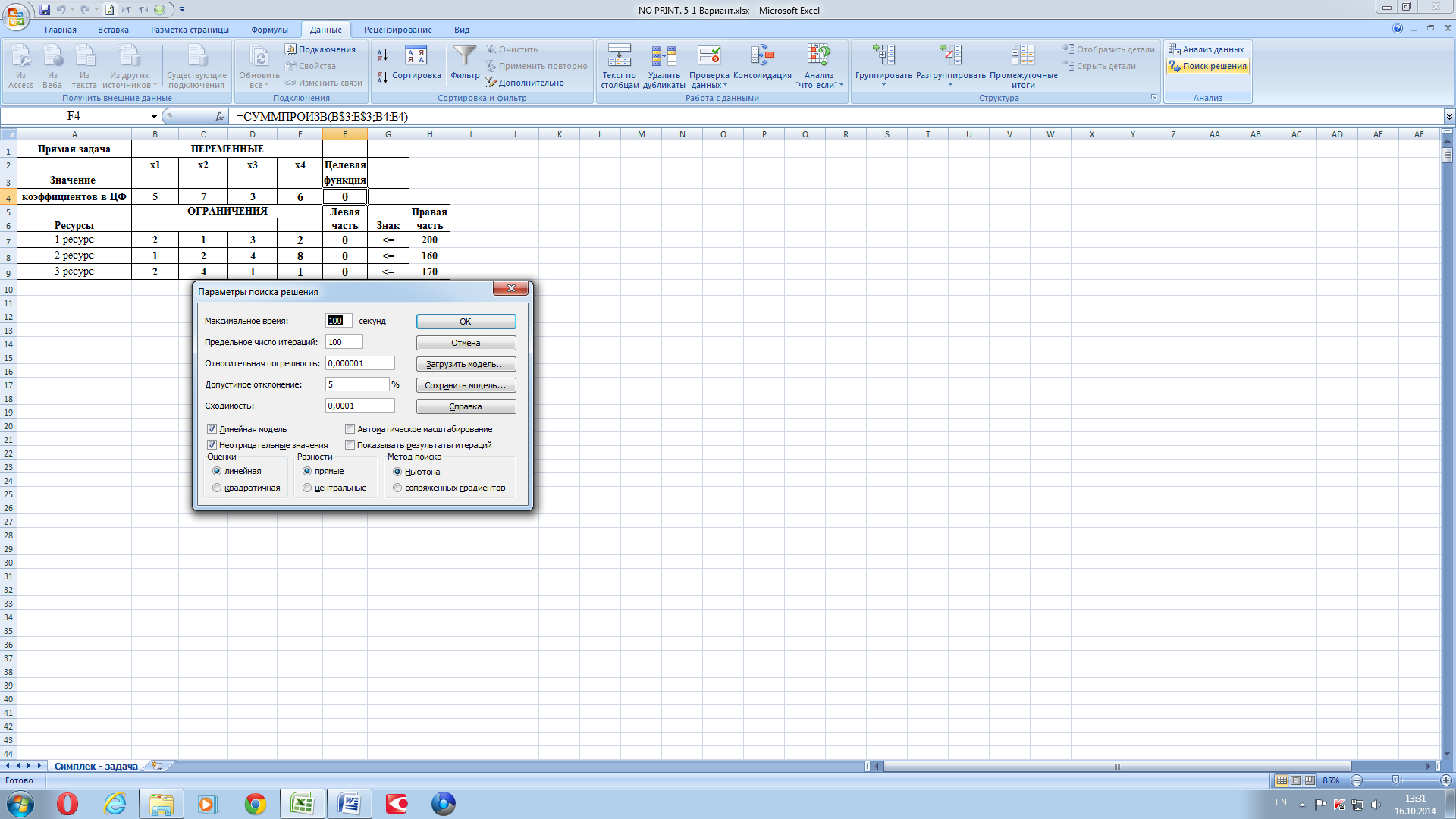
Рисунок 7.
Жмём «Ok». Получаем рисунок 8.
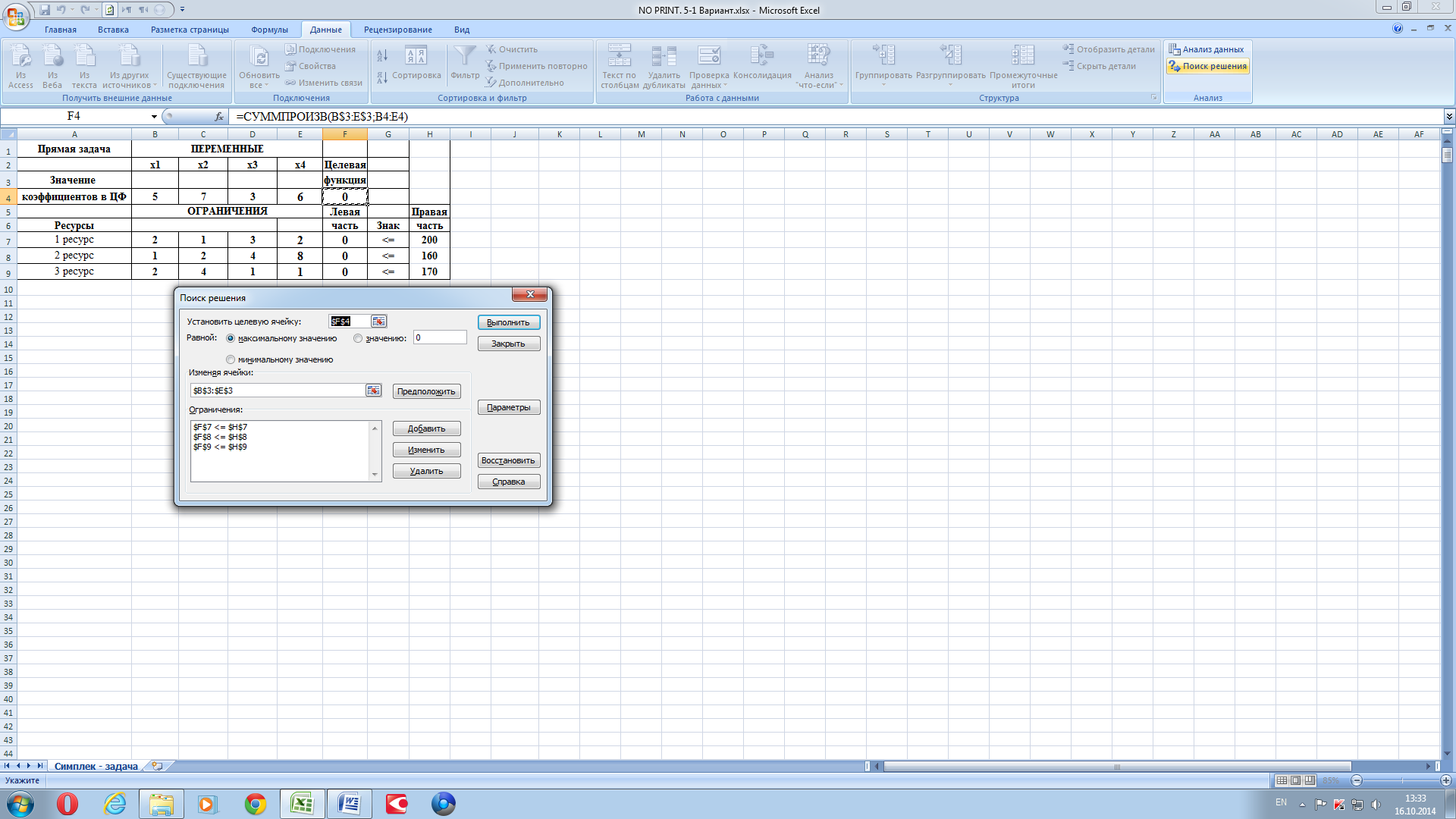
Рисунок 8.
Нажимаем «Выполнить». Получаем рисунок 9. Выделить типы «Отчётов».

Рисунок 9.
Жмём «Ok». Отчёты смотреть в файле Excel.
Задача решена.
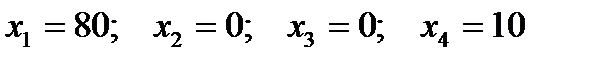 .
.
Максимум целевой функции равен:
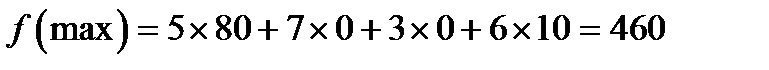 .
.
Из рисунка 9 видно, что ресурс 2 и 3 являются дефицитными ресурсами. Они используются полностью. Ресурс 1 используется не полностью. В остатке остаётся 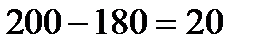 единиц первого ресурса.
единиц первого ресурса.
Никак не изменится общая прибыль при увеличении запасов сырья I вида на 8 единиц.
Ниже представим все отчёты: отчёт по результатам, отчёт по пределам, отчёт по устойчивости.
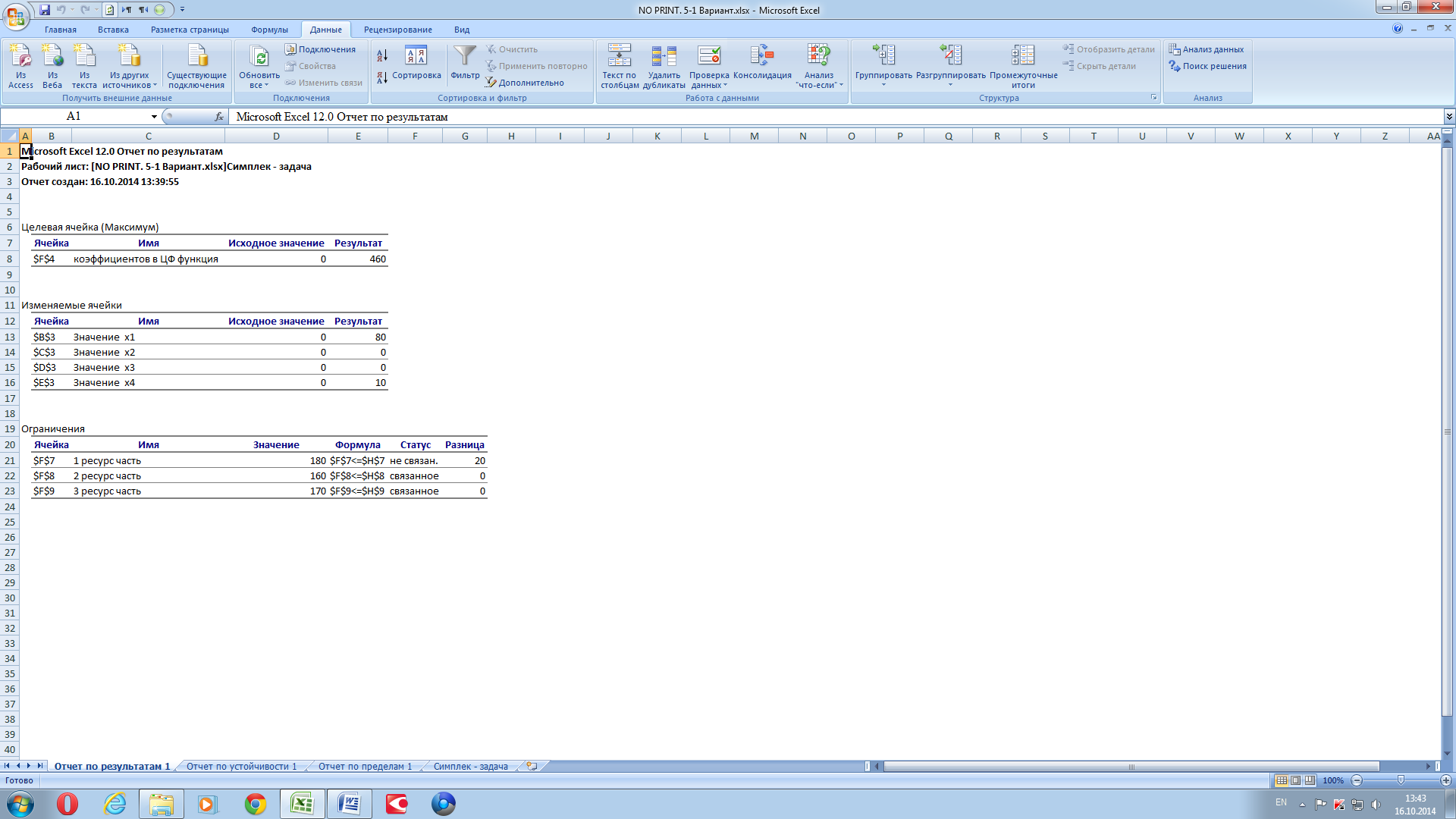
Рисунок 10. Отчёт по результатам.
Для ограничений в столбце Формула приведены зависимости, которые были введены в диалоговое окно ПОИСК РЕШЕНИЯ; в столбце Значение – величины использованного ресурса; в столбце Разница – количество неиспользованного ресурса. Если ресурс расходуется полностью, то в столбце Статус указывается «связанное»; при неполном использовании ресурса в этом столбце указывается «не связан». Для переменных показывается разность между значениями переменных в найденном оптимальном решении и заданным для них граничным условием.
В отчете по устойчивости (рис. 3.10) дан анализ по переменным и ограничениям. Исследование устойчивости оптимального решения – это изучение влияния изменений отдельно взятых параметров модели (оценок целевой функции, технико-экономических коэффициентов, объемов ограничений по ресурсам и продуктам, значений базисных переменных и др.) и ее структуры (введение новых ограничений и переменных или их сокращение) на показатели оптимального решения. Такой анализ позволяет судить о пределах допустимых изменений в оптимальном плане и о его устойчивости.
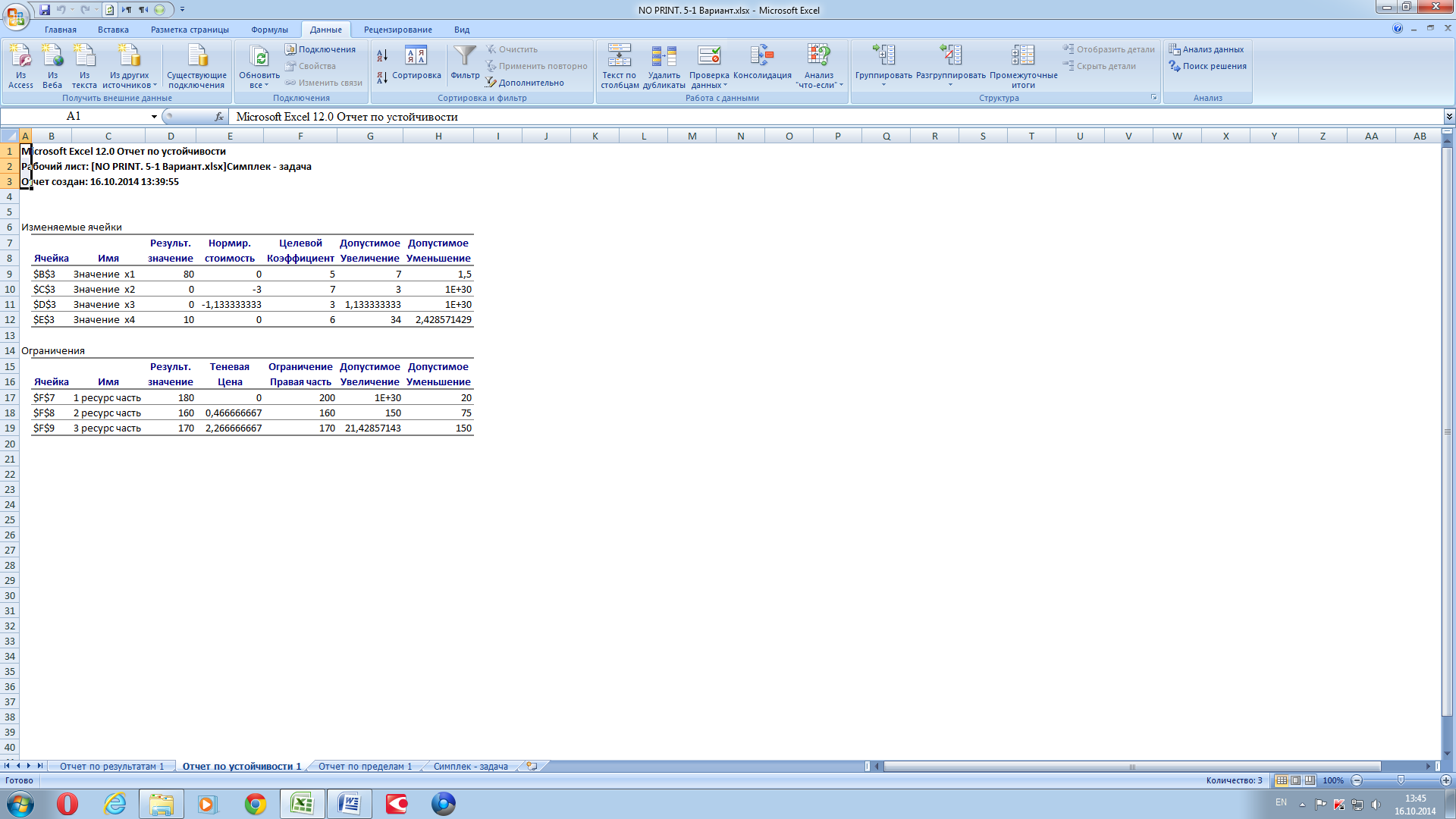
Рисунок 11. Отчёт по устойчивости.
В отчете по устойчивости (рис. 11) дан анализ по переменным и ограничениям. Исследование устойчивости оптимального решения – это изучение влияния изменений отдельно взятых параметров модели (оценок целевой функции, технико-экономических коэффициентов, объемов ограничений по ресурсам и продуктам, значений базисных переменных и др.) и ее структуры (введение новых ограничений и переменных или их сокращение) на показатели оптимального решения. Такой анализ позволяет судить о пределах допустимых изменений в оптимальном плане и о его устойчивости.
В результате решения в разделе Изменяемые ячейки приведены следующие данные:
· результирующие значения переменных;
· нормированная стоимость, т. е. дополнительные двойственные переменные, которые показывают, насколько изменяется значение целевой функции при принудительном включении единицы этой переменной в оптимальное решение;
· коэффициенты целевой функции;
· допустимые значения приращения коэффициентов целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение.
В разделе Ограничения приведены значения:
· величин используемых ресурсов;
· теневые цены, т. е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;
· значения приращения ресурсов, при которых сохраняется оптимальный набор двойственных переменных, входящих в оптимальное решение.
В отчете по пределам (рис. 3.11) показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.
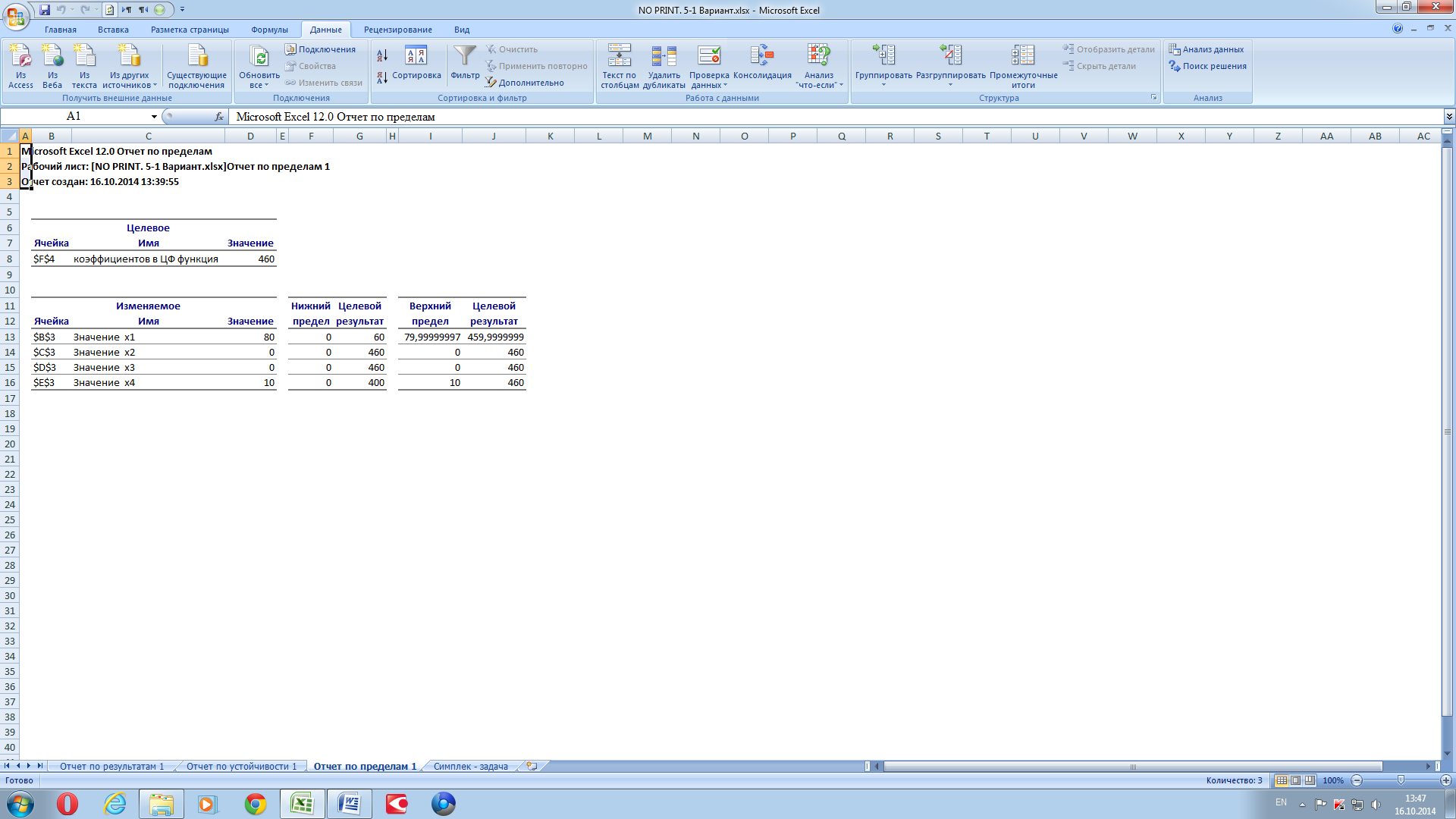
Рисунок 12. Отчёт по пределам.
Выводы
На основе Отчета по результатам можно сделать следующие выводы об оптимальном решении поставленной задачи:
· максимальное значение прибыли от продажи производимых товаров составляет 460 тыс. руб.;
· оптимальный план предусматривает производство товаров «А» и «Г» в количестве 80 и 10 шт. соответственно;
· ресурсы 2 и 3 типов расходуются полностью, и остается неиспользованным 20 ед. сырья 1 типа. Следовательно, ресурсы 2 и 3 типа являются дефицитными.
Согласно Отчету по устойчивости можно сделать следующие выводы:
· двойственные оценки (теневые цены) 2 и 3 типов ресурсов положительные. Это еще раз подтверждает, что ресурсы 2 и 3 типа являются дефицитными. Двойственная оценка 1 типа ресурсов показывает, что при его изменении на 8 единиц значение целевой функции не измениться. Следовательно, наиболее предпочтительным (с точки зрения увеличения запаса ресурсов) из дефицитных ресурсов является ресурс 3 типа, поскольку его изменение обеспечивает наибольший прирост целевой функции.
ДВОЙСТВЕННАЯ ЗАДАЧА.
Найдём двойственную задачу к прямой задаче (но не так подробно).
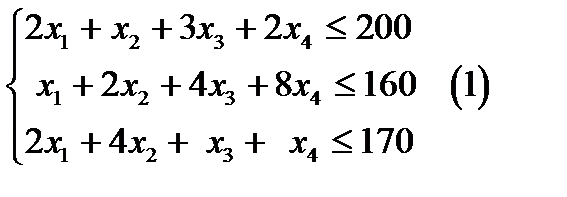 .
.
Целевая функция на максимум общей будет иметь вид:
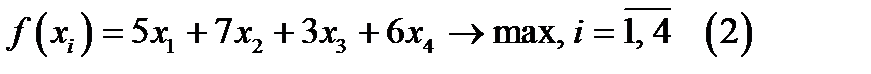 .
.
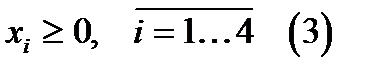 .
.
Запишем матрицу прямой задачи, в последней строке матрицы коэффициенты целевой прямой задачи.
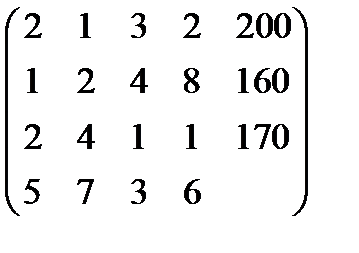 .
.
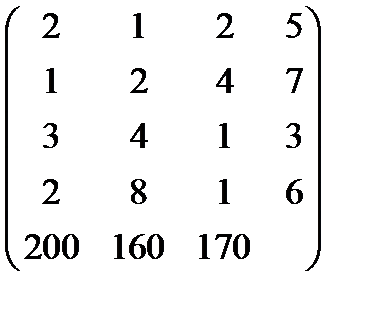
Транспонируем полученную матрицу.
 .
.
По транспонированной матрице составим двойственную задачу.
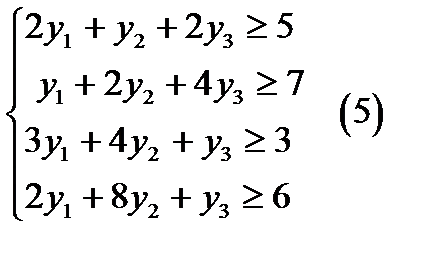 ,
,
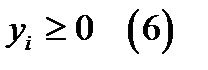 ,
,
Целевая функция двойственно задачи имеет вид:
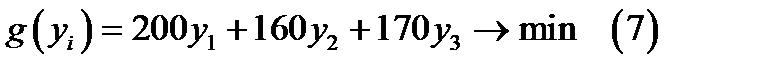 .
.
Записи (5), (6) и (7) представляют собой формальный вид двойственной задачи линейного программирования.
Решение двойственной задачи.
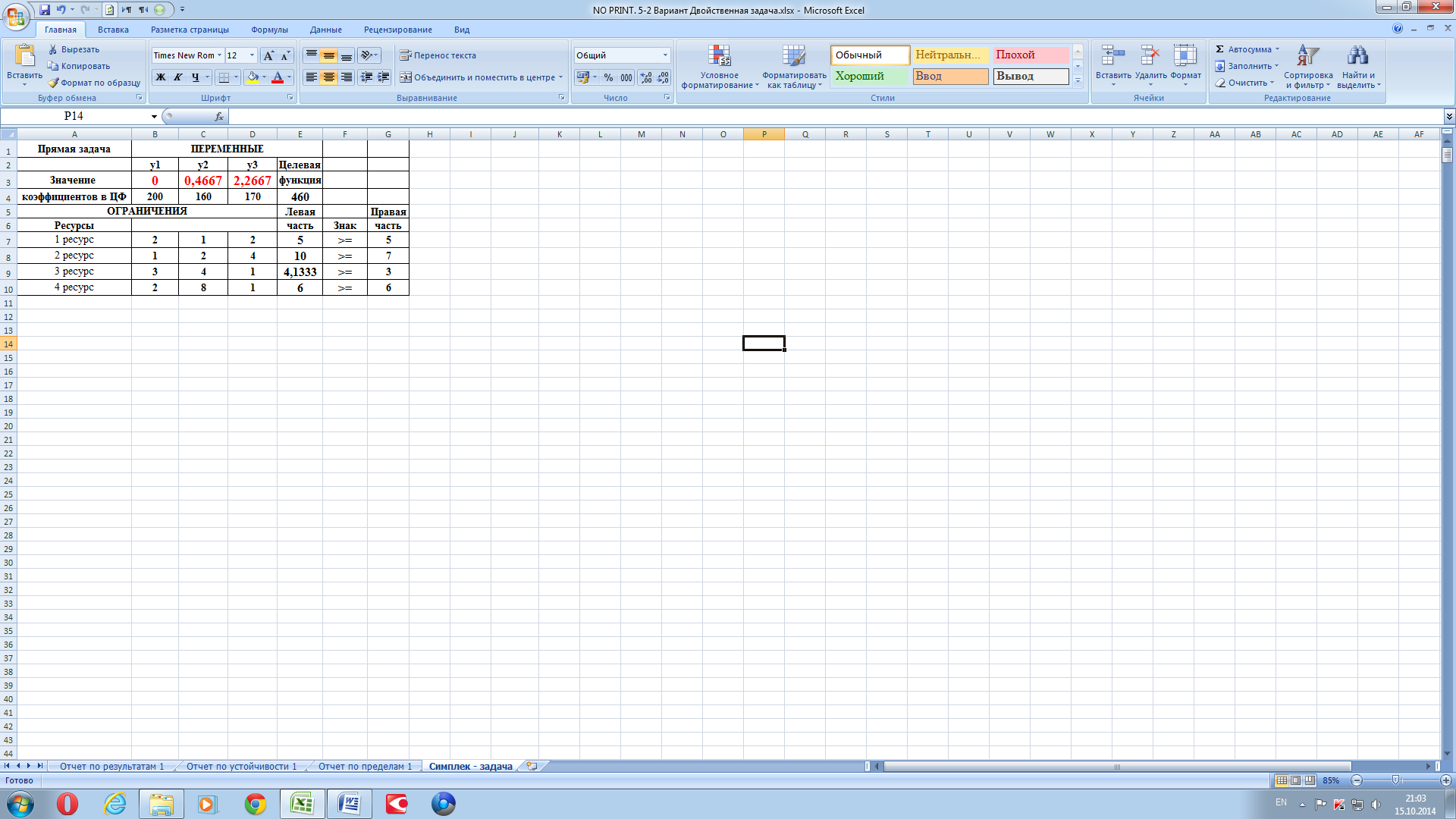
Рисунок 13.
Решение двойственной задачи.
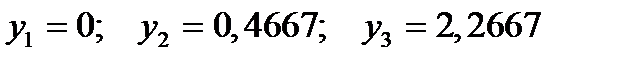 .
.
Минимум целевой функции для двойственной задачи равен:
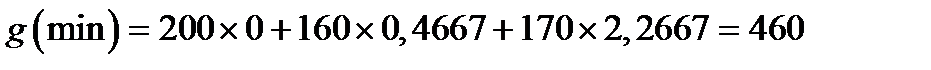 .
.
Как видим из решения 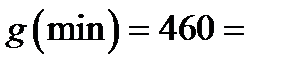
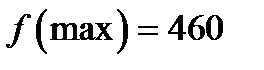 .
.
Представим отчёты двойственной задачи в Excel - файле.
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 3463; Нарушение авторских прав?; Мы поможем в написании вашей работы!