Логический тип

Турбо-Паскаль позволяет обрабатывать данные не только числового типа, но и других типов, например логического. Для обозначения логического типа используется ключевое слово boolean. Булевы (логические) переменные могут иметь одно из двух значений: true (истина) или false (ложь). Булевский тип является порядковым типом и упорядочен так, что false < true. По сравнению с типом real, который допускает миллионы различимых значений, может показаться, что тип boolean имеет ограниченную область применения. Однако, как это ни странно, именно ограниченность диапазона значений булевых переменных придает булевым выражениям их значимость.

Булевы выражения могут принимать несколько различных форм. Во-первых, они могут быть просто константами true (истина) или false (ложь). Оператор присваивания, использующий эту форму, аналогичен арифметическому оператору. Например, пусть переменные a и b логического типа:

var a,b:boolean;

тогда можно написать операторы:

a:=true;

b:=false.

Булевы выражения можно использовать для проверки отношений между двумя переменными: a>b,c<=d,k=m и т.д. Таким образом, условие в условном операторе является выражением логического типа. Кроме того, булевы выражения могут конструироваться с помощью булевых операций. Эти операции образуют инструментальный фундамент булевой логики, алгебры логики, разработанной в ХIХв. математиком Джорджем Булем. Рассмотрим три основные булевы операции.

Операция and – логическое пересечение (умножение, операция "и"). Выражение a and b дает значение true только в том случае, если a и b имеют значения true, в остальных случаях – false:

true and true = true

true and false = false

false and false = false

Операция or – логическое сложение (объединение, операция "или"). Выражение a or b дает значение false в том и только в том случае, если a и b имеют значения false, в остальных случаях – результат true:

true or true = true

true or false = true

false or false = false

Операция not – отрицание (операция "не"). Выражение not a имеет значение, противоположное значению a:

not true = false

not false = true

Эти операции полезны, если нужно проверить сложное условие:

if (a>b) and (a>c) then max:=a;

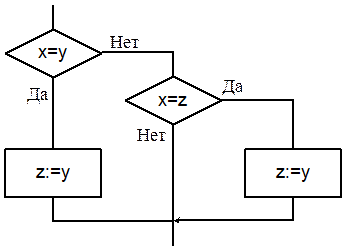
if (x=y) or (x=z) then z:=y;

Дата добавления: 2014-11-18