Метод простой итерации

2.

1.

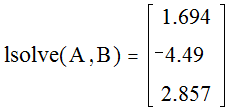
3. Метод Гаусса:

3.1. функция, переставляющая строки матрицы при обнаружении в текущей строке нулевого элемента на главной диагонали

3.2. прямой ход – приведение системы к треугольному виду

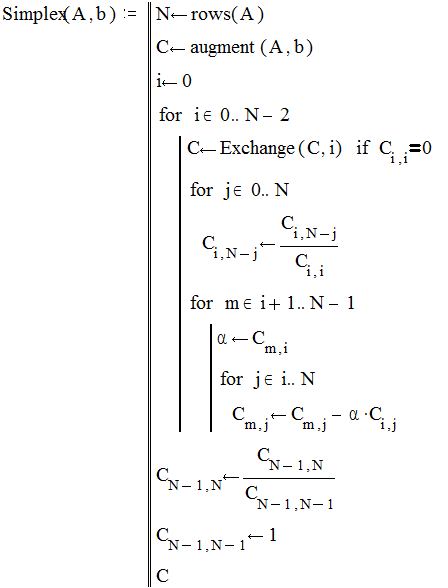
3.3. обратный ход – нахождение значений неизвестных:

3.4. Задайте матрицу системы и вектора-столбца свободных членов:

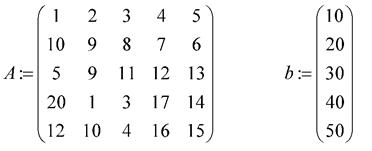
3.5. Проверьте правильность работы функции Simplex (прямой ход):

3.6. Решите систему линейных уравнений методом Гаусса (обратный ход):

3.7. Решите систему 2.1 методом Гаусса.

4.1. Решить систему линейных уравнений:

4.2. Приведите исходную систему к виду с преобладающими диагональными коэффициентами. Для этого, например, первое уравнение запишите третьим, третье уравнение умножьте на 2, вычтите второе и запишите на первом месте, а второе уравнение умножьте на 2, вычтите первое и запишите на втором месте

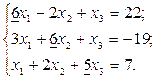
Коэффициенты, расположенные по диагонали и подчеркнутые, являются преобладающими по строке.

4.3. Составьте матрицы коэффициентов при неизвестных в левой части и свободных членов.

4.4. Получите преобразованную систему:

4.5. Получите систему:

Для обеспечения условий сходимости нужно получить такую систему, чтобы коэффициенты в правой части системы были существенно меньше еди­ницы.

4.6. Проверьте одно из условий сходимости итерационного процесса, для чего установите сходимость, т. е. "погрузите" систему в пространство с одной из трех метрик: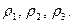

В пакете Mathcad коэффициенты сжатия можно определить с помощью функций normi (АА), norml (АА), norme (АА) (соответственно для: )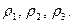

4.7. или воспользоваться формулами для определения коэффициента сжатия, данными ниже, набирая их учитывайте, что сначала набирается функция max(), а внутри скобок выберите матрицу 3 строки, 1 столбец и в каждой строке набирайте формулу, значок суммы берем из

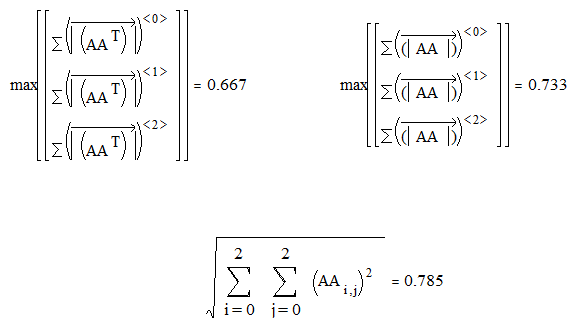
Заметьте, что все коэффициенты меньше единицы, значит, систему можно "погрузить" в пространство с любой из метрик. Остановимся на простран­стве с метрикой .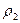

Итак, итерационный процесс сходится, причем 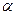= 0,733.

4.8. Найдите критерий достижения заданной точности при решении системы уравнений методом простой итерации. Для достижения точности 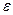= 0,001 приближения нужно находить до тех пор, пока будет выполняться нера­венство , т. е. расстояние между двумя сосед­ними приближениями не должно превышать числа Е.

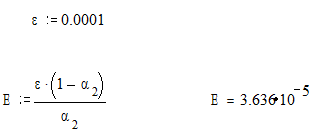
4.9. Вычислите значения итерационной последовательности:

4.10. Для определения, какое приближение будет являться решением, необходимо найти расстояния между двумя соседними приближениями по метрике 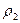(т. к. выбрано это пространство)

Введите формулу и поставьте равно:

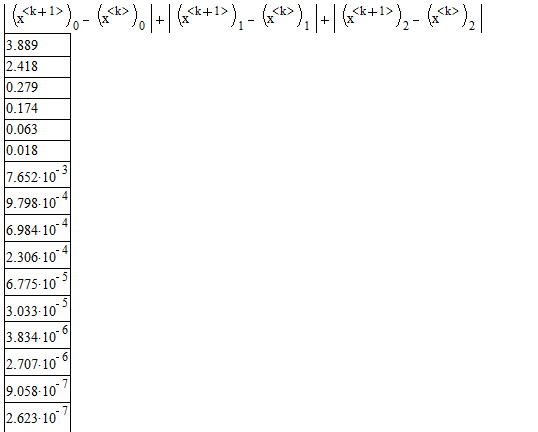
Полученное десятое значение суммы модулей разностей коэффициентов при неизвестных, равное , удовлетворяет условию критерия. Это значит, что в таблице значений х девятый столбец является решением системы уравнений методом простой итерации.

4.11. Визуализируйте полученные значения, построив график:

Графики показывают, что, начиная с к = 10, все три линии перестают преломляться, а значит, десятое приближение будет являться решением системы уравнений методом простой итерации.

Ответ: решением системы является вектор-столбец , полученный на десятом шаге итерации.

Дата добавления: 2014-11-18