Операції над висловленнями

Однією з основних задач логіки висловлень є дослідження операцій, за допомогою яких з певних вихідних висловлень утворюють нові висловлення. Такі операції і називають логічними.

Означення кожної логічної операції задаватимемо відповідною матрицею (таблицею), в перших стовпчи­ках якої записуються всі можливі істинісні значення компонентів, а в останньому стовпчику — істинісне значення результату операції.

Визначення 2 Бінарну логічну операцію, яка відповідає зв’язці “і” звичайної мови, позначається символом “Ù” і задається наступною матрицею, називають кон'юнкцією, або логічним множенням.

p	q	p Ù q

Вищенаведене табличне означення операції “кон'юнк­ція” рівнозначне такому словесному означенню: “Кон'юнкція p Ù q істинна тоді і тільки тоді, коли обидва компоненти р і q є одночасно істинними”.

У схемах управління логічна операція кон'юнкція реалізується в схемі збіги, показаної на рис. 1.2.

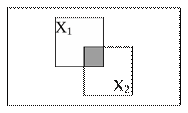
Рис. 1.2 –Діаграма Венна (кон'юнкція)

Визначення 3 Бінарну логічну операцію, відповідну зв’язці “або нероздільне”, що позначається символом “Ú” і задається наступною таб­лицею, називають диз’юнкцією або логічним додаванням.

p	q	p Ú q

Словесне означення диз'юнкції: “Диз’юнкція “ p Ú q ” істинна тоді і тільки тоді, коли принаймні один з її компонентів р або q є істинним, у протилежному випадку диз’юнкція є хибною”.

Операція диз'юнкції часто називається логічним складанням, а також логічною операцією "АБО" (рис. 1.3). Схему, відтворюючу операцію логічного додавання зазвичай називають збиральної схемою.

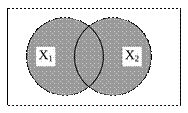
Рис. 1.3 – Діаграма Венна (диз'юнкція)

Зауважимо, що A Ú 1 = 1; A Ú Ā = 1.

З двох простих висловлювань за допомогою логічних зв'язків можна утворити 16 логічних висловлювань. Але заперечення, кон'юнкція і диз'юнкція є основними логічними зв'язками, так як всі інші можна утворити з основних логічних зв'язків.

Визначення 4 Унарну операція, відповідну виразу “неправильно, що”, яку позначають символом “—“ і задають наступною таблицею, називають логічнимзапереченням. Вираз „ 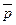” читають “не р ”.

p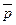

Словесне означення заперечення: “Заперечення ` 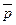істинне тоді і тільки тоді, коли р — хибне, у протилежному випадку` 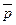— хибне” (рис. 1.4).

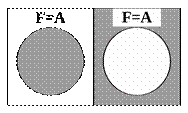
Рис. 1.4 – Діаграма Венна (заперечення)

Заперечення є найпростішою логічною операцією і єдиною логічною операцією, виконуваної над одним аргументом.

Зауважимо, що послідовне виконання двох операцій заперечення Ā призводить до вихідного значення А.

Визначення 5 Операцію, яка відповідає сполучнику “якщо..., то...”, позначається символом “®”, називають імплікацією. ЇЇ задають таблицею:

p	q	p ® q

В імплікації р називають антецеден­том або посиланням (умовою), q — консеквентом або висновком.

Словесне означення операції “імплікація” таке: “Імплікація „ p ® q ” хибна тоді і тільки тоді, коли її антецедент — істинний, а консеквент — хибний, в усіх інших випадках імплікація — істинна”.

Імплікацією висловлень А і В називається висловлювання, позначене символами А ® В, яке хибно тоді і тільки тоді, коли А істинно, а В хибно. Читається "А імплікує В". Імплікація - це логічна операція, відповідна союзу "якщо... то". Запис А ® У означає те ж, що і вислів: "якщо А то В", "з А випливає В" "А є достатня умова для В", для того щоб А необхідно, щоб В "," В є необхідна умова для А "," для того щоб В, достатньо щоб А ". Порівняємо такі пропозиції:

1. Якщо число n ділиться на 4, то воно ділиться на 2.

2. Якщо Іванов захоплений математикою, то Петров нічим не цікавиться.

Очевидно, що сенс союзу "якщо... то" в цих пропозиціях різний.

З визначення імплікації випливає, що:

1. Імплікація з помилковим антецедентом завжди істинна.

2. Імплікація з істинним консеквент завжди істинна.

3. Імплікація хибна тоді і тільки тоді, коли її антецендент істинний, а консеквент хибний.

Прийняте визначення імплікації відповідає вживанню союзу "якщо... то" в пропозиції "Якщо буде гарна погода, то я прийду до тебе в гості", яке ви розціните як брехня в тому випадку, коли погода гарна, а приятель до вас не прийде.

Разом з тим визначення імплікації змушує вважати істинним пропозиції як "Якщо 2х2 = 4, то Москва столиця Росії"; "Якщо 2х2 = 5, то я найкрасивіша дівчина Росії". Це пов'язано з тим, що визначеннями логічних операцій сенс складових висловлень не враховується, вони розглядаються як об'єкти, що володіють єдиною властивістю - бути істинними або помилковими (рис. 1.5).

Рис. 1.5 – Діаграма Венна (імплікація)

Визначення 6 Бінарну логічну операцію, яка відповідає зв’язці “тоді і тільки тоді”, позначається символом “«”, називають еквіваленцією. Її табличне означення:

p	q	p «q

Словесне означення еквіваленції можна сформулю­вати так: “Еквіваленція “ p «q ” істинна тоді і тільки тоді, коли p і q набувають однакових значень істинності, в протилежному випадку еквіваленція — хибна”.

Логічна операція еквівалентності, відповідає союзу "тоді і тільки тоді, коли" і читається "А еквівалентно В", "Для того, щоб А необхідно і достатньо, щоб В".

Коли ми говоримо "А тільки тоді, коли В" то маємо на увазі, що обидві пропозиції А і В одночасно істинні, або одночасно хибні. Наприклад, говорячи: "Я поїду в Ленінград тоді і тільки тоді, коли ти поїдеш до Києва", ми стверджуємо, що-небудь станеться і те і інше, або ні того, ні іншого. Можна довести використовуючи таблицю істинності, що для будь-яких висловлювань А і В висловлювання (А Û В) = 1 тоді і тільки тоді, коли (А Þ У) = 1 і (В Þ А) = 1.

Це твердження використовується при доказі теорем виду А Û В. Одним із способів доказу істинності висловлювання А Û В є доказ істинності висловлювання А Þ У (необхідність) і істинності висловлювання У Þ А (достатність).

Висловлювання А і В називаються рівносильними. Якщо (А Û В) = 1 кажуть, що формули F ₁ і F ₂ рівносильні, якщо їх еквіваленції F1 Û F2 - тавтологія (тотожне істинне висловлювання, що на рис. 1.6).

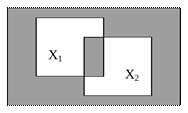
Рис. 1.6 – Діаграма Венна (еквіваленції)

Запис F ₁ º F ₂ читається: "формула F ₁ рівносильна формулою F _2"

А Û У º (А Þ В) Ù (В Þ А)

Рівносильність є відношення між формулами (також як рівність відношення між числами, паралельність - відношення між прямими). Ставлення равносильности володіє наступними властивостями:

а) рефлективності F º F

б) симетричності: якщо F ₁ º F ₂ то F ₂ º F ₁

в) транзитивності: якщо F ₁ º F ₂ і F ₂ º F _3, то F ₁ º F ₃

Висловлення, які не містять логічних зв'язок, нази­вають елементарними чи атомарними. Наприклад, висловлення “Рейк’явік — столиця Ісландії” і “3 — просте число” — елементарні висловлювання. Висловлення, яке містить хоча б одну логічну зв’язку,називають складним. Наприклад, висловлення “10 не є простим числом”.

Пропозиційні літери, символи логічних операцій та дужки – це вихідні символи алгебри висловлень.

Довільну послідовність вихідних символів називають виразом мови.

З множини виразів виділяють підмножину формул.

Формулами алгебри висловлень називають пропозиційні літери і вирази виду

`

F, F Ù G, F Ú G, F ® G, F «G,

де F, G – формули.

При цьому пропозиційні літери є елементарними (атомарними) формулами. Наприклад, (((p ®(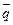))Ú r)Å s) – формула.

Дужки у формулі означають порядок виконання операції.

Символу кожної логічної операції відповідає пара дужок. Щоб запобігти громіздкості формул, використовують такі правила скорочення:

1) зовнішні дужки у записі кінцевої формули можна опустити;

2) всім логічним операціям приписують відповідний ранг, який знижується зліва на право: `, Ù, Ú, ®, «.

Порядок старшинства логічних операцій наступний: Ø, &, Ù, ®, «.

Лівіша операція є сильнішою за правішу.

Знаючи ранг операції можна не використовувати дужки.

1.4 Таблиці істинності

У таблиці істин­ності формули f (p, q, r) кожному символу логічної опера­ції в формулі f (p, q, r) відповідає окремий стовпчик таблиці, останній стовпчик відповідає істинісному значенню, яке визначається даною формулою (її головною операцією). Звернемо увагу на те, що кожен стовпчик таблиці істин­ності для формули f (p, q, r) відповідає певному кроку процесу її побудови або, як кажуть, певній підформулі f (p, q, r).

Наприклад, нехай задано функцію f (p, q, r)=(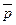 ® q Ú r)Ù(q ® p Ú` r).

p	q	r	`p	qÚr	`p ® q Ú r	` r	p Ú `r	q ® p Ú `r	f (p,q,r)

Часто таблицею істинності формули f (p ₁,..., p _n) називають скорочену таблицю, в якій з вищенаведеної залишають перших п стовпчиків (значень аргументів p ₁,..., p_n) і останній стовпчик.

Степінь складності таблиці істинності для формули f швидко зростає із збільшенням кількості різ­них пропозиційних букв, що входять до f. Так, при п = 3 кількість рядків таблиці дорівнює 2³ = 8, при п = 4 воно становить 2⁴= 16, при п = 5 дорівнює 2⁵= 32, а при п = 10 — вже 1024. Практично побудувати таблицю істин­ності в останньому випадку вже неможливо.

Означення 7 Формули алгебри висловлень f (p _1, ..., p_n), які на всіх наборах (p ₁, …, p_n), тобто при всіх можливих розподілах істинісних значень пропозиційних літер p ₁,..., p_n, набувають значення 1 (останній стовбець таблиці істинності - лише 1), називають тавтологіями, тотожно істинними формулами або законами алгебри висловлень.

Те, що формулаалгебри висловлень f є тавтологією, позначаютьтак: ⊨ f.

Означення 8 Формулу алгебри висловлень f (p ₁, ¼, p_n), яка набуває значення істинності 0 на всіх 2 ⁿ наборах, називають суперечністю. Найпростішим прикладом суперечності є формула p Ù .

Означення 9 Формулу алгебри висловлень, яка не є ні тавтологією, ні суперечністю, називають нейтральною. Прикладом нейтральної формули є p ® q.

Множини тавтологій, суперечностей і нейтральних формул попарно не перетинаються і разом становлять множину всіх формул алгебри висловлень.

Означення 10 Формулу алгебри висловлень, якане є суперечністю, називають виконуваною.

Так, формула р ® р — виконувана і формула р® теж виконувана при ½p½= 0; |p® |=1.

Означення 11 Висловлення називають логічно істинним (на базі алгебри висловлень) тоді і тільки тоді, коли його логічна структура є тавтологією.

Прикладом логічно істинного твердження є “Трикутник АВС — рівнобедрений або трикутник АВС — не рівнобедрений” (логічна структура цього твердження — р Ú ).

Означення 12 Формули алгебри висловлень f (p ₁, ¼, p_n) і g (p ₁, ¼, p_n) називають рівносильними або логіч­но еквівалентними, якщо їх функції істин­ності | f | і | g | тотожно рівні, тобто, якщо їх значення на всіх 2 ⁿ наборах збігаються.

Рівносильність формул f і g позначатимемо f º g Символ “º” не є символом операції алгебри висловлень, а означає певне відношення між формулами.

Основні рівносильності (закони) алгебри висловлень:

1. p Ù q º q Ù p – комутативність кон’юнкції.

2. p Ú q º q Ú p – комутативність диз’юнкції.

3. p Ù(q Ù r)º(p Ù q)Ù r – асоціативність кон’юнкції.

4. p Ú(q Ú r)º(p Ú q)Ú r – асоціативність диз’юнкції.

5. p Ù(q Ú r)º p Ù q Ú p Ù r – перший дистрибутивний закон.

6. p Ú(q Ù r)º(p Ú q)Ù(p Ú r) – другий дистрибутивний закон.

7. 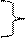(p Ù q)º Ú 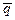закони

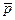8. (p Ú q)º Ù 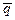де Моргана.

9. p ® q º Ú q.

10. p «q º(p ® q)Ù(q ® p).

11. º p – закон подвійного заперечення.

12. 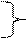p Ù p º p. закони

13. p Ú p º p. ідемподентності.

14. p ® q º ® .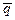

15. 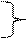p Ú p Ù q º p. закони

16. p Ù(p Ú q)º p. поглинання.

17. uÙ1ºu. правила

18. uÙ0º0. співвідно-

19. uÚ1º1. шення

20. uÚ0ºu. констант

21. p Ú 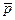º1 – закон виключення третього.

22. p Ù 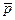º0 – закон протиріччя.

1.5 Алгоритм побудови формули за таблицею істинності

1. Виділити ті рядки таблиці істинності, в останніх стовпчиках яких міститься величина функції 1.

2. Виписати для кожного такого виділеного рядка кон'юнкцію (логічне «і») таким чином: якщо величина змінної цьому рядку дорівнює 1, то в кон'юнкцію записати позначення цієї змінної, інакше — її заперечення.

3. Всі отримані на попередньому кроці кон'юнкції записати елементами диз'юнкції (логічного «або»).

Приклад скорочення логічних виразів (спрощення логічних формул):

.

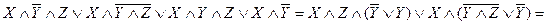
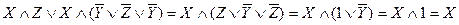Дата добавления: 2014-11-08