
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Угловая скорость
|
|
|
|
Кинематика вращательного движения
Наиболее простой случай вращательного движения абсолютно твердого тела – вращение относительно неподвижной оси – движение, при котором точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения.
При описании вращательного движения удобно пользоваться полярными координатами R и φ, где R – расстояние от полюса (центра вращения) до материальной точки, а φ – угол поворота (полярный угол).
 |
Угловое перемещение
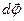 - векторная величина, модуль которой равен углу поворота, а направление совпадает с направлением поступательного движения правого винта (рис.1.6).
- векторная величина, модуль которой равен углу поворота, а направление совпадает с направлением поступательного движения правого винта (рис.1.6).
Для измерения угла поворота φ в системе СИ используют единицу измерения – радиан.
Угловой скоростью тела называют вектор  , численно равный первой производной угла j по времени, направленный вдоль оси вращения по правилу буравчика, так же как вектор
, численно равный первой производной угла j по времени, направленный вдоль оси вращения по правилу буравчика, так же как вектор 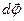 :
:
 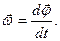
| (1.2.1.) |
Угловая скорость  (единица измерения в СИ -
(единица измерения в СИ -  ) характеризует направление и быстроту вращения тела вокруг оси. Если
) характеризует направление и быстроту вращения тела вокруг оси. Если 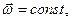 то движение называют равномерным вращением вокруг неподвижной оси.
то движение называют равномерным вращением вокруг неподвижной оси.
Скорость  произвольной точки M тела, вращающегося с угловой скоростью
произвольной точки M тела, вращающегося с угловой скоростью  , часто называют линейной скоростью этой точки.
, часто называют линейной скоростью этой точки.
линейная скорость υ точки связана с угловой скоростью ω и радиусом R траектории соотношением
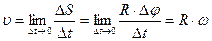 ,
,
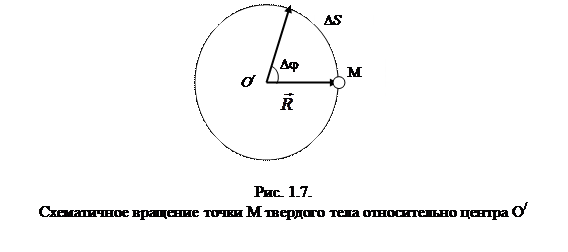 |
где DS – путь, который проходит точка за время Dt (рис.1.7.).
В векторном виде формулу для линейной скорости можно записать как векторное произведение
 . .
| (1.2.2,а) |
Модуль линейной скорости
 . (1.2.2,б)
. (1.2.2,б)
При равномерном вращении угловая скорость 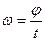 , а угол поворота
, а угол поворота  .
.
Единицей угловой скорости в системе СИ является радиан в секунду 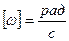 .
.
Угловая скорость w - есть величина постоянная, она указывает, на какой угол поворачивается тело за единицу времени. В этом случае она называется круговой или циклической частотой.
Равномерное движение можно охарактеризовать также периодом обращения. Периодом вращения T называют промежуток времени, в течении которого тело равномерно вращаясь с угловой скоростью w, совершает один оборот, то есть j = 2p:

Частотой вращения n называют число оборотов, совершаемых телом за 1 секунду при равномерном вращении:
 , , 
| (1.2.3) |
Единица частоты вращения – герц (Гц).
Угловое ускорение
Быстрота изменения угловой скорости характеризуется угловым ускорением  (в СИ единицей углового ускорения является
(в СИ единицей углового ускорения является  ):
):

| (1.2.4,а) |
 |
При неподвижной оси вращения векторы
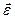 и
и  коллинеарны и направлены вдоль оси вращения. При ускоренном вращении
коллинеарны и направлены вдоль оси вращения. При ускоренном вращении  векторы
векторы 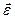 и
и  одинаково направлены, при замедленном вращении
одинаково направлены, при замедленном вращении  - противоположно направлены.
- противоположно направлены.
Направим ось OZ по оси вращения OO/(см. рис. 1.8), при этом проекция вектора  на ось OZ:
на ось OZ:
 . .
| (1.2.4,б) |
Ускорение  произвольной точки M тела, вращающегося с угловым ускорением
произвольной точки M тела, вращающегося с угловым ускорением  , называют линейным ускорением этой точки. Согласно выражению (1.1.12) линейное ускорение представляет собой векторную сумму тангенциального и нормального ускорений точки M твердого тела, причем,
, называют линейным ускорением этой точки. Согласно выражению (1.1.12) линейное ускорение представляет собой векторную сумму тангенциального и нормального ускорений точки M твердого тела, причем,  а
а 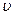 =w×R (см. (1.2.2,а)) и, как следствие,
=w×R (см. (1.2.2,а)) и, как следствие, 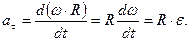 Что касается нормального ускорения
Что касается нормального ускорения 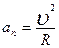 , то с учетом уравнения (1.2.2,а) можно получить:
, то с учетом уравнения (1.2.2,а) можно получить:  Таким образом, модуль линейного ускорения равен
Таким образом, модуль линейного ускорения равен

| (1.2.5) |
Из рис. 1.8 следует, что вектор тангенциального ускорения  , сонаправленный с вектором линейной скорости
, сонаправленный с вектором линейной скорости 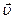 , перпендикулярен как вектору
, перпендикулярен как вектору  , так и вектору
, так и вектору 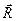 , и направлен в ту же сторону, что и результат векторного произведения
, и направлен в ту же сторону, что и результат векторного произведения  Таким образом,
Таким образом,
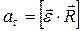
| (1.2.6,а) |
С учетом того, что  (см. рис. 1.8), можно показать:
(см. рис. 1.8), можно показать:
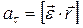
| (1.2.6,б) |
Нормальное ускорение направлено противоположно радиусу - вектору 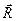 проведенному в точку M из центра окружности (по которой движется точка M) (см. рис. 1.8). Поэтому
проведенному в точку M из центра окружности (по которой движется точка M) (см. рис. 1.8). Поэтому

| (1.2.6,в) |
где 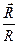 - единичный вектор, направленный по радиусу - вектору
- единичный вектор, направленный по радиусу - вектору 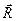
уравнения кинематики вращательного движения твердого тела относительно оси OZ OO/
1. Равномерное вращение.
 , wz = w = const > 0. При этом (см. (1.2.1))
, wz = w = const > 0. При этом (см. (1.2.1))

| (1.2.7) |
где j0 – значение j в начальный момент времени (t = 0).
2. Равнопеременное вращение относительно оси OZ.
e z = const. При ez > 0 – вращение равноускоренное; При e z < 0 – вращение равнозамедленное; wz = w = const > 0. Из выражения (1.2.4,б) следует, что
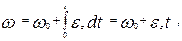
| (1.2.8) |
где w0 – начальная скорость. Кроме того,
 . .
| (1.2.9) |
Часто для простоты записи в выражениях (1.2.8) и (1.2.9) вместо e z используют e.
Путь, который проходит твердое тело при равноускоренном вращательном движении
 .
.
В целом полученные выше сведения по кинематике можно занести в таблицу аналогий (табл. 1).
Таблица 1
| Поступательное движение | Вращательное движение | Формулы связи |
 S S
| 
| S = R×j |

| 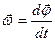
| 
|


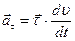

| 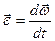
| 
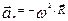
|
| Равномерное движение | ||
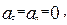 
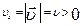

| 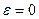 ,
wz = w = const > 0 ,
wz = w = const > 0

| |
| Равнопеременное движение | ||
 a n = 0, a t = const a n = 0, a t = const 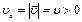
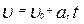

|  ez = const;
wz = w = const > 0 ez = const;
wz = w = const > 0

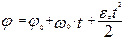
|
Глава 2. Динамика
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 1244; Нарушение авторских прав?; Мы поможем в написании вашей работы!