Первое начало термодинамики

Работа в термодинамике.

Первое начало термодинамики выражает закон сохранения энергии для тех макроскопических явлений, в которых одним из существенных параметров, определяющих состояние тел, является температура. Существует две формулировки первого начала термодинамики.

1) Приращение внутренней энергии системы всегда равно сумме совершаемой над системой работы А' и количества сообщенной системе теплоты Q:

DU = Q + А'

(8.2.1,а)

2) Обычно вместо работы А', совершаемой внешними телами над системой, рассматривают работу А, равную (-А'), совершаемую системой над внешними телами. Подставив (-А) вместо А' и выразив Q в уравнении (1), получаем:

Q=DU + А

(8.2.1,б)

Уравнение (8.2.1,б) выражает первое начало термодинамики: теплота, сообщенная системе в процессе изменения ее состояния, расходуется на изменение ее внутренней энергии и на совершение работы против внешних сил.

Внутренняя энергия может и увеличиваться и уменьшаться при передаче теплоты системе. Если энергия убывает (DU=U₂–U₁<0), то согласно (8.2.1,б) А>Q, т.е. система совершает работу как за счет получаемой теплоты Q, так и за счет запаса внутренней энергии, убыль которой равна (DU =U₁–U₂).

Часто приходится разбивать рассматриваемый процесс на ряд элементарных процессов, каждый из которых соответствует весьма малому изменению параметров системы. Запишем уравнение (8.2.1,б) для элементарного процесса в дифференциальном виде:

δQ=dU+δA,

(8.2.2)

где dU – малое изменение внутренней энергии; δ Q – элементарное количество теплоты; δ А – элементарная работа.

Между dU, δQ и δ А есть принципиальное отличие. Внутренняя энергия является функцией состояния тела. Поэтому ее изменение зависит только от начального и конечного состояний тела. Работа и количество теплоты зависят не только от этих состояний, но и от способа проведения процесса. Они не являются функциями состояния, а являются функциями теплового процесса. По отношению к работе и теплоте не может быть поставлен вопрос: какова теплота системы в данном состоянии. Следовательно, теплота характеризует процесс передачи внутренней энергии от одной системы к другой в форме тепла, то есть теплота характеризует не запас, а процесс. Поэтому в уравнении первого начала термодинамики dU представляет собой полный дифференциал, a δQ и δ A не являются полными дифференциалами, а представляют собой лишь малые величины.

Из уравнений (8.2.1,б) и (8.2.2) видно, что если процесс круговой, т.е. в результате него система возвращается в исходное состояние, то DU = 0 и, следовательно, Q=А. В круговом процессе все тепло, полученное системой, идет на производство внешней работы.

Если U₁=U₂ и Q=0, то А=О. Это значит, что невозможен процесс, единственным результатом которого является, производство работы без каких бы то ни было изменений в других телах, т.е. невозможен перпетуум мобиле – вечный двигатель первого рода.

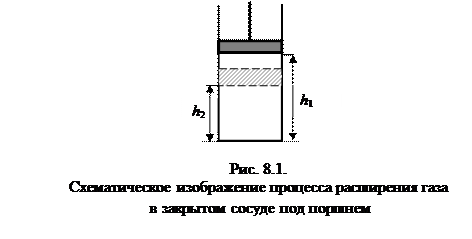Рассмотрим процесс расширения газа. Пусть в цилиндрическом сосуде заключен газ, закрытый подвижным поршнем (рис.8.1).

Предположим, что газ расширяется. Он будет перемещать поршень, и совершать над ним работу. При малом смещении dh=h₂-h₁ газ совершит работу

δA = F·dh,

где F –сила, с которой газ действует на поршень.

Учитывая, что

F=p·S

получим что, элементарная работа

δA= p·S·dh = p·dV, (8.2.3)

где dV= S·dh – малое изменение объема газа, р – давление газа в начале пути dh.

Работа, совершаемая при конечных изменениях объема, должна вычисляться путем интегрирования. Полная работа расширения:

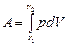(8.2.4)

На графике зависимости давления газа от объема (рис.8.2.) работа равна площади фигуры, ограниченной двумя ординатами и функцией p(V).

Предположим, система переходит из одного состояния в другое, совершая работу по расширению, но двумя различными путями I и II: p₁(V) и p₂(V).

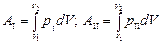
Работа A_I численно равна площади фигуры, ограниченной кривой I, А_II – площади фигуры, ограниченной кривой II: A_I № А_II. Работа различна, следовательно, работа не является функцией состояния.

Дата добавления: 2014-11-18