Методы наблюдения интерференции света. Расчет интерференционной картины от двух источников

Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников S₁ и S₂, имеющих вид параллельных, тонких светящихся нитей либо узких щелей (рис.18.1.).

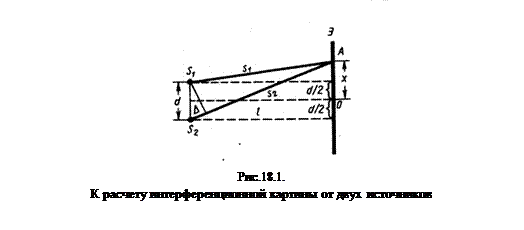Если в области, в которой волны перекрываются, внести экран, то на нем будет видна интерференционная картина, которая имеет вид чередующихся светлых и темных полос. Рассчитаем положение полос и их ширину. Экран поместим параллельно обеим щелям на одинаковом расстоянии l. Начало отсчета выберем в точке O, относительно которой S₁ и S₂ расположены симметрично. Источники будем считать испускающими свет в одинаковой фазе. Из рисунка видно, что

, .

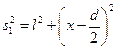Следовательно

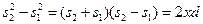
и оптическая разность хода равна

.

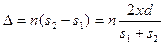Разность хода S ₂ – S ₁ составляет несколько длин волн и всегда значительно меньше S₁ и S₂ (S₁≈S₂=S). Поэтому можно положить S₁+S₂≈2S и

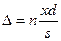. (18.2.1)

В большинстве случаев l>>х, поэтому S ≈ l, т.е.

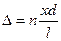(18.2.2)

Подстановка значения D в условие (18.1.4) дает, что максимумы интенсивности будут наблюдаться при значениях

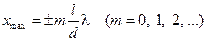. (18.2.3)

где 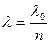- длина волны в среде.

Подставив (18.2.3) в условие (18.1.5), получим координаты минимумов интенсивности

. (18.2.4)

Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между соседними минимумами - шириной интерференционной полосы. Из (18.2.3) и (18.2.4) следует, что эти расстояния имеют одинаковое значение

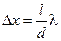. (18.2.5)

1. Метод Юнга. Источником света служит ярко освещенная щель S (рис18.2.), от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂ , параллельные щели S.

Таким образом, щели играют роль когерентных источников. Интерференционная картина наблюдается на экране (Э), расположенном на некотором расстоянии от щелей S₁ и S₂. В такой постановке Юнг осуществил первое наблюдение интерференции.

2. Зеркала Френеля. Два плоских зеркала (рис.18.3.), расположены относительно друг друга под небольшим углом.

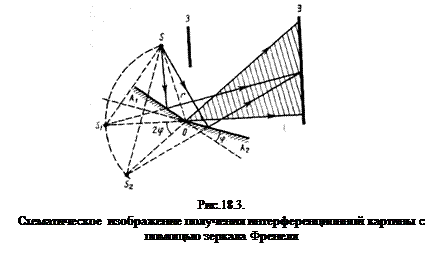На расстоянии r от линии пересечения зеркал параллельно ей находится прямолинейный источник света S. Световые пучки, отразившись от зеркал, являются мнимыми изображениями S в зеркалах. Мнимые источники S₁ и S₂ взаимно когерентны, и их световые пучки интерферируют в области взаимного перекрытия. От прямого попадания света на экран предохраняет заслонка.

Бипризма Френеля. Она состоит из двух одинаковых с общей гранью призм с малыми преломляющими углами (рис.18.4.).

Свет от прямолинейного источника S преломляется в обеих призмах, в результате чего образуются две когерентные цилиндрические волны, исходящих из мнимых источников 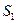и 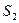. На поверхности экрана в некоторой его части происходит наложение этих волн и наблюдается интерференция.

Дата добавления: 2014-11-18