Пример решения задачи 1

Стальной ступенчатый стержень (рис.1.1.1) находится под действием продольной силы F и собственного веса (γ = 78 кН/м³). Требуется:

1) построить эпюры продольных усилий и напряжений;

2) определить опасное сечение и произвести проверочный расчет стержня, если σ_adm = 160 МПа;

3) определить удлинение стержня (Е = 2·10⁵ МПа).

Исходные данные:

А= 10 см²;

F = 10 кН;

l₁ = 1 м;

l₂ = 1.4 м;

l₃ = 1.6 м.

Рис. 1.1.1.

РЕШЕНИЕ:

1. При учете собственного веса стержня расчетная схема задачи имеет вид представленный на рис.1.1.2, где n₁ = g×A = 0,078 кН/м,

n₂ = g×2A = 0,156 кН/м, n₃ = g×2,4 A = 0,187 кН/м.

Для определения внутренних усилий применяется метод сечений. Стержень разбивается на участки. Границами участков служат сечения, в которых приложены внешние силы, изменяются площадь поперечного сечения или характер нагружения. На каждом участке стержень мысленно рассекается плоскостью перпендикулярной к оси стержня. Положение выбранного сечения фиксируется координатой X. Отбрасывается одна из отсеченных частей и действие отброшенной части заменяется внутренними усилиями, которые определяются из условия равновесия отсеченной части.

Эпюрой внутренней силы называется график, показывающий распределение этой силы вдоль оси стержня.

При центральном растяжении (сжатии) в поперечных сечениях стержня возникает только один внутренний силовой фактор – продольная сила N. Нормальные напряжения в поперечном сечении стержня определяются по формуле . Продольная сила N и нормальное напряжение s считаются положительными, если они вызывают растяжение продольных волокон стержня.

В данном случае стержень разбивается на три участка, площади поперечных сечений которых

А₁ = А= 10 см²; А₂ = 2×А = 20 см²; А₃ = 2,4×А = 24 см².

I участок: (0 £ х₁ £ 1м)

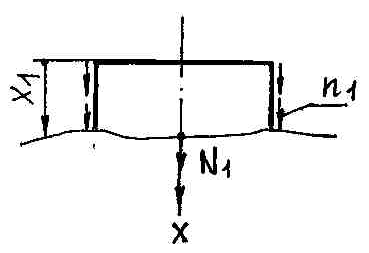åF_х= N₁ + n₁x₁ = 0

N₁ = – n₁x₁ = – 0.078 x₁

N₁(0) = 0, N₁(1м) = –0.078кН» –0.1кН ; s₁(0) = 0, s₁(1м) = – 0.1 Мпа

II участок: (0 £ х₂ £ 1.4м)

åF_х= F + n₁ℓ₁ + n₂x₂ + N₂ = 0

N₂ = –n₁ℓ₁ – F – n₂x₂ N₂(0) = – 10.1 кН, N₂(1.4м) = – 10.3 кН

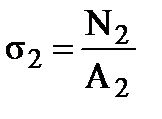s₂(0)= –5.04МПа, s₂(1.4м) = – 5.15МПа

III участок: (0 £ х₃ £ 1.6 м)

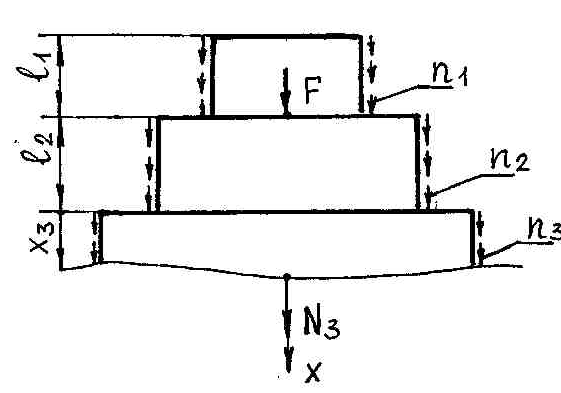åF_х=n₁ℓ₁+n₂ℓ₂+n₃x₃+N₃=0 N₃= – n₁ℓ₁ – F – n₂ ℓ₂ – n₃ x₃

N₃(0) = – 10.3 кН, N₃(1.6м) = – 10.6 кН 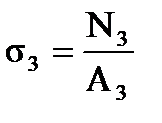σ ₃ (0) = – 4.29МПа, s₃(1.6) = – 4.42МПа

По найденным значениям строим эпюры продольной силы N и напряжения s.

При построении эпюр соблюдаются следующие правила:

1. эпюры строятся на базисных линиях; которые должны быть параллельны оси стержня;

2. ординаты эпюр откладываются перпендикулярно базисной линии;

3. на эпюрах в характерных точках проставляются числовые значения ординат; знак внутренних сил указывается в кружочке на площади эпюры;

4. эпюры штрихуются по нормали к базисной линии.

Рис.1.1.2

2. По эпюре нормальных напряжений определяем опасное сечение. Опасным является сечение, в котором нормальное напряжение принимает максимальное по абсолютной величине значение. В рассматриваемой задаче опасным является сечение D, в котором 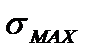=5,15МПа.

Условие прочности стержня при растяжении-сжатии:

Условие прочности выполняется.

3. Удлинение стержня при растяжении определяется по формуле:

,

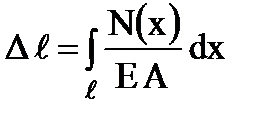где ℓ - длина стержня.

В случае, если продольная сила N и жесткость стержня ЕА постоянны по длине стержня, то

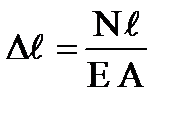
В данной задаче абсолютное удлинение стержня ℓ определяется как сумма удлинений отдельных участков:

Δℓ ₂ + Δℓ ₁ + Δℓ ₂ + Δℓ₃ , т.е.

Т.к. собственный вес колонны мал по сравнению с приложенной нагрузкой F, удлинение стержня Δℓ можно определить без учета собственного веса (n₁ = 0; n₂ = 0; n₃ = 0)

Δℓ =

Отрицательное значение Δℓ показывает, что стержень испытывает сжатие.

Дата добавления: 2014-11-18