Теоретична частина. Завдання для контрольної роботи

Завдання для контрольної роботи

Розрахувати магнітне поле в пристрої і тягове зусилля, прикладене до якоря при різних положеннях якоря в діапазоні зазорів між якорем і сердечником від 5 до 0,5 см з кроком 0,5 см. Побудувати залежність зусилля від положення електромагніту при живленні котушки постійним струмом.

Розміри електромагніту відповідно до рис. 3.1 приведені в таблиці. 2.

Рисунок 3.1 – Ескіз електромагніту.

Таблиця 2 – Розміри електромагніту.

№ варіанту	Розміри, см.
A	B	C	D	E	F	G	H	I
									0.1
									0.2
									0.3
									0.4
									0.1
									0.2
									0.3
									0.4
									0.1
									0.2
									0.3
									0.4
									0.1
									0.2
									0.3
									0.4

Відносна магнітна проникність повітря і котушки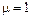

Щільність струму в обмотці j = 1,000,000 А/м2;

Крива намагнічення сердечника і якоря приведена в табл.3:

Таблиця 3 – Крива намагнічення.

H (А/м)
B (Tл)	0.80	0.95	1.00	1.10	1.25	1.40	1.55	1.65

У звіті потрібно відобразити:

1. Мета роботи

2. Початкові дані і геометричну модель

3. «Картину» поля при різних зазорах.

4. Отримані залежності зусиль від положення "якоря".

РЕКОМЕНДОВАНА ЛІТЕРАТУРА

1. ELCUT. Моделювання двовимірних полів методом кінцевих елементів. Версія 5.5. Керівництво користувача http://www.tor.ru/elcut/free_doc_r.htm

Розділ 1. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

1.1. Момент інерції

На відміну від поступального руху, де мірою інертності тіла є тільки його маса, у випадку обертального руху інертність тіла визначається як масою тіла так і розподілом маси відносно осі обертання. Тому для кількісної характеристики інертності тіл при їх обертальному русі вводиться фізична величина – момент інерції.

Моментом інерції тіла відносно деякої нерухомої осі OZє величина 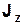, що визначається рівністю.

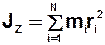. (1.1)

де _і – маса і -ї частинки тіла, яке умовно “розбивається” на N

частинок, настільки малих, що для кожної з них можна

однозначно вказати 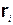- відстань частинки від осі OZ

Момент інерції тіла відносно осі дорівнює сумі добутків елементарних мас тіла на квадрати їх віддалей від осі обертання.

Зауважимо, що момент інерції існує незалежно від того, обертається тіло навколо деякої осі, чи перебуває відносно цієї осі у стані спокою.

Момент інерції - величина скалярна, вимірюється в кг·м².

Від (1.1) можна перейти до розрахунку інтеґралу:

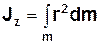. (1.2)

Якщо густина тіла 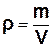- величина стала, то формула (1.2) набуде вигляду:

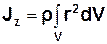. (1.3)

Використовуючи (1.3), можна розрахувати моменти інерції тіл правильної ґеометричної форми, зокрема:

· Момент інерції тонкостінного кільця товщиною b і радіусом основи R (R>>b) відносно його осі симетрії (ґеометричної осі):

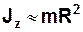. (1,4)

· Момент інерції суцільної кулі радіусом R відносно осі, що проходить через її центр:

. (1.5)

· Момент інерції тонкого стрижня з перерізом довільної форми відносно осі, що проходить через середину стрижня перпендикулярно до нього:

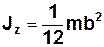, (1.6)

де b – довжина стрижня, набагато більша від його

максимального поперечного розміру.

·
Момент інерції суцільного однорідного циліндра відносно його ґеометричної осі:

Рис.1.1

Розділимо циліндр на окремі кільця безмежно малої товщини dr з внутрішнім радіусом r. Елементарний об’єм такого кільця:

. (1.7)

Підставивши (1.7) в (1.3), маємо:

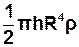= . (1.8)

Врахувавши, що:

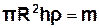- об’єм циліндра, - маса циліндра,

одержимо:

. (1.9)

1.2. Теорема Штайнера

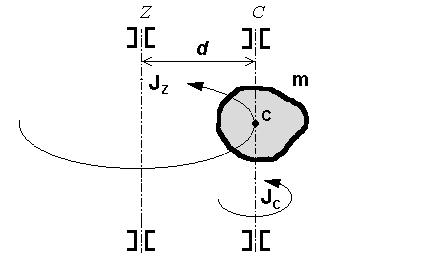
Якщо відомий момент інерції тіла відносно осі, яка проходить через його центр мас - 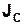, то момент інерції відносно осі, паралельної до вказаної – J_Z, визначається за теоремою Штайнера:

	Рис.1.2

Момент інерції тіла J_z відносно довільної осі дорівнює сумі моменту інерції J_С відносно осі, паралельної даній, що проходить через центр мас тіла і добутку маси тіла m на квадрат відстані між осями d.

. (1.10)

Дата добавления: 2014-11-18