Економіко-математичний аналіз оптимальних розрахунків

Економічну інтерпретацію двоїстої задачі розглянемо на прикладі оптимального використання обмежених ресурсів.

Для виробництва п видів продукції використовується т видів ресурсів, запаси яких обмежені значеннями b_і (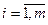). Норма витрат кожного виду ресурсу на одиницю продукції становить (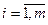; ). Дохід від одиниці продукції j -го виду дорівнює 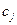( ). Знайти план виробництва продукції, що забезпечить максимальний сумарний дохід. Математична модель задачі:

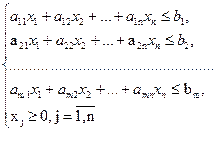
Пряма задача полягає у визначенні такого оптимального плану виробництва продукції Х_опт, який дасть найбільший дохід. Двоїста задача до окресленої задачі матиме вигляд:

Економічний зміст двоїстої задачі полягає в тому, щоб визначити таку оптимальну систему двоїстих оцінок у_i ресурсів, що використовуються для виробництва продукції, при яких загальна вартість усіх ресурсів буде найменшою. Оскільки двоїсті змінні означають цінність одиниці ресурсу, то їх інколи ще називають тіньовою ціною відповідного ресурсу.

За допомогою двоїстих оцінок можна визначити статус кожного ресурсу прямої задачі та рентабельність продукції, що виготовляється.

Ресурси, що використовуються для виробництва продукції, умовно можна поділити на дефіцитні та недефіцитні, залежно від того, повне чи часткове їх використання передбачено оптимальним планом прямої задачі. Якщо двоїста оцінка у_i в оптимальному плані двоїстої задачі дорівнює нулю, то відповідний і -тий ресурс при виробництві продукції повністю не використовується і є недефіцитним. Якщо ж двоїста оцінка y_і >0, то і -тий ресурс використовується повністю для оптимального плану виробництва продукції і називається дефіцитним. В цьому випадку величина двоїстої оцінки показує, наскільки збільшиться значення цільової функції Z, якщо запас відповідного ресурсу збільшити на одиницю.

Аналіз рентабельності продукції, що виготовляється, виконується за допомогою двоїстих оцінок і обмежень двоїстої задачі. Ліва частина кожного обмеження є вартістю всіх ресурсів, які використовуються для виробництва одиниці j -тої продукції. Якщо ця величина перевищує дохід від одиниці продукції (с_j), то виготовляти цю продукцію не вигідно, вона нерентабельна і в оптимальному плані прямої задачі відповідна х_j =0. Якщо ж загальна оцінка всіх ресурсів дорівнює доходу від одиниці продукції, то виготовляти таку продукцію доцільно, вона рентабельна і в оптимальному плані прямої задачі відповідна змінна х_j > 0.

ТЕМА 5. ТРАНСПОРТНА ЗАДАЧА

5.1 Постановка транспортної задачі та її математична модель.

5.2 Методи побудови початкового опорного плану.

5.3 Метод потенціалів.

5.4 Практичне застосування транспортної задачі. Модель оптимального розподілу фінансових ресурсів банку. Модель оптимізації штатного розпису фірми.

Дата добавления: 2014-11-18