О погрешностях измерений

Отсчет показаний

Главная деталь микрометра – точный микрометрический винт, ввернутый в гайку, называемую стеблем. При одном обороте винт перемещается вдоль своей оси на 0,5 мм. На винте неподвижно насажен барабан, на котором по окружности нанесено 50 делений. Таким образом, поворот винта на одно деление равен 1/50 полного оборота, или 0,01 мм (0.5мм/50 = 0,01 мм).

Таким образом, цена деления микрометра С = 0,01 мм = 10^-5 м, точность отсчета Δ х _пр. = ± 0,005 мм = ± 0,5•10^-5 м.

Виды измерений физических величин и их погрешностей

При измерении любой физической величины получить её абсолютно точное (истинное) значение невозможно из-за присутствующих всегда погрешностей измерений.

Различают прямые и косвенные измерения.

Измерение называют прямым, если значение измеряемой величины (например, длины или массы предмета) находят в результате сравнения с мерой этой же величины (измерительной линейкой, гирями определенной массы) или считываются со шкалы прибора, используемого для проведения наблюдения (например, вольтметра при измерении электрического напряжения).

Измерение называют косвенным, если значение измеряемой величины находят с помощью известной функциональной зависимости, которая связывает искомую величину с величинам, получаемыми непосредственно при прямых измерениях (например, сила электрического тока находится с помощью закона Ома по прямым измерениям электрического напряжения и сопротивления).

Все возможные погрешности измерений по характеру происхождения разделяют на три типа:

1. Грубая погрешность (промах) – чрезмерно большая погрешность, явно искажающая результат измерения.

Существует строгий математический способ определения ошибок подобного рода. Если подозрительное значение отличается от среднего более чем на 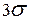( 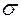- среднеквадратическое отклонение среднего, смысл этой величины и способ вычисления даны ниже), то считаем его грубой ошибкой и вычеркиваем.

Эта погрешность, связанная с невнимательностью или ошибкой экспериментатора, исключается из протокола измерений. Имеет смысл измерение повторить.

2. Систематическая погрешность – погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины.

Эта погрешность связана со сдвигом измеренного значения некоторой величины от её истинного значения. Если удается обнаружить причину или найти величину сдвига, то систематическую погрешность можно исключить введением поправки к измеренному значению величины. Однако, не существует универсальных правил, позволяющих найти систематическую погрешность данного измерения.

3. Случайные погрешности – погрешности, появление которых не может быть предупреждено.

Эти погрешности проявляются в разбросе отсчетов при повторных измерениях, проведенных в одних и тех же доступных контролю условиях, т.к. обусловлены факторами, меняющимися от измерения к измерению, действие которых на практике не всегда может быть учтено.

Выполнив измерение физической величины несколько раз, используя теорию погрешностей измерений, можно дать количественную оценку случайной погрешности и указать вероятность, с которой истинное значение измеряемой величины находится внутри некоторого интервала.

Методика статистической обработки результатов прямых измерений

Обозначим через 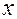измеряемую физическую величину. Пусть в результате нескольких опытов получено n пронумерованных значений 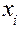(i – номер измерения, i = 1,2,3,…,n). Зададимся вопросом: Какую ошибку 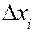мы допустили в каждом отдельном измерении? При известном истинном значение 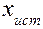, решение очевидно: .

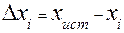Поскольку, 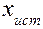нам не доступно, то его заменяют средним значением 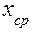, которое легко найти по известной формуле.

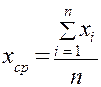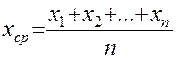или . (1)

Тогда, ошибка отдельного измерения (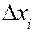) (несмотря на неизбежную небольшую неточность этих вычислений) легко вычисляется

(2)

Зная ошибку каждого измерения, следующим шагом найдем, так называемое среднеквадратическое отклонение среднего :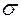

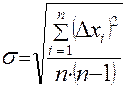или . (3)

(Внимание! Среднеквадратическое отклонение среднего 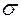вычисляют с точностью 10%-20%, не более 2 значащих цифр).

Формула для вычисления 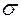доказывается в теории вероятности. Для практических целей существенное значение имеет её смысловое наполнение. Отложим на оси всевозможных 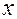, значения, , , .

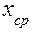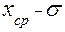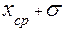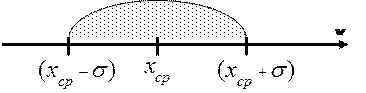Оказывается, что при проведении новых серий экспериментов, следующие средние значения 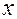будут попадать в интервал от (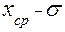) до (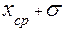) примерно 68 раз из 100. С точки зрения теории вероятности можно утверждать, что истинное значение 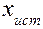лежит в интервале 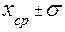с вероятностью 68%.

Вероятность , с которой среднее значение попадает в некоторый интервал, называется доверительной вероятностью, при этом интервал называют доверительным интервалом .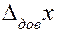

Однако 68% невысокая вероятность. В подавляющем большинстве случаев требуется знать интервал 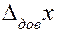с доверительной вероятностью = 90%, 95%, 98%. Найти его очень просто, если известны 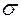и специальные коэффициенты Стьюдента 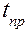, зависящие от числа измерений 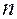и доверительной вероятности .

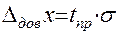(4)

Обработка случайных погрешностей прямых измерений сводится к нахождению 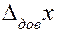с заданной доверительной вероятностью.

В лабораториях физики МГТУ принят государственный стандарт, в соответствии с которым = 0,95.

Таблица коэффициентов Стьюдента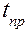

для доверительной вероятности = 0,95

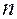
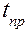
	12,3	4,3	3,18	2,78	2,6	2,26

Полная погрешность измерений 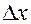складывается из доверительного интервала и инструментальной погрешности. Теория вероятности дает следующую формулу:

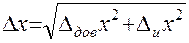(5)

Как только найдена полная ошибка, обработка погрешностей закончена. Записываем ответ:

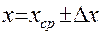, (6)

Рядом необходимо указать относительную погрешность

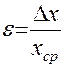, (7)

выраженную в процентах (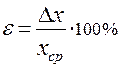) (8)

( Внимание! относительная погрешность ε превышающая 10%-15% свидетельствует о недостаточном усердии учащегося при выполнении лабораторной работы ).

Заметим, что 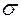и, следовательно, 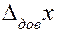вычисляют с точностью порядка 10%–20%. Поэтому при вычислении полной ошибки удобно пользоваться следующим правилом: если одна из ошибок 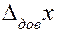или 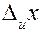превышает другую в 3 и более раз, то меньшей можно пренебречь.

Величину случайной погрешности можно уменьшить многократным повторением измерения. Использование теории случайных погрешностей оправдано лишь в том случае, если повторные измерения дают результаты, заметно отличающиеся друг от друга.

О точности измерительных приборов

Развитие измерительной техники привело к появлению разнообразных приборов, отличающихся своей точностью.

Точность прибора – это свойство измерительного прибора, характеризующее степень приближения показаний данного измерительного прибора к действительным значениям измеряемой величины.

Точность прибора либо задается классом точности[1] прибора, либо указана в паспорте, прилагаемом к прибору. Погрешность, вносимая прибором при каждом отдельном измерении (приборная погрешность, Δ х_пр.), связана с точностью прибора. Эта погрешность равна той доле деления шкалы прибора, до которой с уверенностью в правильности результата можно производить отсчет.

В тех случаях, когда класс точности не указан и нет указаний в паспорте прибора, приборная погрешность принимается равной половине цены наименьшего деления шкалы прибора: Δ х_пр. = ± 0,5 C, где С – цена наименьшего деления шкалы прибора.

В том случае, когда приборная и случайная погрешности сравнимы по величине, полную погрешность измерений можно представить в виде суммы двух составляющих: Δ х = Δ х_случ. + Δ х_пр..

Точность прибора невозможно превзойти никаким методом измерения на нем. Для более точных измерений применяют приборы более высокого класса.

Порядок операций при обработке результатов серии измерений

При прямых измерениях:

1. Результаты каждого измерения записать в таблицу.

2. Вычислить среднее значение из n измерений

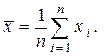
3. Найти погрешности отдельных измерений

.

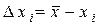4. Вычислить квадраты погрешностей отдельных измерений

(D x ₁)², (D x ₂)²,..., (D x_n)².

5. Оценить среднеквадратичную погрешность среднего значения

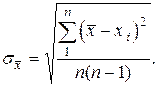
6. Определить коэффициент Стьюдента t _na (по таблице) для доверительной вероятности Р = 0,95 и числа произведенных измерений n.

7. Найти случайную погрешность результата измерений:

.

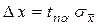8. Если случайная погрешность результата измерений D x окажется сравнимой* с систематической (погрешностью прибора D x _пр), то в качестве погрешности результата измерений следует взять величину

.

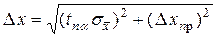9. Окончательный результат записать в виде:

.

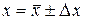10. Оценить относительную погрешность результата измерений

.

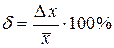При косвенных измерениях:

1. Для каждой непосредственно измеренной величины (X ₁, X ₂,..., X _m), входящей в расчетную формулу для определения X (X = f (X ₁, X ₂,..., X _m)), провести обработку в описанной выше последовательности, т.е. вычислить средние арифметические значения 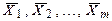по формуле (1) и случайные погрешности D X ₁, D X ₂,..., D X _m по формуле (4) для доверительной вероятности Р = 0,95.

2. При необходимости учесть систематическую (приборную) погрешность каждой серии измерений

,

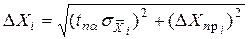где индекс i относится к соответствующей измеренной величине, а D X _{пр i} – систематическая погрешность прибора, используемого для измерения Х_i.

3. Вычислить наиболее вероятное значение X:

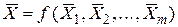
4. Вычислить частные производные 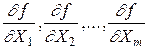при средних значениях величин X ₁, X _2, ..., X_m.

5. Определить абсолютную погрешность косвенного измерения X по общей формуле:

.

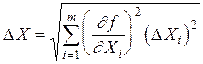Здесь и выше m – число независимых непосредственно измеренных величин.

6. Записать окончательный результат в виде

.

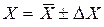7. Определить относительную погрешность косвенного измерения X:

.

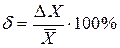Правила представления результата измерения

Все результаты измерений, а также вычисленный по ним окончательный результат приводят вместе с погрешностью, которую выражают в тех же единицах, что и саму измеряемую величину, например: l = (1,572 ± 0,004) м.

Среднее значение < x> необходимо округлять так, чтобы оно оканчивалось цифрой того же разряда, что и Δ х после её округления. Т.е. число и его погрешность всегда записывается так, чтобы их последние цифры принадлежали одному и тому же десятичному разряду. Значения погрешностей следует округлять, оставляя одну значащую цифру[2]. Округлять предпочтительно в сторону большего значения.

Примеры:

1. Получено: U = 124,4 В; Δ U = 1,1 В.

Следует записать: U = (124,0 ± 1,0) В.

2. Получено: V = 2,678•10³ см/с; Δ V = 1,2 см/с.

Следует записать: V = (2,678 ± 0,001)•10³ cм/с.

В промежуточных выкладках при расчете погрешностей нужно удерживать три-четыре значащие цифры.

При представлении окончательных результатов физических измерений часто применяют запись числовых значений в виде десятичной дроби, умноженной на необходимую степень числа десять.

Примеры:

1. При обработке группы результатов измерений получены:
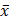= 965,332 и Δ х = 8,35.

Результат округления записывают в виде: х = 965 ± 8.

2. При обработке группы результатов измерений получены:
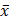= 0,003893 и Δ х = 0,000282.

Результат округления записывают в виде: х = (38,9 ± 2,8)•10⁴.

3. Числа 3106; 0,0285; 0,120 записывают так:

3,106•10³; 2,85•10^-2; 1,2•10^-1.

Графическое представление результатов измерений

В большинстве лабораторных работ требуется представить результаты в виде различного рода графиков. Их правильное построение требует соблюдения несложных правил.

1. Масштабы и начала отсчета по координатным осям выбираются так, чтобы график изображения зависимости занимал большую часть поля чертежа. При этом на пересечении осей не обязательно должны находиться нулевые значения величин.

Дата добавления: 2014-11-18