В умовах природного залягання

НАПРУЖЕНИЙ СТАН ГІРСЬКИХ ПОРІД

Напружений стан гірських порід в земній корі зумовлений тиском розташованих вище порід і тектонічними процесами.

Розглянемо випадок, коли напружений стан масиву порід зумовлений лише гравітаційними силами, тобто дією ваги порід, розташованих над розглядуваною точкою масиву. Для визначення напружень в будь-якій точці уявно виріжмо елементарний куб довкола цієї точки (рис. 7.1).

Замінимо дію відкинутих частин масиву напруженнями на гранях куба, котрі розкладемо по напрямах, паралельних до осей координат. Напруження, перпендикулярні до граней куба, називаються нормальними і позначаються σ, а ті, що діють в площині грані – дотичними і позначаються τ з відповідними індексами, як показано на рис. 7.1

З умови рівноваги елементарного куба можна записати, що

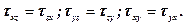
Таким чином, напружений стан в точці визначається шістьма компонентами напруження: σ_x; σ_y; σ_z; Якщо орієнтацію граней елементарного куба підібрати таким чином, щоб , то грані куба утворять головні площадки, а відповідні нормальні напруження – головні нормальні напруження, які позначаються σ₁; σ₂; σ₃, причому

Сума нормальних напружень, що діють в трьох взаємно перпендикулярних напрямах, є величина постійна і називається гідростатичним тиском у точці:

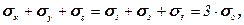(7.1)

де σ₀ – середнє нормальне напруження (гідростатичний тиск).

Аналогічно нормальним напруженням розглядаються головні дотичні напруження, які діють на площадках, що ділять пополам кут між двома відповідними напруженнями і проходять через третє головне напруження.

Їх величину можна визначити за формулами:

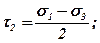(7.2)

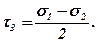
Розглянемо випадок, коли напружений стан масиву порід зумовлений лише гравітаційними силами, тобто дією ваги порід, розташованих над розглядуваною точкою масиву. При відсутності тектонічних рухів на ділянці земної кори напружений стан гірських порід, симетричний відносно вертикалі, що дає змогу представити його двома компонентами в циліндричній системі координат:

і

Вертикальні напруження σ_z в точці М пружного ізотропного масиву зумовлені вагою розташованих вище порід

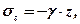(7.3)

де γ – середня об’ємна вага розташованих вище порід;

z – глибина залягання розглядуваної точки від земної поверхні.

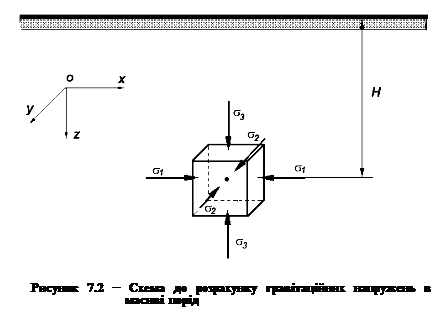
Розглянемо умову рівноваги уявно виділеного елементарного куба з ребрами одиничної довжини, розташованими вертикально і горизонтально (див. рис. 7.2).

Цей куб стиснутий вертикальною гравітаційною силою σ₃₌s_z, під дією якої він намагається стати коротшим у вертикальному напрямі і розширитися в горизонтальних напрямах. Але цьому розширенню протидіє реакція оточуючих порід. Останні тиснуть на вертикальні грані елементарного куба з реактивними силами, спрямованими перпендикулярно цим граням по осях Оx і Oy. В результаті в кубі виникають стискуючі радіальні напруження ().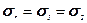

Для визначення напружень σ_r визначимо зміну довжини ребра елементарного куба в напряму осі Ох. Якби на куб діяла лише вертикальна сила гравітації 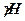, то горизонтальне ребро куба видовжилося б на величину:

(7.4)

де μ – коефіцієнт поперечних деформацій (коефіцієнт Пуассона);

Е – модуль поздовжньої пружності породи.

Але крім того, стиснення від тиску оточуючих порід σ_r в напряму осі Oy спричинює видовження ребра куба вздовж осі Ox на величину:

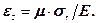(7.5)

Тиск оточуючих порід σ_r намагається зменшити довжину ребра куба вздовж осі Ox на величину:

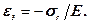(7.6)

Загальна зміна довжини куба вздовж осі Ox складає

(7.7)

Однак сусідні частини гірської породи не дозволяють ребру деформуватися в горизонтальному напрямку Ox. Тому, прирівнявши рівняння (7.7) до нуля, отримуємо умову

З цієї умови, підставивши в нього значення σ_z з виразу (7.3), отримуємо формулу Динника Н.А. для пружно напруженого стану гірських порід

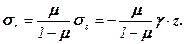(7.8)

В загальному випадку

(7.9)

Величина λ називається коефіцієнтом бокового розпору. Він показує, яку частку абсолютної величини активного навантаження складають реактивні сили, котрі діють в площині, перпендикулярній до напрямку активного навантаження, за умови, що деформування порід в масиві неможли ве.

В розглядуваному випадку активними є напруження, зумовлені силами гравітації, тобто напруження σ_z, спрямовані вертикально вниз; реактивними є радіальні напруження σ_r.

В результаті релаксації відбувається вирівнювання напружень в земній корі, тобто . В більшості випадків можна прийняти умови і . Це означає, що гірські породи знаходяться в умовах рівномірного усестороннього стиску.

Природні напруження в земній корі прийнято називати гірським тиском.

Вертикальну складову гірського тиску називають геостатичним або повним гірським тиском, а горизонтальну складову – боковим тиском.

Для тектонічно спокійних регіонів геостатичний тиск на глибині z визначають за формулою

, (7.10)

де ρ_п і ρ_ф – відповідно мінералогічна густина порід і густина флюїду як функції глибини;

П – пористість порід як функція глибини;

g – прискорення вільного падіння.

В інженерних розрахунках гірський тиск визначають дискретно по інтервалах (товщах) літологічно однорідних порід.

Градієнт геостатичного тиску

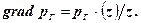(7.11)

Пористі гірські породи або породи-колектори, якими є більшість осадових порід, завжди насичені рідиною або газом. Тиск порової рідини прийнято називати пластовим тиском у випадку відкритої пористостіі поровим тиском у випадку ізольованої пористості.

Тобто термін “поровий тиск ” на відміну від пластового застосовують для пластів, складених практично непроникними гірськими породами (наприклад, глинами).

В нормальних умовах величина пластового тиску p_П приблизно дорівнює гідростатичному тиску води

(7.12)

Градієнт grad p_П і коефіцієнт аномальності пластового тиску k_a знаходять за формулами:

; (7.13)

, (7.14)

де z – глибина залягання пласта;

ρ_в – густина прісної води.

В ряді випадків пластові тиски характеризуються відхиленням від нормального в будь-яку сторону (k_a≠1).

Аномально низькі (АНПТ) і аномально високі (АВПТ) пластові тиски зумовлені рядом факторів, пов’язаних з геологічною будовою району залягання порід. На великих глибинах АНПТ зустрічаються рідше.

Основні причини проявлення АНПТ (k_a<1):

– часткове розвантаження гірського тиску, що є причиною збільшення порового простору;

– велика альтитуда устя свердловини, більша за рівень ґрунтових вод;

–некомпенсований відбір флюїду з пласта при експлуатації свердловини.

Нормальний пластовий тиск виникає в гідравлічно відкритій системі, в якій відбір флюїду компенсується припливом з області “живлення ”.

На противагу цьому пласти з АВПТ є гідравлічно закритою системою, тобто нормальні і аномальні пластові тиски співіснують лише в тому випадку, якщо вони розділені бар’єром тиску. Бар’єр тиску заважає проходженню через нього великих об’ємів флюїду і може бути фізичного, хімічного і змішаного походження. В літологічному відношенні бар’єр тиску представлений породами-неко­лекторами (глинами, алевролітами, солями та ін.).

Наявність зон АВПТ (k_a>1) пов’язана з геологічними, геохімічними і механічними процесами: в результаті локальних і регіональних тектонічних рухів; швидкості седиментації і умов накопичення відкладів; діагенезом, пов’язаним з утворенням нових мінералів чи перекристалізацією речовини у відкладах; за рахунок осмотичних явищ; за рахунок гідравлічного зв’язку з глибоко залеглими пластами, що мають підвищений тиск тощо.

Розглянемо вплив тиску рідини в порах на напружений стан скелету пористої гірської породи, для чого розглянемо ідеальну модель твердого пористого тіла і виріжмо з неї одиничний елемент (рис 7.3).

Зверху на одиничну площадку діє геостатичний тиск

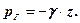(7.15)

Якби увесь вертикальний тиск сприймався скелетом породи, то напруження в скелеті в січенні І-І було б максимальним

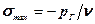. (7.16)

Тут n – частка одиничної площадки, яку займає скелет в розглядуваному січенні.

Але рідина, що знаходиться в порах, сприймає навантаження, рівне .

Тому напруження в скелеті дорівнює:

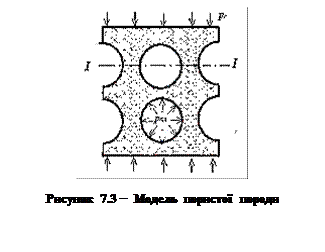(7.17)

Позначимо , тоді

(7.18)

Величина h залежить від пористості і структури порового простору. З формули (47) видно, що із збільшенням пластового тиску вертикальне навантаження на скелет зменшується.

Якщ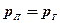о , то

Отже, по мірі наближення пластового тиску до геостатичного напружений стан скелету буде прагнути до рівномірного усестороннього стиску.

Рівномірний усесторонній стиск

Усесторонній стиск називають рівномірним, якщо виконується умова . В цьому випадку дотичні напруження дорівнюють нулю. З третьої і четвертої теорій міцності випливає, що яким би великим не було середнє напруження (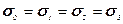), в гірській породі не можуть виникнути ні залишкові деформації, ні відбутися її руйнування. Гірська порода деформується лише пружно відповідно до закону Гука.

Ці висновки добре підтверджуються при випробуванні щільних однорідних порід і породоутворюючих мінералів. При деформуванні пористих гірських порід спостерігаються не лише залишкові деформації, але і їх руйнування, оскільки напружений стан скелету породи суттєво відрізняється від рівномірного усестороннього стиску. Таким чином, можна підсумувати, що при рівномірному усесторонньому стику породоутворюючі мінерали і щільні породи можуть деформуватися лише пружно, а в пористих гірських породах крім пружних деформацій можливе ще й ущільнення за рахунок зменшення об’єму пор.

При рівномірному усесторонньому стиску випробування порід і мінералів проводять для вивчення їх стискуваності, яка характеризується коефіцієнтом об’ємного стиску і об’ємним модулем пружності.

Під коефіцієнтом об’ємного стиску β розуміють відносне зменшення об’єму V із зменшенням тиску на 10⁵ Па, тобто

(7.19)

де V₀ – початковий об’єм при нормальних тиску і температурі.

Якщо при деформуванні зберігається закон Гука, то

(7.20)

Підставивши (50) у вираз (49), отримаємо

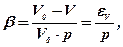(7.21)

а так як 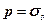, то , де K – об’ємний модуль пружності, який визначають за формулою (16).

Із збільшенням тиску коефіцієнт β для мінералів за виключенням польових шпатів, слюди, кам’яної солі і кварцу практично не змінюється.

У гірських порід коефіцієнт β зменшується. Це пояснюється тим, що в породах із збільшенням тиску зростає кількість і поверхня контактів між окремими зернами, тобто відбувається ущільнення структури.

Коефіцієнт β у порід завжди більший або дорівнює середньому коефіцієнту стискуваності мінералів, з яких вони складаються. Стискуваність породи залежить від стискуваності складових мінералів та інтенсивності взаємодії в місцях контактів між зернами цих мінералів. Цим пояснюється, наприклад, висока стискуваність гранітів, у яких породоутворюючі мінерали – кварц, польові шпати, слюда – мають вищі за інші мінерали значення β.

Нерівномірний усесторонній стиск

З точки зору стійкості а також руйнування гірських порід, з яких складаються стінки гірничих виробок, найцікавішим є випадок нерівномірного усестороннього стиску, який має місце, коли хоча б одне з головних напружень не дорівнює двом іншим. В загальному випадку має місце умова

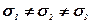(7.23)

Закономірності деформування порід в умовах нерівномірного усестороннього стиску досліджувало багато вчених (Байдюк, Шрейнер, Сеїд-Рза, Співак). Розглянемо результати цих досліджень. Результати випробувань мають вигляд залежностей 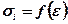при певних значеннях початкової величини середнього тиску p. Узагальнений вигляд залежності 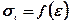подано на рис. 7.4.

На відрізках 0 а₁, 0 а₂, 0 а₃, 0 а₄ виконується закон Гука. На відрізках a₂ b₂, a₃ b₃, a₄ b₄ має місце перехідний процес, котрий закінчується або сталим пластичним деформуванням (відрізки b₂ с₂, b₃ с₃, b₄ с₄), або крихким руйнуванням (відрізок a₁ c₁).

Якщо пластичні зсуви локалізуються в певних зонах зразка, то розвиток деформування супроводжується зменшенням σ_і і закінчується руйнуванням зразка. В цьому випадку модуль пластичності або дорівнює нулю, або є від’ємним.

Рисунок 7.4 − Узагальнений вид залежностей s_і від e при різних значеннях початкового усестороннього стиску | p₁ |<| p₂ |<| p₃ |<| р₄ |

Якщо пластичні зсуви рівномірно розподілені по зразку, то має місце зміцнення, тобто розвиток деформування спостерігається лише при зростаючому напруженні (відрізок b₄ c₄). Але і цей процес закінчується другою перехідною зоною c₄ d₄ і далі – локалізацією деформації і руйнуванням.

Величина напружень, що відповідає точкам a₁, a₂, a₃ і a₄ позначається s_is і називається межею текучості породи.

Величина напружень, що відповідає умові називається міцністю породи і позначається s_{іс .}

З рис. 7.4 видно, що із збільшенням усестороннього стиску зростають як межа текучості, так і міцність породи.

Крім того, спостерігається і зміна процесу пластичного деформування породи (від крихкого руйнування до деформування із зміцненням). Пластичне деформування в гірських породах може відбуватися як за рахунок ковзання всередині зерен кристалів, так і за рахунок міжкристалічного ковзання. Останнє є переважаючим.

Величина пластичної деформації в гірських породах залежить від тиску і зростає з його збільшенням. Із зростанням пластичної деформації безперервно зростає зміцнюваність, яка є неодмінним наслідком пластичної деформації.

Дата добавления: 2014-11-18