Втискування плоского циліндричного індентора

Плоский циліндричний штамп втискується в пружний на півпростір силою Р, що діє по осі Z (рис. 10.5).

Задача осесиметрична, тому її розв’язок дається в циліндричних координатах (за­дача Чаплигіна–Садовського).

Розподіл тиску по площі круга описується рівнянням 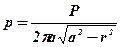, (10.6)

(а – радіус штампа).

Проаналізувавши формулу (83), бачимо, що при r = 0

(10.7)

а якщо r = a, то p = ¥.

Тобто розподіл напружень на площі контакту нерівномірний: мінімальні на­пруження p=0,5p_c мають місце в центрі, максимальні – на контурі контакту – досягають безмежної величини (p_c – середній тиск).

Остання обставина в дійсності неможлива, оскільки величина напруження обмежена межею текучості для пластичних порід і межею міцності для крих­ких порід.

Експериментальними роботами Шрейнера Л.А. та ін. встановлено, що розподіл напружень на площі контакту нерівномірний лише на початку втискування, пізніше його можна прийняти як рівномірно розподілений, тобто

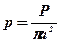. (10.8)

Переміщення штампа для випадку нерівномірного розподілу тиску визначають за формулою

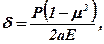(10.9)

а при рівномірному розподілі:

(10.10)

де m – коефіцієнт Пуассона;

Е – модуль Юнга.

Барон Л.І. проаналізував напружений стан пружного півпростору при втискуванні жорсткого штампа для умови рівномірного розподілу напруження по площадці контакту.

Під штампом розташована область І усестороннього стиску, обмежена поверхнею s_x = 0 (рис. 10.5). Розміри цієї області визначаються радіусом площадки контакту і коефіцієнтом Пуассона. Область І усестороннього стиску оточена областю ІІ, де одне з головних напружень більша за нуль (розтягуюче). Область ІІ знизу обмежена поверхнею s_y = 0. Далі розташована область ІІІ, де s_x >0 і s_у >0.

Для оцінки співвідношення величин s_x, s_y, s_z розглянемо, як змінюються головні напруження під штампом на осі симетрії Z (рис. 10.6).

На поверхні контакту усі головні напруження рівні між собою (має місце рівномірний усесторонній стиск). З віддаленням від поверхні контакту стискуючі напруження зменшуються, особливо s_x і s_y, які на деякій глибині переходять в розтягуючі. Однак величина розтягуючих напружень не перевищує 10% від величини нормального тиску. Оскільки боковий тиск практично завжди менший за гірський, із збільшенням глибини рівномірний стиск змінюється на нерівномірний усесторонній стиск (s_z¹s_{x, y}). Як результат, виникають дотичні напруження. Вони спочатку зростають, досягаючи максимуму на глибині, що дорівнює радіусу штампа, а потім зменшуються, прямуючи до нуля.

Таким чином, при втискуванні плоского циліндричного штампа найімовірнішими місцями зародження тріщин і руйнування є: на поверхні периферійна зона контакту, а в масиві – область на глибині, рівній радіусу індентора.

Дата добавления: 2014-11-18