Деформування і руйнування гірських порід

Основні принципи і схеми вивчення динамічного

РУЙНУВАННЯ ГІРСЬКИХ ПОРІД ПРИ ДИНАМІЧНОМУ ВТИСКУВАННІ

Класифікація гірських порід

За результатами експериментального дослідження властивостей гірських порід при втискуванні штампа у значну кількість зразків гірських порід було створено кілька класифікаційних шкал за окремими механічними властивостями.

Класифікаційна шкала за твердістю. Усі породи за твердістю за штампом розділено на три групи: м’які, середні, тверді. Кожна група в свою чергу розділена на чотири категорії, тобто прийнято всього дванадцять категорій твердості (табл. 10.1).

До І групи переважно належать породи сильно пластичні і дуже пористі. З порід, що зустрічаються при бурінні нафтових і газових свердловин. До цієї групи належать глинисті породи, аргіліти, найбільш пористі різновиди пісковиків та вапняків.

До ІІ групи за твердістю належать в основному породи з класу пластично-крихких, зокрема – алевроліти, вапняки, ангідрити, доломіти і пісковик

До ІІІ групи порід за твердістю відносяться переважно породи з класу крихких. Це переважно вивержені і метаморфічні породи. З порід, що зустрічаються при бурінні нафтових і газових свердловин, до цієї групи входять кремені, кварцити, різновиди скременілих вапняків і пісковиків.

Класифікаційна шкала, наведена в табл. 10.1, співпадає з класифікацією, прийнятою в практиці буріння.

Класифікаційна шкала за модулем Юнга. За модулем Юнга усі гірські породи розділені на вісім категорій (табл. 10.2).

Класифікаційна шкала за пластичністю. За величиною коефіцієнта пластичності гірські породи розділені на шість категорій (табл. 10.3).

До першої категорії належать крихкі породи, з другої до п’ятої – пластично-крихкі, а до шостої сильно пластичні і дуже пористі.

Слід відзначити, що для гірських порід, спостерігається значний розкид величин механічних характеристик. Це пояснюється тим, що механічні властивості окремих груп впливає не тільки мінералогічний склад, але і їх внутрішня будова.

Таблиця 10.1 – Класифікація гірських порід за твердістю

Група	І (м’які)	ІІ (середні)		ІІІ (тверді)
Категорія
Твердість за штампом, МПа	<100	-	-	-1000	-1500	-2000	-3000	3000-	-5000	-6000	6000-7000	>7000

Таблиця 10.2 – Класифікація гірських порід за модулем Юнга

Категорія
Коефіцієнт пластичності		1-2	2-3	3-4	4-6
Клас порід	пружно-крихкі	пружно-пластичні	сильно пластичні і дуже пористі

Таблиця 10.3 – Класифікація гірських порід за пластичністю

Категорія
Модуль Юнга, МПа	<2500	2500-	-	10000-	25000-	50000-	75000-	>100000

При бурінні свердловин мають місце виключно динамічні процеси. Якщо для опису статичних процесів достатня система рівнянь рівноваги сил і моментів, то для динамічних процесів додатково потрібно мати рівняння балансу енергії. Динамічні процеси є складнішими і не можуть бути вивченими в статичних умовах.

З точки зору буріння слід вивчати динамічне прикладення навантаження з боку елементів озброєння долота до гірської породи. При цьому слід мати на увазі, що ці процеси призводять до пластичного деформування і крихкого руйнування породи. Вони не піддаються єдиному математичному описові, і при їх вивченні основну роль відіграють експериментальні дослідження.

При експериментальному вивченні динамічного деформування і руйнування порід застосовуються принципи наближеного моделювання, котрі реалізуються на спеціальних установках. Найширше використовуються установки двох типів: копрові і кулачкові. На копрових установках використовується удар вільно падаючого ударника, або ударника, який розганяється прикладеною силою, наприклад тиском повітря. На кулачкових установках задається закон руху породруйнуючого елемента відносно породи, що дає змогу повніше моделювати процес його взаємодії з породою.

Строгий математичний опис процесу взаємодії породоруйнуючих елементів з гірською породою можна дати лише для найпростіших випадків.

Перший випадок. По поверхні породи, яка є пружним півпростором, здійснюється удар жорстким ударником масою m, який вільно падає. На момент контакту швидкість руху ударника v=v₀, а прикладена до нього сила Р дорівнює нулю в процесі усього деформування (рис 11.1). Кінетична енергія вантажу, що падає, на початок контактування з пружним тілом

(11.1)

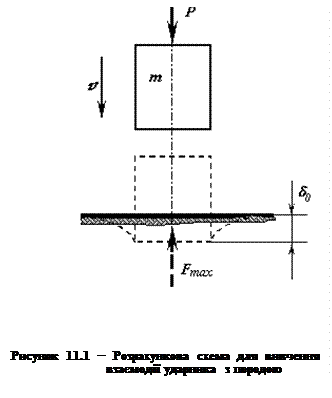Опір поверхні породи спричинює гальмування тіла, котре падає. Сила взаємодії при пружному деформуванні прямо про­порційна зміщенню поверхні d

, (11.2)

де К – коефіцієнт пропорційності, який залежить від пружних властивостей гірської породи і форми робочої поверхні ударника.

Максимальною сила взаємодії буде при максимальному зміщенні поверхні (d₀), тобто в момент, коли швидкість руху ударника зменшиться до нуля.

При цьому потенціальна енергія деформування складе

, (11.3)

або з урахуванням виразу (11.2)

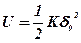. (11.4)

З умови U = U_к можна визначити максимальне зміщення поверхні

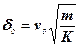, (11.5)

і далі найбільшу силу взаємодії

. (11.6)

Другий випадок. Розглянемо ту ж задачу при P=const. Тоді баланс енергії при d=d₀ запишеться в вигляді

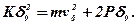(11.7)

Розв’язок рівняння (11.7) має вигляд

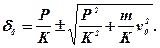(11.8)

Враховуючи фізичний смисл процесу, приймаємо знак плюс. Підставивши значення d₀ у вираз (11.2), визначимо максимальну силу взаємодії

(11.9)

Якщо v₀=0, то F_{ma x}= 2P, тобто має місце так звана несподівана взаємодія (миттєве прикладення навантаження).

Дата добавления: 2014-11-18