Предел и непрерывность функции двух переменных

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывность, аналогично случаю функции одной переменной.

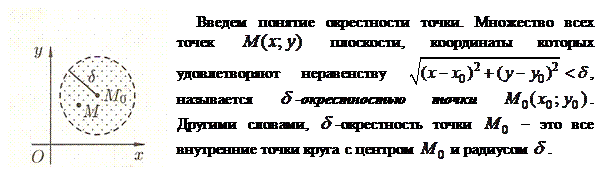
Пусть функция 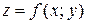определена в некоторой окрестности точки , кроме, может быть, самой этой точки.

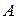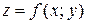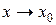Определение 1.3. Число называется пределом функции при и 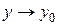(или, что то же самое, при 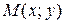® ), если для любого существует такое, что для всех и 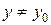, и удовлетворяющих неравенству выполняется неравенство 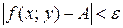. Записывают:

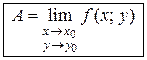
или

.

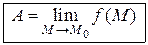Из определения следует, что если предел существует, то он не зависит от пути, по которому стремится к (число таких направлений бесконечно). Определения бесконечно малых и бесконечно больших величин являющихся функциями двух переменных, аналогичны соответствующим определениям для функций одной переменной.

Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной.

Определение 1.4. Функция 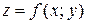(или 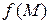) называется непрерывной в точке , если она:

1) определена в этой точке и некоторой ее окрестности;

2) имеет предел ;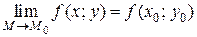

3) этот предел равен значению функции в точке , т.е.

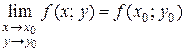или .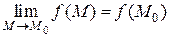

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва 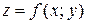могут образовывать целые линии разрыва. Так, например, функция имеет линю разрыва .

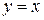Можно дать другое, равносильное приведенному выше, определение непрерывности функции 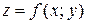в точке. Обозначим 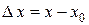, 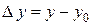. Значит, и . Величины 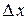и 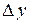называются приращениями аргументов 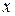и . Тогда . Величина называется полным приращением функции 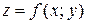в точке .

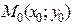Определение 1.5. Функция 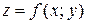называется непрерывной в точке 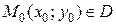, если полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов 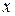и стремится к нулю, т.е.

.

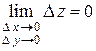Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям – подобные теоремы имели для функций одной переменной.

Дата добавления: 2014-11-18