Предикаты и операции над ними

В математике часто встречаются предложения, содержащие одну или несколько переменных, например: «х + 2 = 7», «город стоит на Волге». Эти предложения не являются высказываниями, т.к. о них нельзя сказать, истинны они или ложны. Однако при подстановке конкретных значений переменной х они обращаются в истинные или ложные высказывания. Так, в первом примере при х = 5 получаем истинное высказывание, а при х = 3 – ложное высказывание.

Определение. Предложение с переменными, которое при конкретных значениях переменных обращается в высказывание, называется высказывательной формой или предикатом.

По числу входящих в предикат переменных различают одноместные, двухместные и т.д. предикаты и обозначают А (х), В (х;у)…

Пример: А (х): «х делится на 2» – одноместный предикат, В (х; у): «прямая х перпендикулярна прямой у» – двухместный предикат.

Следует иметь в виду, что в предикате переменные могут содержаться неявно: «число делится на 2», «студент получил отличную оценку на экзамене по математике».

Задание предиката, как правило, предполагает и задание множества, из которого выбираются значения переменных, входящих в предикат.

Определение. Множеством (областью) определения предиката называется множество Х, состоящее из всех значений переменных, при подстановке которых в предикат последний обращается в высказывание.

Так, предикат «х > 2» можно рассматривать на множестве натуральных чисел или действительных чисел.

Каждый предикат А (х), х Î Х определяет множество Т Ì Х, состоящее из элементов, при подстановке которых в предикат А (х) вместо х получается истинное высказывание.

Определение. Множество, состоящее из всех тех значений, при подстановке которых в предикат получается истинное высказывание, называется множеством истинности предиката (обозначается Т).

Пример. Рассмотрим предикат А (х): «х < 5», заданный на множестве натуральных чисел. Т = {1; 2; 3; 4}.

Предикаты, как и высказывания, бывают элементарными и составными. Составные предикаты образуются из элементарных при помощи логических связок.

Пусть Т_А – область истинности предиката А (х), Т_В – область истинности предиката В (х).

Определение. Конъюнкцией предикатов А (х) и В (х) называется предикат А (х) Ù В (х), который истинен для тех и только тех значениях х Î Х, для которых оба предиката истинны.

Покажем, что Т_{А Ù В} = Т_А Ç Т_В.

Доказательство. 1) Пусть а Î Т_{А Ù В} Þ А (а) Ù В (а) – истинное высказывание. По определению конъюнкции имеем: А (а) – истинно, В (а) – истинно Þ а Î Т_А Ù а Î Т_В Þ а Î Т_А Ç Т_В Þ Т_{А Ù В} Ì Т_А Ç Т_В.

2) Пусть b Î Т_А Ç Т_В Þ b Î Т_А Ù b Î Т_В Þ А (b) – истинно, В (b) – истинно Þ по определению конъюнкции А (b) Ù В (b) – истинное высказывание Þ b Î Т_{А Ù В} Þ Т_А Ç Т_В Ì Т_{А Ù В} .

Т.к. Т_{А Ù В} Ì Т_А Ç Т_В и Т_А Ç Т_В Ì Т_{А Ù В} , то по свойству равенства множеств Т_{А Ù В} = Т_А Ç Т_В, что и требовалось доказать.

Заметим, что полученное правило справедливо и для предикатов, содержащих более одной переменной.

Пример. Рассмотрим предикаты А (х): «х < 10», В (х): «х делится на 3», заданные на множестве натуральных чисел. Найдем область истинности предиката А (х) Ù В (х): «х < 10 и делится на 3».

Т_А = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}, Т_В = {3; 6; 9; 12; 15; …}, тогда Т_{А Ù В} = {3; 6; 9}.

Определение. Дизъюнкцией предикатов А (х) и В (х) называется предикат А (х) Ú В (х), который истинен для тех и только тех значениях х Î Х, для которых истинен хотя бы один из предикатов.

Можно доказать (самостоятельно), что Т_{А Ú В} = Т_А È Т_В.

Пример. Рассмотрим предикаты А (х): «х делится на 2», В (х): «х делится на 3», заданные на множестве натуральных чисел. Найдем область истинности предиката А (х) Ú В (х): «х делится на 2 или на 3».

Т_А = {2; 4; 6; 8; 10;…}, Т_В = {3; 6; 9; 12; 15; …}, Т_{А Ú В} = {2; 3; 4; 6; 8; 9; …}.

Определение. Отрицанием предиката А (х)называется предикат . Он истинен для тех и только тех значениях х Î Х, для которых предикат А (х) ложен и наоборот.

Заметим, что = .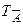

Определение. Импликацией предикатов А (х) и В (х) называется предикат А (х) Þ В (х) (читают: «Если А (х), то В (х)»). Он обращается в ложное высказывание при тех значениях х Î Х, для которых предикат А (х) истинен, а предикат В (х) ложен.

Из определения имеем, что предикат А (х) Þ В (х) ложен на множестве Т_А Ç 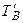, а следовательно истинен на дополнении к этому множеству. Воспользовавшись законами операций над множествами, имеем: .

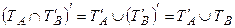Контрольные вопросы

1. Что называется высказывательной формой или предикатом?

2. Какие различают предикаты по числу входящих в них переменных? Приведите примеры.

3. Какое множество называют областью определения предиката?

4. Какое множество называют множеством истинности предиката?

5. Что называют конъюнкцией предикатов? Докажите равенство, связывающее область истинности конъюнкции предикатов с областями истинности этих предикатов.

6. Дайте определения дизъюнкции, отрицания, импликации предикатов. Запишите равенства, связывающие области истинности конъюнкции предикатов с областями истинности этих предикатов.

Дата добавления: 2014-11-18