
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функції. Асимптоти лінії
|
|
|
|
Розділ 12. ОПУКЛІСТЬ І ВГНУТІСТЬ графіка
12.1. Поняття опуклості і вгнутості графіка функції.
Розглянемо на площині рафіком диференційованої функції 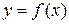 .
.
Означення 12.1. Крива називається опуклою на інтервалі 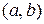 , якщо всі точки кривої з цього інтервалу лежать нижче будь-якої її дотичної проведеної на цьому інтервалі.
, якщо всі точки кривої з цього інтервалу лежать нижче будь-якої її дотичної проведеної на цьому інтервалі.
 Означення 12.2. Крива називається вгнутою на інтервалі
Означення 12.2. Крива називається вгнутою на інтервалі  , якщо всі точки кривої з цього інтервалу лежать вище будь-якої її дотичної проведеної на цьому інтервалі.
, якщо всі точки кривої з цього інтервалу лежать вище будь-якої її дотичної проведеної на цьому інтервалі.
Означення 12.3. Точки кривої, які відділяють опуклу частину від вгнутої, називаються точками перегину кривої.
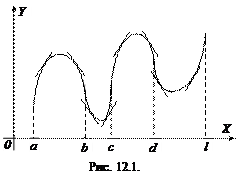
Крива, яка показана на рис. 12.1, є опуклою на інтервалах 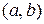 і
і 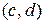 та вгнутою на інтервалах
та вгнутою на інтервалах  і
і 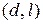 . Точки b, c, d є точками перегину.
. Точки b, c, d є точками перегину.
12.2. Дослідження кривої на опуклість і вгнутість.
Теорема 12.1. Якщо при всіх значеннях х з інтервалу 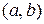 друга похідна функції
друга похідна функції 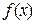 від’ємна, тобто
від’ємна, тобто  , то крива
, то крива  опукла на
опукла на 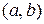 .
.
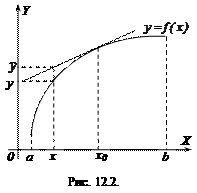
Доведення. Розглянемо криву  (рис. 12.2). В точці
(рис. 12.2). В точці  проведемо дотичну. Потрібно показати, що для будь-якого
проведемо дотичну. Потрібно показати, що для будь-якого  має місце нерівність
має місце нерівність
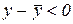 , (12.1)
, (12.1)
де  і
і 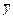 – відповідні ординати графіка функції і дотичної.
– відповідні ординати графіка функції і дотичної.
Крива задається рівнянням  , а дотична – згідно з (9.6)
, а дотична – згідно з (9.6)
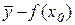
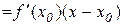
або
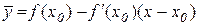 .
.
Тому різниця ординат 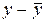 запишеться так:
запишеться так:
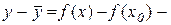
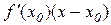 . (12.2)
. (12.2)
З існування другої похідної  на інтервалі
на інтервалі 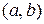 випливає, що функція
випливає, що функція 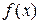 неперервна і диференційована на інтервалі між точками х і х0 , а це означає що до різниці
неперервна і диференційована на інтервалі між точками х і х0 , а це означає що до різниці 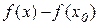 можна застосувати теорему Лагранжа, тобто
можна застосувати теорему Лагранжа, тобто
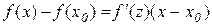 , (12.3)
, (12.3)
де z лежить між точками х і х0 . Підставляючи (12.3) в (12.2), отримаємо
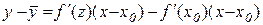
або
 . (12.4)
. (12.4)
Але функція  також неперервна і диференційована на інтервалі
також неперервна і диференційована на інтервалі 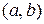 , тому за теоремою Лагранжа маємо
, тому за теоремою Лагранжа маємо
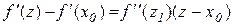 , (12.5)
, (12.5)
де z1 знаходиться між точками z і х0 .
Підставимо (12.5) в (12.4):
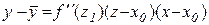
Оскільки 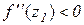 (за умовою) і
(за умовою) і  при
при  та
та 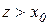 при
при  , то
, то

для всіх х з інтервалу 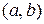 , тобто рівність (12.1) доведено
, тобто рівність (12.1) доведено 
Аналогічно доводиться теорема про вгнутість кривої.
Теорема 12.2. Якщо при всіх значеннях х з інтервалу 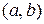 друга похідна функції
друга похідна функції 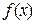 додатна, тобто
додатна, тобто 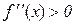 , то крива
, то крива  на цьому інтервалі вгнута
на цьому інтервалі вгнута 
Встановимо достатні умови існування точок перегину.
Означення 12.4. Якщо в точці 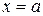 функція
функція 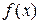 і її перша похідна
і її перша похідна  визначені, а друга похідна
визначені, а друга похідна  рівна нулю або не існує, то дану точку називають критичною точкою першої похідної.
рівна нулю або не існує, то дану точку називають критичною точкою першої похідної.
Теорема 12.3. Нехай функція 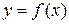 визначена в критичній точці першої похідної
визначена в критичній точці першої похідної 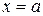 .
.
Якщо друга похідна 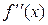 при переході аргументу через точку
при переході аргументу через точку 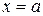 змінює знак, то точка кривої з абсцисою
змінює знак, то точка кривої з абсцисою 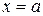 є точкою перегину.
є точкою перегину.
Доведення. 1) Нехай  при
при  , і
, і 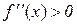 при
при  . Тоді при
. Тоді при  крива є опуклою, а при
крива є опуклою, а при 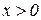 – угнутою. Таким чином, за означенням 12.3 точка з абсцисою
– угнутою. Таким чином, за означенням 12.3 точка з абсцисою 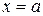 є точкою перегину (рис. 12.3 а).
є точкою перегину (рис. 12.3 а).
2) Якщо 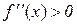 при
при  і
і  при
при 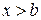 , то за
, то за 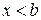 крива є вгнутою, а за
крива є вгнутою, а за 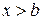 – опуклою. Таким чином, точка з абсцисою
– опуклою. Таким чином, точка з абсцисою  є точкою перегину (рис. 12.3 б)
є точкою перегину (рис. 12.3 б) 
Зауваження 12.1. Опуклість кривої в подальшому позначатимемо значком  , а вгнутість –
, а вгнутість –  .
.
Розглянемо декілька прикладів.
Приклад 12.1. Знайти точки перегину і інтервали опуклості та вгнутості кривої  .
.
Розв’язування. 1) Знаходимо першу й другу похідну:
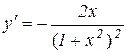 ,
, 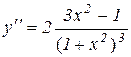 .
.
2) Знаходимо критичні точки першої похідної:
а) точки, де друга похідна рівна нулю:


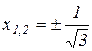 ;
;
 |
б) точок, де друга похідна не існує, немає.
 3) Аналогічно першій похідній (приклад 11.5) знаходимо знаки другої похідної на інтервалах між критичними точками (рис. 12.4).
3) Аналогічно першій похідній (приклад 11.5) знаходимо знаки другої похідної на інтервалах між критичними точками (рис. 12.4).
В точках 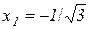 і
і 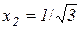 друга похідна змінює свій знак, значить точки з координатами
друга похідна змінює свій знак, значить точки з координатами
 і
і 
є точками перегину.
4) На інтервалах  і
і  друга похідна
друга похідна 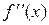 додатна, тому крива
додатна, тому крива  тут вгнута, а на інтервалі
тут вгнута, а на інтервалі 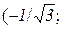
 , де друга похідна від’ємна, крива опукла.
, де друга похідна від’ємна, крива опукла.
Приклад 12.2. Знайти точки перегину і інтервали опуклості і вгнутості кривої 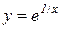 .
.
Розв’язання. 1) Знаходимо область визначення функції
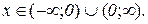 .
.
2) Знаходимо першу й другу похідну:
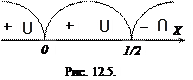
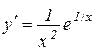 ,
, 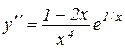 .
.
3) Критичні точки першої похідної:
а) точки, де 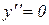 :
:

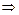
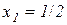 ;
;
б) точки, де  не існує:
не існує:  .
.
4) Відкладаємо критичні точки на числовій прямій і знаходимо знаки другої похідної на інтервалах між критичними точками (рис. 12.5).
 5) Точка з координатами
5) Точка з координатами 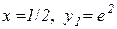 є точкою перегину кривої
є точкою перегину кривої 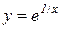 .
.
6) На інтервалах 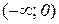 і
і 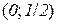 крива вгнута, а на –
крива вгнута, а на –  опукла.
опукла.
12.3. Поняття асимптот та їх види.
Часто, досліджуючи якісну поведінку кривих, потрібно знаходити поведінку кривої при необмеженому зростанні абсциси або ординати. Інколи криві наближаються до певних прямих.
Означення 12.4. Пряма називається асимптотою кривої  , якщо відстань
, якщо відстань 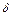 від змінної точки М кривої до даної прямої наближається до нуля при віддалені точки М на нескінченність вздовж кривої.
від змінної точки М кривої до даної прямої наближається до нуля при віддалені точки М на нескінченність вздовж кривої.
Покажемо це на прикладах.
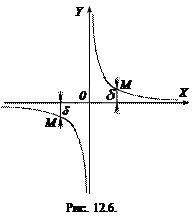
Приклад 12.3. Крива  має дві асимптоти
має дві асимптоти 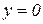 і
і  (рис. 12.6).
(рис. 12.6).
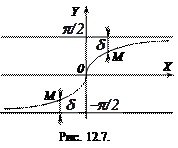
Приклад 4. Крива 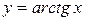 має теж дві асимптоти
має теж дві асимптоти 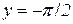 і
і 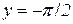 (рис. 12.7).
(рис. 12.7).
Взагалі будемо розрізняти два види асимптот – вертикальні і похилі.
12.4. Вертикальні асимптоти.
Означення 12.5. Вертикальними назвемо асимптоти паралельні осі ординат.
З означення асимптоти випливає, що пряма 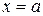 є вертикальною асимптотою тоді, коли виконується хоча б одна з умов
є вертикальною асимптотою тоді, коли виконується хоча б одна з умов
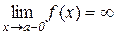 або
або  .
.
Тобто, щоб відшукати вертикальні асимптоти, потрібно знайти такі значення 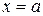 , при наближенні до яких значення функція
, при наближенні до яких значення функція  прямує до нескінченності. Це може відбуватися тільки в яких переривається область визначення функції
прямує до нескінченності. Це може відбуватися тільки в яких переривається область визначення функції 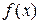 .
.
Приклад 12.5. Крива
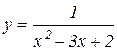
має дві вертикальні асимптоти 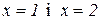 , тому що
, тому що
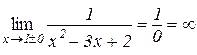 і
і  .
.
Приклад 12.6. Крива 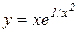 має вертикальну асимптоту
має вертикальну асимптоту  , оскільки за правилом Лопіталя
, оскільки за правилом Лопіталя
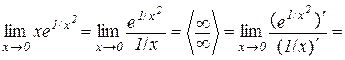
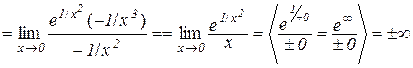 .
.
 |
12.5. Похилі асимптоти.
Рівняння похилої асимптоти згідно з означенням можна записати у вигляді
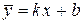 . (12.4)
. (12.4)
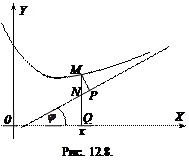 Нехай крива
Нехай крива  має похилу асимптоту (рис. 12.8). Знайдемо значення чисел
має похилу асимптоту (рис. 12.8). Знайдемо значення чисел 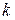 і
і 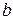 .
.
Якщо 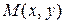 – точка, яка лежить на кривій, а
– точка, яка лежить на кривій, а 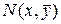 – точка, яка розташована на асимптоті, то з означення асимптоти маємо
– точка, яка розташована на асимптоті, то з означення асимптоти маємо
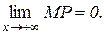 . (12.5)
. (12.5)
Позначимо через 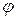 кут нахилу асимптоти до осі
кут нахилу асимптоти до осі  . Тоді з прямокутного трикутника
. Тоді з прямокутного трикутника  отримаємо
отримаємо
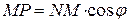 . (12.6)
. (12.6)
Оскільки кут 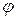 сталий (не рівний
сталий (не рівний 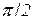 ), то з рівностей (12.5) і (12.6) дістанемо
), то з рівностей (12.5) і (12.6) дістанемо
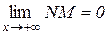 . (12.7)
. (12.7)
Але
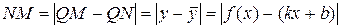 ,
,
тому рівність (12.7) набирає вигляду
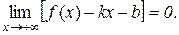 . (12.8)
. (12.8)
Таким чином, якщо пряма (12.4) є асимптотою кривої  , то виконується рівність (12.8), і, навпаки, якщо виконується рівність (12.8), то пряма (12.4) є асимптотою кривої
, то виконується рівність (12.8), і, навпаки, якщо виконується рівність (12.8), то пряма (12.4) є асимптотою кривої  .
.
Знайдемо 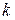 і
і 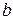 . Для цього в (12.8) винесемо за дужки х:
. Для цього в (12.8) винесемо за дужки х:
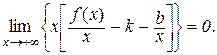 .
.
Так як 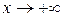 , то повинна виконуватись умова
, то повинна виконуватись умова
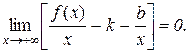 .
.
При сталому b маємо
 .
.
Таким чином,

або
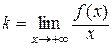 . (12.9)
. (12.9)
Підставивши (12.9) в (12.8) знаходимо b:
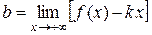 . (12.10)
. (12.10)
Отриманий результат можна сформулювати наступним чином: для того щоб пряма (12.4) була асимптотою кривої  , необхідно і достатньо, щоб існували скінчені границі (12.9) і (12.10).
, необхідно і достатньо, щоб існували скінчені границі (12.9) і (12.10).
Аналогічний результат має місце і для випадку  .
.
Розглянемо кілька прикладів.
Приклад 12.7. Знайти похилі асимптоти графіка функції
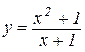 .
.
Розв’язання. Похилі асимптоти мають вигляд  . Шукаємо
. Шукаємо 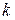 і
і 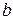 :
:
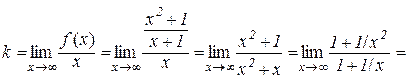
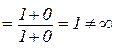 ;
;
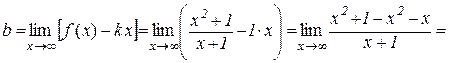
 .
.
Таким чином, пряма 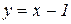 є похилою асимптотою заданої функції.
є похилою асимптотою заданої функції.
Приклад 12.8. Знайти асимптоти лінії 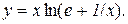 .
.
Розв’язання. 1) Вертикальні асимптоти:
а) область визначення функції:  або
або
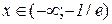
 ;
;
б) з пункту а) випливає, що на існування вертикальних асимптот потрібно перевірити тільки точки 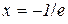 і
і 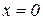 , тобто точки, де переривається область визначення. Зміст мають лівостороння границя функції в точці
, тобто точки, де переривається область визначення. Зміст мають лівостороння границя функції в точці 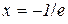 і правостороння границя – в точці
і правостороння границя – в точці 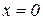 . Знайдемо їх:
. Знайдемо їх:
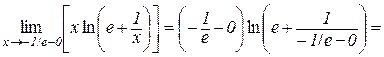
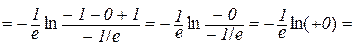
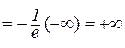 .
.

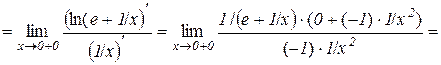
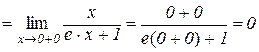 .
.
Таким чином, вертикальною асимптотою даної лінії є пряма 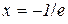 . В точці
. В точці 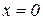 асимптоти немає.
асимптоти немає.
2) Похилі асимптоти. З області визначення слідує, що похилі асимптоти потрібно шукати при 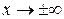 .
.
Знаходимо 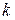 і
і 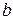 :
:
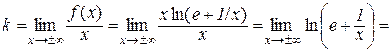
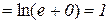 ;
;
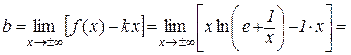
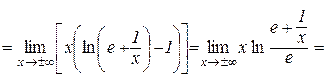
 .
.
Таким чином, пряма  є похилою асимптотою.
є похилою асимптотою.
Приклад 12.9. Знайти асимптоти лінії 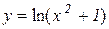 .
.
Розв’язання. 1) Вертикальних асимптот не існує, оскільки областю визначення даної функції є вся числова вісь.
2) Похилі асимптоти шукаємо у вигляді 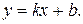 . Знаходимо
. Знаходимо 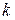 і
і 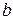 :
:
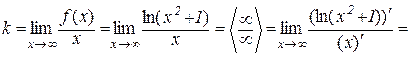
 ;
;
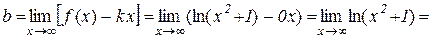
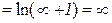 .
.
Таким чином, похилих асимптот також не існує, оскільки b не є скінченим числом.
Запитання для самоконтролю.
1. Дайте означення опуклості і вгнутості та точок перегину кривої.
2. Сформулюйте і доведіть умову опуклості і вгнутості кривої.
3. Яка умова існування точки перегину?
4. Наведіть схему дослідження кривої на опуклість і вгнутість.
5. Дайте означення асимптоти кривої.
6.Виведіть рівняння похилих асимптот.
Приклади до розділу 12.
1. Знайти інтервали вгнутості й опуклості та точки перегину кривих:
а)  . Відп.: Крива всюди опукла.
. Відп.: Крива всюди опукла.
б) 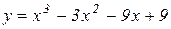 . Відп.: (1;-2) точка перегину.
. Відп.: (1;-2) точка перегину.
в)  . Відп.: (2;2е–2) точка перегину.
. Відп.: (2;2е–2) точка перегину.
г)  . Відп.:
. Відп.: 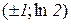 точки перегину.
точки перегину.
2. Знайти асимптоти кривих:
а) 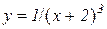 . Відп.:
. Відп.: 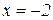 ,
,  .
.
б)  . Відп.:
. Відп.: 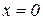 ,
, 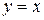 .
.
в) 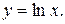 . Відп.:
. Відп.:  .
.
г) 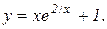 . Відп.:
. Відп.: 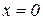 ,
, 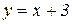 .
.
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 853; Нарушение авторских прав?; Мы поможем в написании вашей работы!