Временные ряды

3.

2.

1.

Теоретическая линейная модель множественной регрессии имеет вид:

(1)

соответствующую выборочную регрессию обозначим:

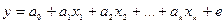(2)

Как и в парной регрессии случайный член ε должен удовлетворять основным предположениям регрессионного анализа. Тогда с помощью МНК получают наилучшие несмещенные и эффективные оценки параметров теоретической регрессии. Кроме того переменные Х₁,Х₂,…,Х_k должны быть некоррелированы (линейно независимы) друг с другом. Для того, чтобы записать формулы для оценки коэффициентов регрессии (2), полученные на основе МНК, введем следующие обозначения:

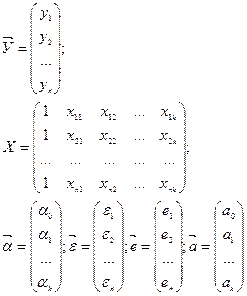
Тогда можно записать в векторно-матричной форме теоретическую модель:

и выборочную регрессию

.

МНК приводит к следующей формуле для оценки вектора коэффициентов выборочной регрессии:

(3)

Для оценки коэффициентов множественной линейной регрессии с двумя независимыми переменными , можно решить систему уравнений:

(4)

Как и в парной линейной регрессии для множественной регрессии рассчитывается стандартная ошибка регрессии S:

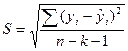(5)

и стандартные ошибки коэффициентов регрессии:

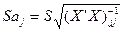(6)

значимость коэффициентов проверяется с помощью t-критерия.

(7)

имеющего распространение Стьюдента с числом степеней свободы v= n-k-1.

Для оценки качества регрессии используется коэффициент (индекс) детерминации:

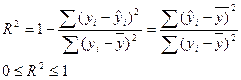, (8)

чем ближе к 1, тем выше качество регрессии.

Для проверки значимости коэффициента детерминации используется критерий Фишера или F- статистика.

(9)

с v₁ =k, v₂ =n-k-1 степенями свободы.

В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Для компенсации такого увеличения вводится скорректированный (или нормированный) коэффициент детерминации:

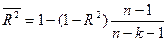(10)

Если увеличение доли объясняемой регрессии при добавлении новой переменной мало, то 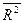может уменьшиться. Значит, добавлять новую переменную нецелесообразно.

Пример 4:

Пусть рассматривается зависимость прибыли предприятия от затрат на новое оборудование и технику и от затрат на повышение квалификации работников. Собраны статистические данные по 6 однотипным предприятиям. Данные в млн. ден. ед. приводятся в таблице 1.

Таблица 1

Номер предприятия, i	Прибыль i-го предприятия, уi	Затраты на новое оборудование i-го предприятия, хi1	Затраты на повышение квалификации на i-м предприятии, хi2

Построить двухфакторную линейную регрессию и оценить ее значимость. Введем обозначения:

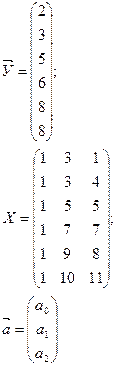
Транспонируем матрицу Х:

Обращение этой матрицы:

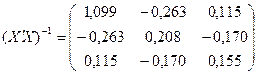
таким образом зависимость прибыли от затрат на новое оборудование и технику и от затрат на повышение квалификации работников можно описать следующей регрессией:

Используя формулу (5), где k=2 рассчитаем стандартную ошибку регрессии S=0,636.

Стандартные ошибки коэффициентов регрессии рассчитаем, используя формулу (6):

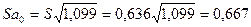
Аналогично:

Проверим значимость коэффициентов регрессии а₁, а₂. посчитаем t_расч.

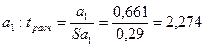
Выберем уровень значимости 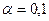, число степеней свободы

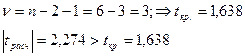
значит коэффициент а₁ значим.

Оценим значимость коэффициента а₂:

Коэффициент а₂ незначим.

Рассчитаем коэффициент детерминации по формуле (7) 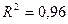. Прибыль предприятия на 96% зависит от затрат на новое оборудование и технику и повышение квалификации на 4% от прочих и случайных факторов. Проверим значимость коэффициента детерминации. Рассчитаем F_расч.:

т.о. коэффициент детерминации значим, уравнение регрессии значимо.

Большое значение в анализе на основе многофакторной регрессии имеет сравнение влияния факторов на зависимый показатель у. Коэффициенты регрессии для этой цели не используется, из-за различий единиц измерения и различной степени колеблемости. От этих недостатков свободные коэффициенты эластичности:

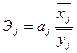(11)

Эластичность показывает, на сколько процентов в среднем изменяется зависимый показатель у при изменении переменной на 1% при условии неизменности значений остальных переменных. Чем больше 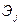, тем больше влияние соответствующей переменной. Как и в парной регрессии для множественной регрессии различают точечный прогноз и интервальный прогноз. Точечный прогноз (число) получают при подстановке прогнозных значений независимых переменных в уравнение множественной регрессии. Обозначим через:

(12)

вектор прогнозных значений независимых переменных, тогда точечный прогноз

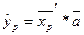(13)

или

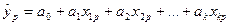(14)

Стандартная ошибка предсказания в случае множественной регрессии определяется следующим образом:

(15)

Выберем уровень значимости α по таблице распределения Стьюдента. Для уровня значимости α и числа степеней свободы ν = n-k-1 найдем t_кр. Тогда истинное значение у_р с вероятностью 1- α попадает в интервал:

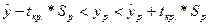(16)

Тема 5:

Вопросы:

1. Основные понятия временных рядов.

2. Основная тенденция развития – тренд.

3. Построение аддитивной модели.

Дата добавления: 2014-11-18