Формула полной вероятности. Формула Байеса

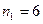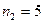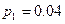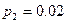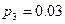24. В ящике содержатся деталей, изготовленных на заводе 1, деталей – на заводе 2 и деталей – заводе 3. Вероятности изготовления брака на заводах с номерами 1, 2 и 3 соответственно равны , и . Найдите вероятность того, что извлеченная наудачу деталь окажется качественной.

Hi- гипотеза, что деталь изготовлена на i заводе

P(Hi)-вероятность того, что деталь изготовлена на 1 заводе

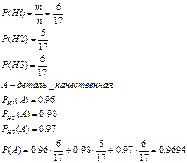
25. В урну, содержащую 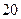шаров, опущен белый шар, после чего наудачу извлечен один шар. Найдите вероятность того, что извлеченный шар окажется белым, если равновероятны все возможные предположения о первоначальном количестве белых шаров в урне.

Hi-первоначально в урне i белых шаров

i=0,….20

А- событие, сост, в том, что извлечен белый шар

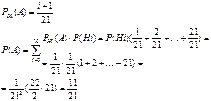
26. В первой урне 5 белых и 3 черных шара, во второй – 6 белых и 9 черных. Из второй урны случайным образом перекладывают в первую два шара, после чего из первой урны берут один шар. Какова вероятность того, что этот шар – белый?

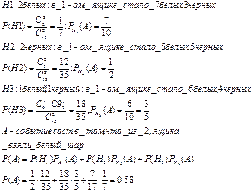
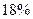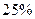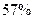27. С первого станка-автомата на сборочный конвейер поступает деталей, со 2-го и 3-го – по и соответственно. Вероятности выдачи бракованных деталей составляют для каждого из них соответственно 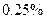, 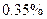и 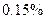. Найдите вероятность того, что поступившая на сборку деталь окажется бракованной, а также вероятности того, что она изготовлена на 1-м, 2-м и 3-м станках-автоматах, при условии, что она оказалась бракованной.

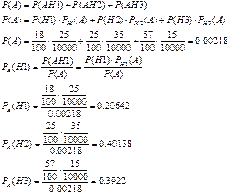
28. Имеется три одинаковых по виду ящика. В первом ящике 23 белых шара, во втором – 9 белых и 14 черных шаров, в третьем – 23 черных шара. Из выбранного наугад ящика вынули белый шар. Найдите вероятность того, что шар вынут из второго ящика.

	1 ящик	2 ящик	3 ящик
Кол-во шаров	23	23	23
% шаров ко всем	1/3	1/3	1/3
Кол-во белых шаров	23	9	0
% белых шаров к ящику	1	9/23	0

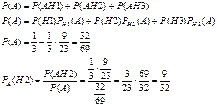
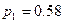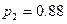29. В среднем из 100 клиентов банка 53 обслуживаются первым операционистом и 47 – вторым. Вероятности того, что клиент будет обслужен без помощи заведующего отделением, только самим операционистом, составляет и соответственно для первого и второго служащих банка. Какова вероятность, что клиент, для обслуживания которого потребовалась помощь заведующего, был направлен к первому операционисту?

n1-1-ый операционист

n2-2-ой операционист

А-событие, сост. в том, что, что потребуется помощь заведующего

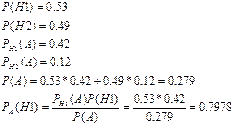
30. Имеется 13 монет, из которых 3 штуки бракованные: вследствие заводского брака на этих монетах с обеих сторон отчеканен герб. Наугад выбранную монету, не разглядывая, бросают 9 раз, причем при всех бросаниях она ложится гербом вверх. Найдите вероятность того, что была выбрана монета с двумя гербами.

H1-монета хорошая

H2 – бракованная монета

А-событие, состю в том, что при всех бросании монета легла гербом

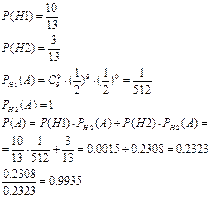
31. Детали, изготовленные в цехе, попадают к одному из 2-х контролёров. Вероятность того, что деталь попадёт к 1-му контролёру, равна 0,8; ко 2-му – 0,2. Вероятность того, что годная деталь будет признана стандартной 1-м контролёром равна 0,96; 2-м контролёром – 0,98. Годная деталь при проверке оказалась стандартной. Найдите вероятность того, что эту деталь проверял 1-й контролёр.

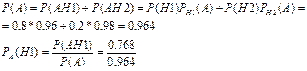
32. Пассажир может обратиться за получением билета в одну из трёх касс (А,B,C). Вероятности обращения в каждую кассу зависят от их местонахождения и равны соответственно 0,4;0,5 и 0,1. Вероятности того, что к моменту прихода пассажира, имеющиеся в кассе билеты распроданы равны соответственно 0,4; 0,3 и 0,1. Найдите вероятность того, что билет куплен. В какой из касс это могло произойти с наибольшей вероятностью?

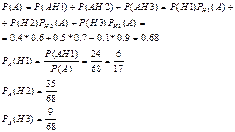
33. В первой урне 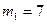белых и 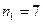черных шаров, во второй – 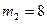белых и 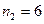черных. Из второй урны случайным образом перекладывают в первую два шара, после чего из первой урны берут один шар, который оказывается белым. Какова вероятность того, что два шара, переложенные из второй урны в первую, были разных цветов?

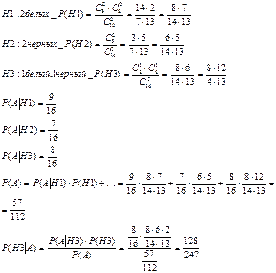
● Схема Бернулли. Числа 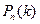. Наиболее вероятное число успехов

34. Вероятность попадания в цель при одном выстреле равна 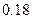. Сделано 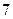выстрелов. Найдите вероятность того, что в цель попали менее трех раз.

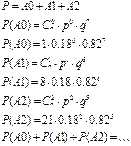
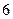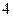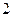35. Отрезок длины поделен на две части длины и соответственно, 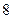точек последовательно бросают случайным образом на этот отрезок. Найдите вероятность того, что количество точек, попавших на отрезок длины 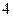будет больше или меньше .

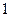М-событие, сост. в том, что на отрезок АС попало не менее 2 точек

М с чертой – событие, сост. в том, что попало 2 точки

Р – вероятность попадания на АС при 1 бросании

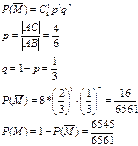
36. Вероятность попадания стрелком в цель равна 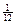. Сделано выстрелов. Определите наивероятнейшее число попаданий в цель.

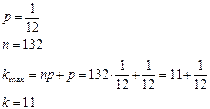
● Схема Бернулли. Приближенные формулы Лапласа и Пуассона

37. Вероятность выпуска бракованного изделия равна 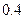. Найдите вероятность того, что среди 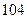выпущенных изделий ровно 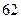изделий без брака.

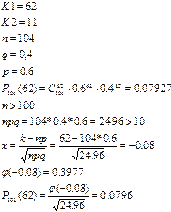
38. Вероятность выпуска бракованного изделия равна 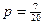. Найдите вероятность того, что среди 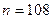выпущенных изделий будет хотя бы одно, но не более 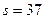бракованных изделий.

39. Всхожесть семян данного растения равна 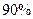. Найдите вероятность того, что из 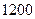посаженных семян число проросших семян заключено между и .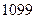

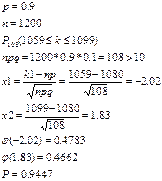
40. Прядильщица обслуживает 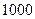веретен. Вероятность обрыва нити на одном веретене в течение 1 минуты равна . Найдите вероятность того, что в течение одной минуты обрыв произойдет более чем на 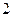веретенах.

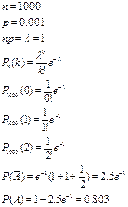
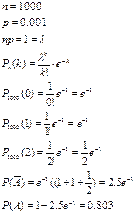
41. Завод отправил на базу 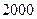доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна . Какова вероятность того, что на базу поступят 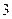некачественных изделия?

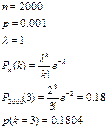
42. При введении вакцины против полиомиелита иммунитет создается в 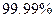случаях. Определите вероятность того, что из 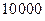вакцинированных детей заболеют .

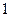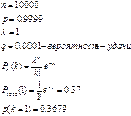
Дата добавления: 2014-11-08