Лекция №3. Измерение количества информации

Объемный подход

Измерение количества информации

Работы Джон фон Неймана по созданию ЭВМ привели к объемному подходу измерения количества информации.

Объем информации в сообщении – это количество символов в сообщении. Поскольку, например, одно и то же число может быть записано многими разными способами (использованием разных алфавитов):

«двадцать пять»

XXV

то этот способ чувствителен форме представления (записи) сообщения. В вычислительной технике вся обрабатываемая и хранимая информация вне зависимости от ее природы (число, текст, отображение) представлена в двоичной форме с использованием алфавита, состоящего из двух символов 0 и 1, называемых битами (от английского Binary digit — двоичная цифра). Такая стандартизация позволила ввести две стандартные единицы: бит и байт. Байт – это восемь бит.

Для измерения количества информации используются также более крупные единицы:

1 Килобайт = 1024 байта (2¹⁰ байта)

1 Мегабайт =1024 Кбайта (2²⁰ байта)

1 Гигабайт = 1024 Мбайта (2³⁰ байта)

1 Терабайт = 1024 Гбайта (2⁴⁰ байта)

1 Петабайт = 1024 Тбайта (2⁵⁰ байта)

1 Экзабайт = 1024 Пбайта (2⁶⁰ байта)

Контрольные вопросы

1. Как Вы понимаете понятие информации и какое определение можно дать?

2. Какие существуют подходы к определению количества информации и кто их открыл?

3. Чем отличается байт от бита?

4. Более крупные единицы измерения информации и как они определяются?

5. Сколько различных информации можно написать одним байтом и обоснуйте почему?

6. В чем состоит процедура дискретизации непрерывной информации?

7. Какая форма представления информации - непрерывная или дискретная приемлема для компьютеров и почему?

Литература: Основная [1,2,3, 4], дополнительная [1-4]

Тема: Системы счисления. Методы перевода чисел из одной системы счисления в другую.

Цель: Ознакомить с позиционными системами счисления, используемыми при работе на компьютере. Показать способы перевода из одной позиционной системы счисления в другую.

Ключевые понятия: Система счисления, позиционные системы счисления, непозиционные системы счисления, двоичная арифметика.

Система счисления - принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса: позиционные и непозиционные. Для записи чисел в различных системах счисления используется некоторое количество отличных друг от друга знаков. Число таких знаков в позиционной системе счисления называется основанием системы счисления. В позиционной системе счисления число может быть представлено в виде суммы произведений коэффициентов на степени основания системы счисления:

A_nA_n-1A_n-2 … A₁,A₀,A_-1,A_-2 =

А_nВⁿ + A_n-1B^n-1 +... + A₁B¹ + А₀В⁰ + A_-1B^-1 + А_-2В^-2 +...

(знак «точка» отделяет целую часть числа от дробной; знак «звездочка» здесь и ниже используется для обозначения операции умножения). Таким образом, значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа. Именно поэтому такие системы счисления называют позиционными.

23,43(₁₀) = 2*10¹ + З*10° + 4*10^-1 + З*10^-2

692(₁₀) = 6* 10² + 9*10¹ + 2.

1101(₂)= 1*2³ + 1*2²+0*2¹+ 1*2°;

112(₃) = l*3²+ 1*3¹ +2*3°;

341,5(₈) =3*8²+ 4*8¹ +1*8° +5*8^-1;

A1F4(₁₆) = A*16² + 1*16¹ + F*16° + 4*16^-1.

При работе с компьютерами приходится параллельно использовать несколько позиционных систем счисления (чаще всего двоичную, десятичную и шестнадцатиричную), поэтому большое практическое значение имеют процедуры перевода чисел из одной системы счисления в другую.Заметим, что во всех приведенных выше примерах результат является десятичным числом, и, таким образом, способ перевода чисел из любой позиционной системы счисления в десятичную уже продемонстрирован.

А чтобы перевести целую часть числа из десятичной системы в систему с основанием В, необходимо разделить ее на В. Остаток даст младший разряд числа. Полученное при этом частное необходимо вновь разделить на В - остаток даст следующий разряд числа и т.д. Для перевода дробной части ее необходимо умножить на В. Целая часть полученного произведения будет первым (после запятой, отделяющей целую часть от дробной) знаком. Дробную же часть произведения необходимо вновь умножить на В. Целая часть полученного числа будет следующим знаком и т.д. Процесс умножения продолжается до тех пор, пока дробные части не обратятся в нуль или не обнаружится период, или пока не будет достигнута точность представления по точности исходной дроби.

Например, пусть требуется перевести число 1982 в семиричную систему. Выпишем остатки в обратном порядке и получим: 5531₍₇₎== 1982.

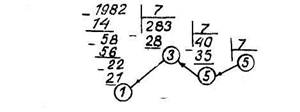
Переведем издесятичной системы в двоичную дробь 0,6875.

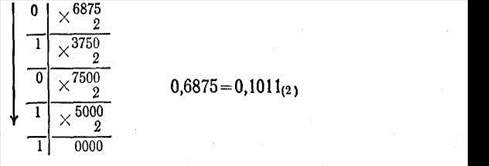
Пусть требуется перевести 0,52 в семиричную систему счисления.

В этом примере мы видим, что 0,52 в 7-с/с имеет период (3432), поэтому процесс прекращен после получения той же дроби 0,52. 0,52 = 0,(3432) Кроме рассмотренных выше позиционных систем счисления существуют такие, в которых значение знака не зависит от того места, которое он занимает в числе. Такие системы счисления называются непозиционными. Наиболее известным примером непозиционной системы является римская. В этой системе используется 7 знаков (I, V, X, L, С, D, М), которые соответствуют следующим величинам:

1(1) V(5) X(10) L(50) С (100) D(500) M(1000)

Примеры: III (три), LIX (пятьдесят девять), DLV (пятьсот пятьдесят пять).

Недостатком непозиционных систем, из-за которых они представляют лишь исторический интерес, является отсутствие формальных правил записи чисел и, соответственно, арифметических действий над ними (хотя по традиции римскими числами часто пользуются при нумерации глав в книгах, веков в истории и др.).

Двоичная система. Двоичная арифметика.

Двоичная система является основой представления данных, выполнения операций и организации работы компьютера. Фактически алфавит компьютера состоит из двоичного базиса, наиболее простого устройства с двумя устойчивыми состояниями.

Таблица 1 Таблица 2 Таблица 3

(сложения) (вычитания) (умножения)

0 + 0= 0 0-0=0 0*0 = 0

0+1=1 1-0=1 0*1=0

1 + 0 = 1 1-1 = 0 1*0 = 0

1 + 1 = 10 10-1 = 1 1*1=1

Примеры арифметических операций в двоичной системе. Вычислим в двоичной системе

Приведенный выше пример показывает, что двоичная система очень удобна для вычислений; операция умножения сводится к простому сложению со сдвигом множителя по позиции, а деление — к вычитанию, причем сложение (вычитание) производятся только один раз на разряд множителя (частного). Однако неудобной является запись чисел, которая однообразна и громоздка; легко допустить описку. Для записи двоичных кодов широко используется шестнадцатиричный код.

Дата добавления: 2014-11-20