Система обозначений в анализе алгоритмов

При более детальном анализе трудоемкости алгоритма оказывается, что не всегда количество элементарных операций, выполняемых алгоритмом на одном входе длины N, совпадает с количеством операций на другом входе такой же длины. Это приводит к необходимости введения специальных обозначений, отражающих поведение функции трудоемкости данного алгоритма на входных данных фиксированной длины.

Пусть D _А — множество конкретных проблем данной задачи, заданное в формальной системе. Пусть D_Ғ, D _А — задание конкретной проблемы и |D|=N.

В общем случае существует собственное подмножество множества D _А, включающее все конкретные проблемы, имеющие мощность N:

- обозначим это подмножество через D_N:D _N= {D_Ғ, D_N: |D| = N};

- обозначим мощность множества D_N через M_DN → M_DN=|D_N |.

Тогда содержательно данный алгоритм, решая различные задачи размерности N, будет выполнять в каком-то случае наибольшее количество операций, а в каком-то случае наименьшее количество операций. Введем следующие обозначения:

1. F _α ^(N) - худший случай - наибольшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:

F _α ^(N) = max { F _α (D)}

DD_N -худший случай на D_N.

2. F _α 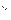(N) - лучший случай - наименьшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:

F_a 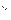(N) = min {F_a (D)}

DD_N - лучший случай на D_N

3. 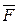_α(N) - средний случай - среднее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:

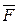_a(N)=(1/M_DN}·Σ{F_a(D)}

DÎD_N - средний случай на D_N

3. Классификация алгоритмов по виду функции трудоёмкости

В зависимости от влияния исходных данных на функцию трудоемкости алгоритма может быть предложена следующая классификация, имеющая практическое значение для анализа алгоритмов:

1. Количественно-зависимые по трудоемкости алгоритмы

Это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений:

F_a(D) = F_a (|D|)= F_a(N)

Примерами алгоритмов с количественно-зависимой функцией трудоемкости могут служить алгоритмы для стандартных операций с массивами и матрицами - умножение матриц, умножение матрицы на вектор и т.д.

2.Параметрически-зависимые по трудоемкости алгоритмы

Это алгоритмы, трудоемкость которых определяется не размерностью входа (как правило, для этой группы размерность входа обычно фиксирована), а конкретными значениями обрабатываемых слов памяти:

F_a(D) = F_a(d₁,..,d_n) = F_a(P₁,..,P_m),m=<n

Примерами алгоритмов с параметрически-зависимой трудоемкостью являются алгоритмы вычисления стандартных функций с заданной точностью путем вычисления соответствующих степенных рядов. Очевидно, что такие алгоритмы, имея на входе два числовых значения - аргумент функции и точность выполняют существенно зависящее от значений количество операций.

а) Вычисление x^kпоследовательным умножением Þ F_a(x,k) = F_a(k).

б) Вычисление e ^x=Σ(x^-n/n!), с точностью до ξ => F_a= F_a(х,ξ)

3. Количественно-параметрические по трудоемкости алгоритмы

Однако в большинстве практических случаев функция трудоемкости зависит как от количества данных на входе, так и от значений входных данных, в этом случае:

F_a(D) = F_a(||D||,P₁,..,P_m)=F_a(N,P₁,..,P_m)

В качестве примера можно привести алгоритмы численных методов, в которых параметрически-зависимый внешний цикл по точности включает в себя количественно-зависимый фрагмент по размерности.

3.1 Порядково-зависимые по трудоемкости алгоритмы

Среди разнообразия параметрически-зависимых алгоритмов выделим еще оду группу, для которой количество операций зависит от порядка расположения исходных объектов.

Пусть множество D состоит из элементов (d₁,...,d_n), и ||D||=N,

Определим D_p = {(d₁,...,d_n)}-множество всех упорядоченных N-ок из d₁,...,d_n, отметим, что |D_p|=n!.

Если F_a(_iD_p)≠F_a(_jD_p), где _iD_p, _jD_p, _ғD_p, то алгоритм будем называть порядково-зависимым по трудоемкости.

Примерами таких алгоритмов могут служить ряд алгоритмов сортировки, алгоритмы поиска минимума и максимума в массиве. Рассмотрим более подробно алгоритм поиска максимума в массиве S, содержащим n элементов:

MaxS(S,n; Мах)

Max← S₁

For i←2 to n

If Max <S_i

Then Max←S_i

(количество выполненных операций присваивания зависит от порядка следования элементов массива)

Дата добавления: 2014-11-20