Структура сетей электросвязи

Понятие структуры сети раскрывает схему связей и взаимодей­ствия ее элементов. При рассмотрении структуры сети выделяют следующие аспекты её описания: физический, определяющий состав и связи элементов и логический, отображающий взаимодей­ствие элементов в процессе функционирования сети.

Физическая структура сети - это схема связей физических элементов сети: узлов коммутации (УК), оконечных пунктов (ОП) -станций и линий передачи в их взаимном расположении с характе­ристиками передачи и распределения сообщений.

Логическая структура сети определяет принципы установле­ния связей, алгоритмы организации процессов и управления ими, логику функционирования программных средств.

Топологическая структура сети или просто топология - это обобщенная геометрическая модель физической структуры сети.

Более конкретный состав аппаратно-программных средств и схема их связей называется конфигурацией сети.

В дальнейшем, если не оговорено особо, под термином «струк­тура» понимается топологическая структура.

Под архитектурой сети понимается совокупность физической, логической и функциональной структуры.

Основные топологии телекоммуникационных сетей. Выбор конкретной топологии сети влияет не только на ее физическую струк­туру, но и существенно определяет все основные показатели сети.

В одних случаях топология задается заранее, в других - опреде­ляется на разных стадиях проектирования. Разработанная или выбранная топология сети оценивается по различным критериям: надежности, экономичности и т. д. Рассмотрим разновидности топологических структур, получивших наибольшее распространение в телекоммуникационных сетях.

1. Древовидная топология предполагает между каждой парой
узлов только один путь, т.е. связность сети h = 1. На рис. 4.1 показаны
разновидности древовидной топологии.

2. Сетевидная топология, в которой каждый узел является
смежным только с небольшим числом других узлов. Связность
такой сети h > 1. На рис. 5 изображены представители сетевидной
топологии.

3. Полносвязная топология, в которой узлы соединены по принципу «каждый с каждым». На рис. 6 изображена подобная топология.

Если N- число узлов, то число ребер равно 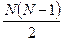ранг узла r = N-1. Без нарушения связности можно исключить N-2 ребер.

Топология сети оказывает значительное влияние на основные показатели сети, особенно на надежность и живучесть. Чем выше связность сети, тем она более живуча и надежна. Наибольшей связностью обладает полносвязная сеть, но для ее реализации требуется максимальное число каналов и, следовательно, сеть имеет высокую стоимость.

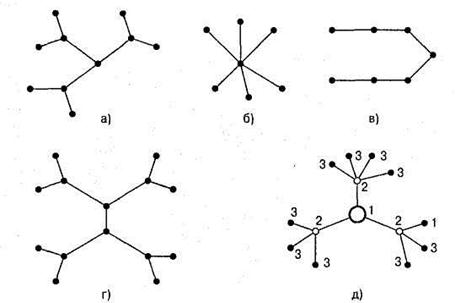
Рис. 13.1 Разновидности древовидной топологии: а -дерево; б -звезда; в -линейная (шина); г -снежинка; д -узловая с иерархией узлов

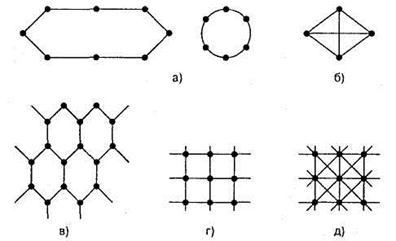
Рис. 13.2. Разновидности сетевидной топологии: а - петлевая (кольцевая); б - радиально-петлевая; в - сотовая; г - решетка; д - двойная решетка

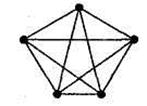
Рис. 13.3 Полносвязная топология

Топология реальной сети обычно строится по иерархическому принципу: крупные узлы соединяются по принципу «каждый с каж­дым», а на низших уровнях используются простые топологии -дерево, шина, звезда, кольцо и т. д.

Дата добавления: 2014-11-08