Свойства дисперсии

1. Если из всех значений вариант вычесть какое-то постоянное число, то средний квадрат отклонений не изменится:

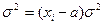
2. Если все значения вариант разделить на какое-то постоянное число, то средний квадрат отклонений уменьшиться в а раз:

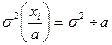
3. Если средний квадрат отклонений от любой величины а – которая отличается от средней арифметической х, то он будет всегда больше среднего квадрата отклонений от средней арифметической: 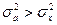, но больше на определенную величину, а эта величина определена, как квадрат разности между средней и этой, условно взятой величиной:

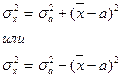
используя 2-ое свойство дисперсии в математической статистике можно рассчитать дисперсию способом моментов. Средний квадрат отклонений от средней величины имеет свойства min, т.е. дисперсия от средней всегда меньше дисперсий исчисляемых от других величин. В этом случае, если а – постоянное число = 0, то, следовательно, средний квадрат отклонений будет определяться по формуле:

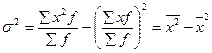
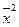- ср. квадрат значений признака;

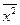- квадрат среднего значения признака.

Значит, средний квадрат отклонений 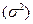равен разности между средним квадратом значения признака и квадратом ср. значения признака.

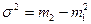
Также способ моментов называется способом отсчета от условного нуля. Данный способ можно применять только в тех случаях, если в вариационных интервальных рядах интервалы одинаковы.

Используя 2-ое свойство дисперсии, разделив все варианты на величину интервала, получим формулу дисперсии:

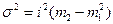
где i – величина интервала для данной совокупности ;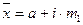

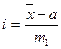
Пример.

Рассчитать все показатели вариации, доказать закон сложения дисперсии.

Общий объем ТП	Число предприятий	Расчет общей дисперсии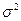
Государст- венных	АО	Всего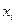
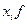
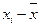
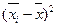
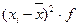
10-12						-7,14	50,9796	152,9388
12-14						-5,14	26,4196	105,6784
14-16						-3,14	9,8596	167,6132
16-18						-1,14	1,2996	33,7896
18-20						0,86	0,7396	14,0524
20-22						2,86	8,1796	188,1308
22-24						4,86	23,6196	141,7176
24-26						6,86	47,0596	94,1192
Итого:								898,04

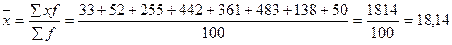
Общая дисперсия

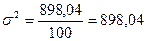
В среднем по региону средний объем товарной продукции равен 18,14 млрд. руб.

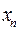
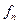
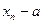
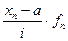
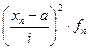
					По АО (где а = 17)
		-6	-9
		-4	-8
		-2	-17
Итого:

,

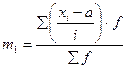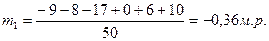
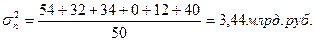
Ср. квадратное отклонение АО: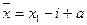

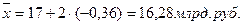по региону средний объем товарной продукции в регионе АО 16,82

,

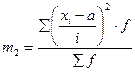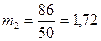
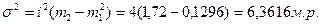
Расчет межгрупповой дисперсии

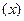
Предприятия по форме собственности	Ср. размер ТП 1 предприятия	Число предприятий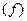
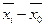
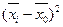
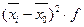
Государственные			1,86	3,4596	172,98
АО	16,28		-1,86	3,4596	172,98

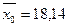
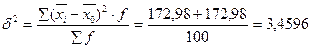
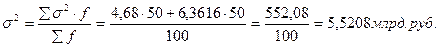
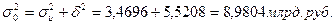Закон сложения дисперсии доказан.

Если разделить дисперсию групповых средних на общую дисперсию, то получим коэффициентдетерминации.

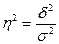
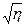- дает эмпирическое корреляционное отношение, показывает тесноту между группировочным признаком и результативным.

Дата добавления: 2014-11-20