
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
З'єднання
|
|
|
|
Приклад
Приклад
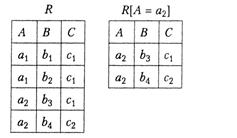
Декартїв добуток
Декартовим добутком реляційних відношень R і S зі схемами R(A1, A2, …, An) та S(B1, B2, …, Вn) відповідно, що позначається R x S, називається відношення  зі схемою
зі схемою  (A1, А2, …,Аn,В1 В2, …, Вn), яке містить усі можливі з'єднання кортежів відношення R з кортежами відношення S:
(A1, А2, …,Аn,В1 В2, …, Вn), яке містить усі можливі з'єднання кортежів відношення R з кортежами відношення S:
 =RxS = {(r,s) | r
=RxS = {(r,s) | r  R&s
R&s  S}.
S}.
Операція комутативна й асоціативна.
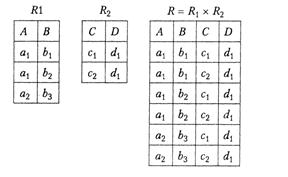
Припустимо, що відношення R має схему R(L, M), а відношення S - схему S(N, P). Нехай множини атрибутів M і N - 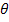 -порівнянні. Тоді з'єднанням, або
-порівнянні. Тоді з'єднанням, або 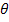 -з'ед нанням, відношень R і S за умовою M
-з'ед нанням, відношень R і S за умовою M 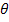 N, що позначається як R[M
N, що позначається як R[M 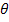 N]S, називається відношення
N]S, називається відношення 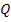 зі схемою
зі схемою 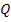 (L, M, N, P), кортежі якого можна отримати з'єднанням тих кортежів відношень R і S, на яких виконується умова M
(L, M, N, P), кортежі якого можна отримати з'єднанням тих кортежів відношень R і S, на яких виконується умова M 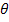 N:
N:
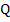 = R[M
= R[M 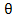 N]S={(r, s) | r
N]S={(r, s) | r 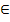 R & s
R & s 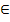 S & r[M]
S & r[M]  s[N]}.
s[N]}.
Під час з'єднання атрибути, за якими виконується така операція, повторюються в кінцевому реляційному відношенні. Операція комутативна й асоціативна.
Іноді операція з'єднання позначається як 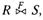 ,де F — умова з'єднання.
,де F — умова з'єднання.
З'єднання за умовою рівності називається еквіз'єднанням. З'єднання за умовою рівності, коли один з порівнюваних атрибутів (чи група порівнюваних атрибутів) видаляється з кінцевого відношення, називається природним з'єднанням; на його позначення використовується символ «*». Наприклад, якщо задані відношення R(A, В, C, D) і S(C, D E ), то в результаті виконання операції Q=R * S отримаємо реляційне відношення 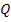 (A, В, C, D, E).
(A, В, C, D, E).
Серед операцій 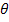 -з'єднання виділяють операцію напівз'єднання, за якої з результату видаляються всі атрибути одного з відношень, що з'єднуються. Вона записується як R[M
-з'єднання виділяють операцію напівз'єднання, за якої з результату видаляються всі атрибути одного з відношень, що з'єднуються. Вона записується як R[M 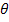 N)S і формально визначається так:
N)S і формально визначається так:
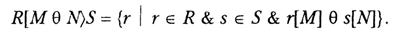
Операція напівз'єднання не розширює можливостей реляційної алгебри, оскільки вона виражається через з'єднання і проекцію в такий спосіб:

|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 344; Нарушение авторских прав?; Мы поможем в написании вашей работы!