Расчет коэффициента корреляции

Исследование статистических взаимосвязей между изучаемыми процессами осуществляется методами корреляционного и регрессионного анализа. Определить направленность и рассчитать силу статистической взаимосвязи признаков можно с помощью коэффициента корреляции, построить математическую модель - с помощью линейной регрессии.

Количественно направленность и сила статистической взаимосвязи (коэффициент корреляции) между признаками X и Y находится по формуле:

(3.9),

где (3.10)

(3.11)

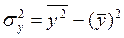(3.12)

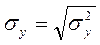(3.13)

Пример. Определить коэффициент корреляции двумя способами: расчетным и с помощью пакета анализа данных.

Рассмотрим реализацию этапов статистического анализа в Excel.

Известно, что наиболее емким показателем уровня жизни населения является «Среднедушевые денежные доходы населения, руб.», а уровень экономического развития территории во много определяется инвестициями. Проверим гипотезу о наличии статистической взаимосвязи между показателями уровня жизни населения и уровня экономического развития территории методом корреляционного анализа. Для этого рассчитаем линейный коэффициент корреляции Пирсона.

Определение линейного коэффициента корреляции расчетным методом наглядно отображено в таблице на рис. 43 (режим формул).

Рис. 43. Фрагмент таблицы в режиме формул расчета линейного коэффициента корреляции

В режиме значений таблица расчета линейного коэффициента корреляции представлена на рис. 44.

Рис. 44. Фрагмент таблицы в режиме значений расчета линейного коэффициента корреляции

Подтвердить значение полученного коэффициента корреляции можно с помощью пакета анализа данных.

Последовательность действий в этом случае следующая:

1. Подготовить исходные данные (рис. 45).

2. Команда СЕРВИЗ – АНАЛИЗ ДАННЫХ.

3. Инструменты анализа – Корреляция.

4. Ввод параметров окна (рис. 46).

5. ОК.

Рис. 45. Фрагмент базы данных.

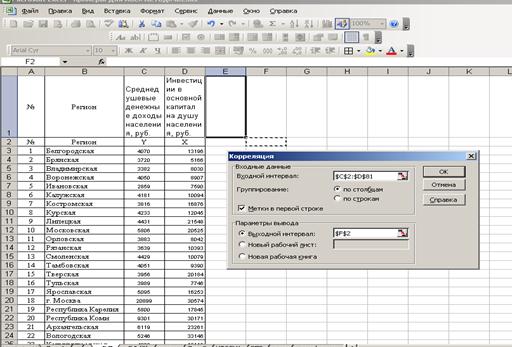
Рис. 46. Ввод параметров окна при определении коэффициента корреляции.

В результате получаем аналогичное значение коэффициента корреляции (r_xy), равное 0,64, что позволяет утверждать о правильности расчета и наличии высокой статистической взаимосвязи между уровнем жизни населения и уровнем экономического развития субъектов Российской Федерации.

Дата добавления: 2014-11-20