Принципы аппроксимации

Цифровые измерительные генераторы низких частот

Цифровые генераторы низких частот по сравнению с аналоговыми характеризуются более эффективными метрологическими характеристиками: высокими точностью установки и стабильностью частоты, малым коэффициентом нелинейных искажений (строго синусоидальной формой), постоянством уровня выходного сигнала. Цифровые генераторы, получающие все более широкое распространение, удобнее аналоговых в эксплуатации: выше быстродействие, существенно проще установка требуемой частоты, более наглядная индикация. Кроме того, цифровые генераторы имеют возможность автоматической перестройки частоты по заранее заданной программе и применения в сочетании с цифровыми средствами обработки информации.

Действие цифровых генераторов основано на принципе формирования числового кода с последующим преобразованием его в аналоговый гармонический сигнал. Последний аппроксимируется функцией, моделируемой с помощью ЦАП.

Самый простой вид аппроксимации – ступенчатая. Она заключается в представлении (замене) синусоидального колебания напряжением ступенчатой формы, весьма мало отличающейся от синусоидальной кривой (рис. 10.8, а).

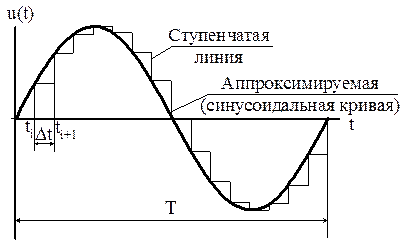
а)

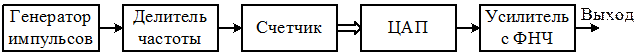
б)

Рисунок 10.8 – Цифровой генератор низких частот: а – ступенчатая аппроксимация, б – упрощенная структурная схема

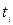Аппроксимируемое гармоническое напряжение дискретизируется во времени (равномерная дискретизация с шагом ) и в интервале, разделяющем два соседних момента времени и 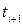синусоидальное колебание заменяется напряжением постоянного тока – ступенькой, высота которой равна значению аппроксимируемого напряжения в момент 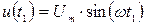. В результате такой замены вместо кривой синусоидальной формы получается ступенчатая линия, изображенная на рис. 10.8 а.

При имеющемся периоде 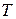гармонического колебания число ступенек 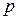, приходящихся на один период, определяется шагом дискретизации: 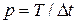. Если же из технических соображений число ступенек задано, то изменение шага дискретизации приводит к изменению периода формируемого напряжения, поскольку .

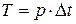Учитывая, что 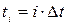, уравнение ступенчатой кривой можно представить в виде 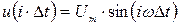или с учетом значения 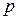и соотношения 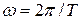записать в следующем виде:

.

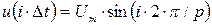Кроме того, ступенчатая кривая тем точнее приближается по форме к синусоиде (уменьшается погрешность аппроксимации), чем больше выбрано число ступеней 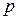. Когда это число достаточно велико, сформированное ступенчатое напряжение можно рассматривать как низкочастотное синусоидальное напряжение, искаженное в небольшой степени высокочастотной аддитивной помехой.

Спектральный анализ напряжения, полученного путем ступенчатой аппроксимации, показывает, что его спектр содержит гармонику основной частоты и ряд высших гармоник. При этом оказывается, что ближайшей к основной высшей гармоникой будет составляющая с номером 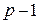, следующей – гармоника номера 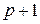, затем гармоники номеров и 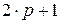и т.д. Например, при 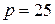и частоте напряжения 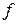основной гармоники ближайшими высшими гармониками будут 24-я, 26-я и 49-я, 51-я гармоники, т. е. напряжения частот 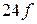; ; 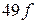и 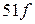. Такие соотношения между основной и высшими гармониками позволяют просто осуществить высококачественную фильтрацию, резко ослабляющую уровни высших гармоник, т.е. получить синусоидальное напряжение, характеризуемое достаточно малым коэффициентом нелинейных искажений.

Упрощенная структурная схема цифрового генератора, формирующего ступенчатую кривую напряжения, приведена на рис. 10.8 б. Импульсный кварцевый генератор вырабатывает периодическую последовательность коротких импульсов с периодом следования 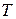. На выходе делителя частоты с регулируемым коэффициентом деления 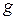получается периодическая последовательность импульсов с периодом следования 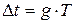, задающим шаг дискретизации. Импульсы поступают в счетчик емкостью 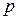. Кодовая комбинация, определяемая числом 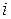импульсов, накопленных в счетчике, передается в схему ЦАП. Последний вырабатывает напряжение, соответствующее числу 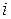, т.е. 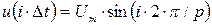. Таким образом формируются 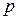ступенек аппрокимируемой кривой. После накопления 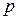импульсов счетчик переполняется и сбрасывается в нуль. С приходом (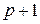)-го импульса начинается формирование нового периода ступенчатой кривой.

Частоту формируемого колебания при фиксированном числе ступенек 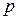регулируют, изменяя шаг дискретизации , что достигается изменением коэффициента деления 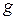делителя частоты.

Контрольные вопросы

1. Что называют измерительными генераторами сигналов?

2. Приведите классификацию измерительных генераторов.

3. Что называют генераторами гармонических колебаний? Приведите обобщенные структурные схемы измерительных генераторов.

4. На чем основан способ кварцевой стабилизации частоты?

Дата добавления: 2014-11-08