Введение. P-n-переходов полупроводниковых приборов

P-n-переходов полупроводниковых приборов

Исследование емкостных свойств

Требования к отчету

Отчет должен содержать:

1. Схему лабораторной установки.

2. Результаты исследований в виде таблиц и графиков в соответствии с п.3.

3. Формулы, по которым проводились расчеты, и примеры расчетов по пунктам 4,6,7,8,9.

4. Выводы по работе.

Контрольные вопросы

1. Чем обусловлена асимметричная проводимость р-n-перехода?

2. Чем определяется контактная разность потенциалов? Как она изменяется с увеличением степени легирования р-n-областей перехода?

3. Объясните температурную зависимость контактной разности потенциалов.

4. Почему с ростом обратного напряжения ток насыщения остается неизменным?

5. Как и почему изменяется ток насыщения с температурой? Как он зависит от ширины запрещенной зоны, степени легирования?

6. Как изменяется с понижением температуры доля тока насыщения в обратном токе через р-n-переход?

7. В чем отличие ВАХ реального диода от ВАХ р-n-перехода?

8. Почему с увеличением температуры ухудшаются выпрямительные свойства диода?

9. Почему у кремниевых диодов не бывает насыщения тока при обратном смещении?

10. Почему кремниевый диод может работать при более высоких температурах, чем германиевый?

11. Какие физические процессы происходят в выпрямительных диодах при прямом и обратном напряжениях?

12. Почему в цепях схем исследования прямых и обратных ветвей ВАХ диода амперметры и вольтметры включены по разному?

13. Чем отличаются ВАХ диодов с толстой и тонкой базами?

14. Почему по распределению неосновных носителей заряда в базе диода можно судить о величине плотности тока через диод?

15. Как влияет процесс рекомендации носителей в р-n-переходе диода на его ВАХ?

Литература

1. Ю.А. Байков, В.М. Кузнецов “Физика конденсированного состояния” М, Бином, 2011.

2. Г.И. Епифанов “Физика твёрдого тела” СП. б. Лань. 2009.

3. В.Л. Матухин, В.Л. Ермаков “ Физика твёрдого тела ” СП. б. Лань. 2009.

4. В.В. Пасынков, Чиркин Л.К. Полупроводниковые приборы. ВШ, М., 2014

Целью работы является изучение емкостных свойств p-n-перехода, проявляющихся при приложении к нему переменного сигнала, а также выяснение влияния на емкостные свойства режима работы р-n-перехода по постоянному напряжению.

В вводной части работы рассматриваются основные положения теории, описывающей емкостные свойства р-n-перехода. В практической части работы осваиваются измерение емкости р-n-перехода с помощью метода емкостно-омического делителя, определение концентрации примесей в слаболегированной области или градиента концентрации в области перехода.

В зависимости от закона изменения концентрации примеси в пограничной области между двумя полупроводниками с различным типом проводимости различают резкие или ступенчатые переходы (рис.5.1, 5.2) и большое разнообразие плавных, которые в ряде случаев могут считаться линейными, т.е. переходами, в области объемного заряда которых концентрация примеси меняется по линейному закону (рис.5.3). В принципе можно не только представить себе, но и в ряде случаев практически осуществить значительно более сложные профили изменения концентрации примеси, чем и занимается физика и техника полупроводниковых приборов, называемых варикапами.

Однако при всем многообразии различных видов р-n-переходов можно отметить общее, присущее всем р-n-переходам свойство: в области объемного заряда, как правило, пренебрежимо мала концентрация подвижных носителей заряда - электронов и дырок (см.рис.5.1).

Во всяком случае относительно легко выделить те области слоя пространственного заряда, где концентрация электронов и дырок пренебрежимо мала (см.рис.5.2). Исследование структуры слоя объемного заряда проводится с помощью уравнения Пуассона. В настоящей работе подробности этого анализа опускаются. Отметим, однако, наиболее важные предпосылки и итоги анализа.

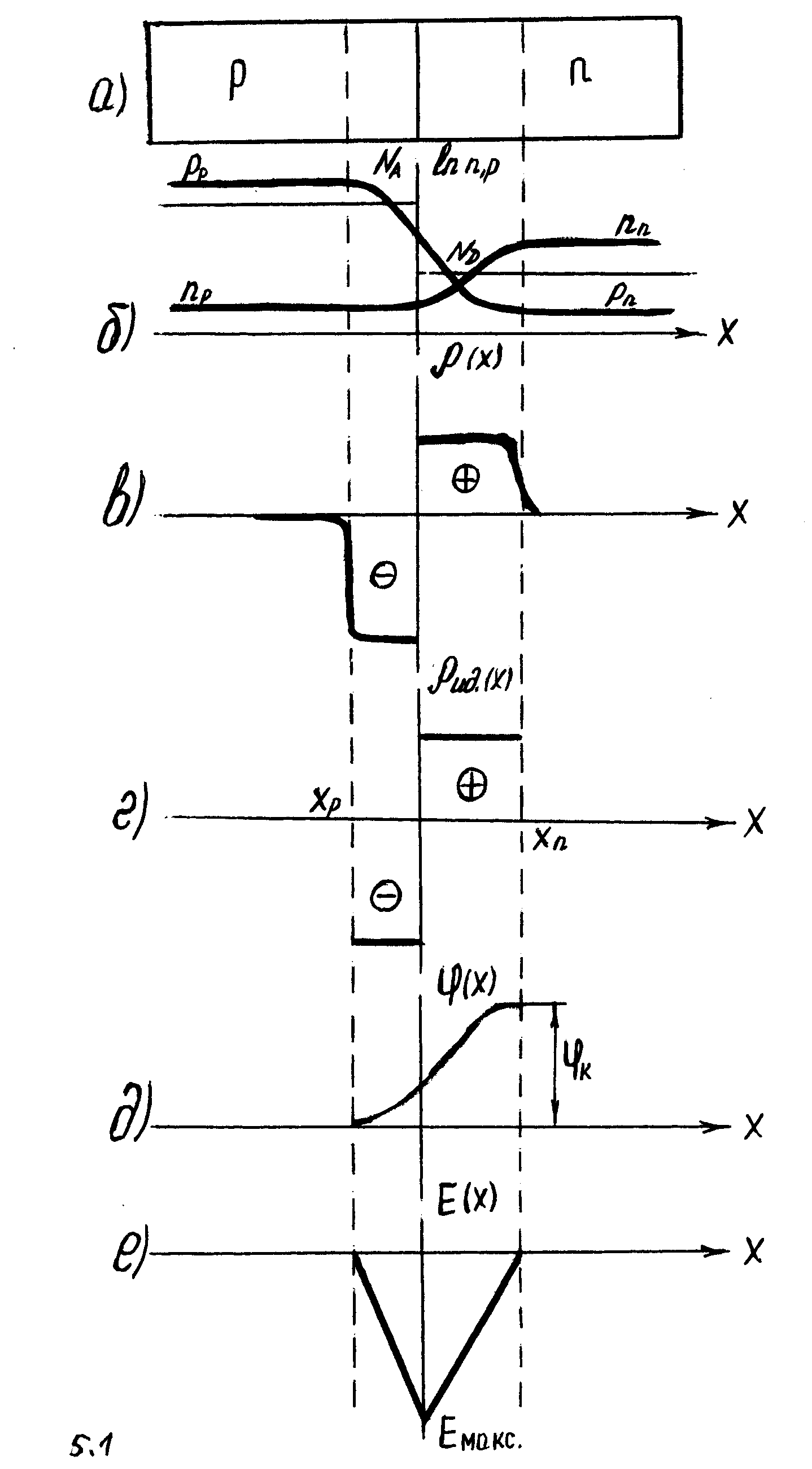
Рисунок 5.1− Резкий p-n- переход: а - структура, б - распределение примеси и концентрации подвижных носителей, в, г - распределение плотности объемного заряда (реальное и идеализация), д - распределение потенциала, е – распределение напряженности электрического поля

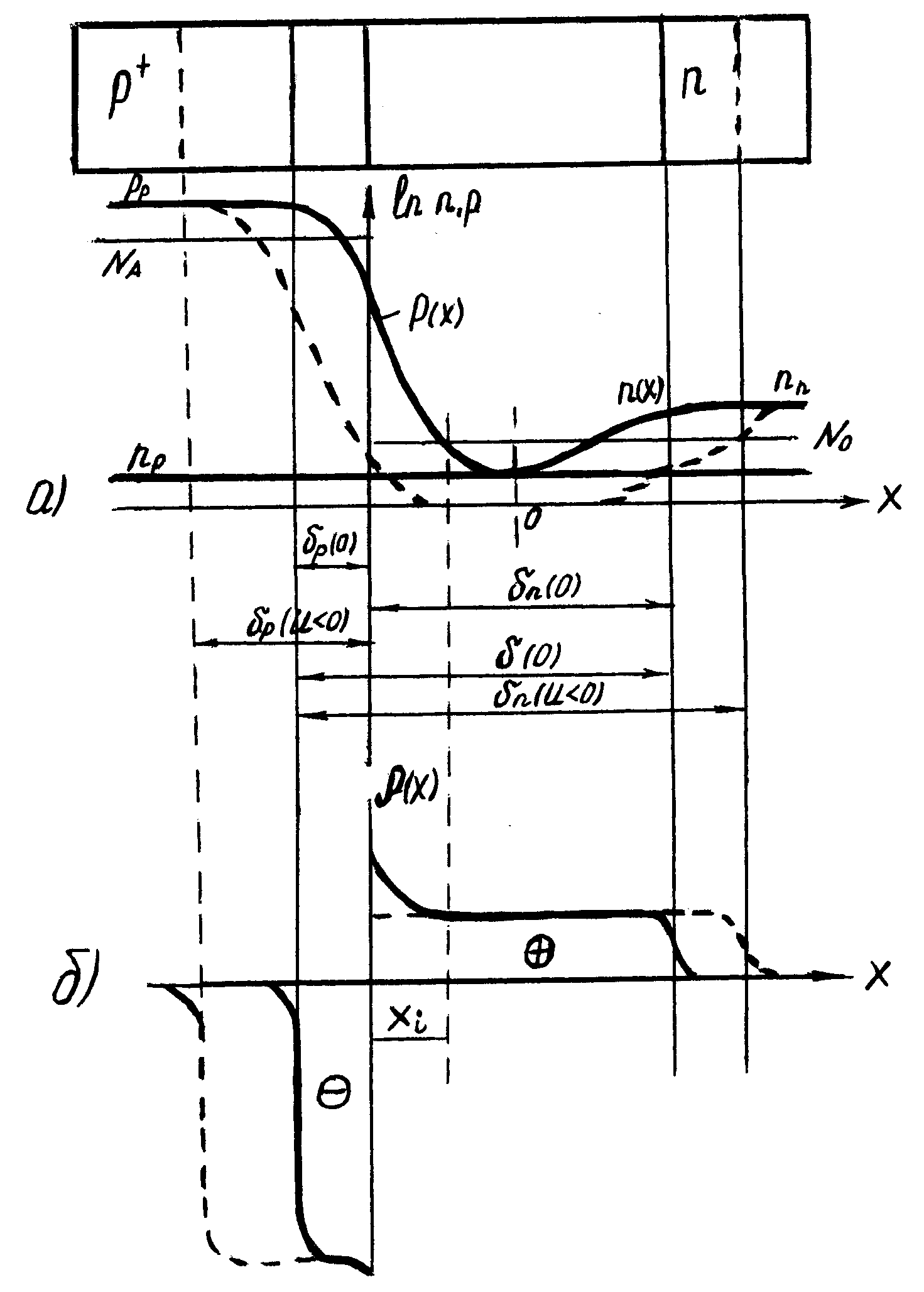
Рисунок5.2 − Распределение концентрации подвижных носителей (а) и плотности объемного заряда (б) в резком несимметричном p⁺-n- переходе (сплошные линии) при U=0 и пунктирные линии (обратное смещение при U<0)

1. Чаще всего рассматривается область объемного заряда, полностью лишенная подвижных носителей заряда. Соответствующая модель называется моделью истощенного слоя.

2. Поскольку область объемного заряда представляет собой своеобразный диполь, то на этом диполе электростатический потенциал имеет скачок на величину контактной разности потенциалов j_к.

3. Поскольку предположили, что область объемного заряда не содержит подвижных носителей заряда, то в первом приближении проводимость ее равна нулю и, следовательно, все приложенное извне напряжение прикладывается к слою объемного заряда, т.е. скачок электростатического потенциала при приложении внешнего смещения меняется и становится равным (j_к ± U) (рис.5.4).

4. Модель истощенного соля р-n-перехода позволяет вычислить конечную толщину слоя объемного заряда, которая зависит как от закона изменения примеси в переходном слое, так и от внешнего напряжения (рис.5.5). Например, толщина слоя объемного заряда резкого р-n-перехода определяется по формуле

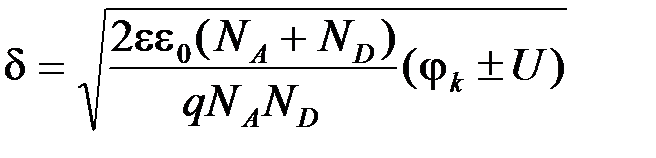. (5.1)

В частном случае, при N_А >>N_D (или наоборот N_D>>N_A) из соотношения (5.1) можно формальным путем получить выражение для толщины слоя объемного заряда резкого несимметричного (обозначаемого р⁺-n-перехода, соответственно n⁺-р) перехода

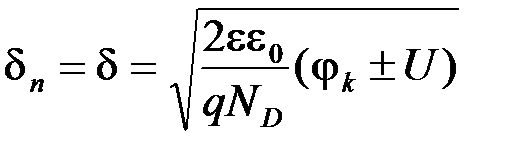. (5.2)

Сравнивая выражения (5.1) - (5.3), можно отметить, что в случае резкого р-n-перехода имеет место более сильная зависимость толщины слоя объемного заряда от внешнего напряжения, чем в случае линейного закона распределения примесей.

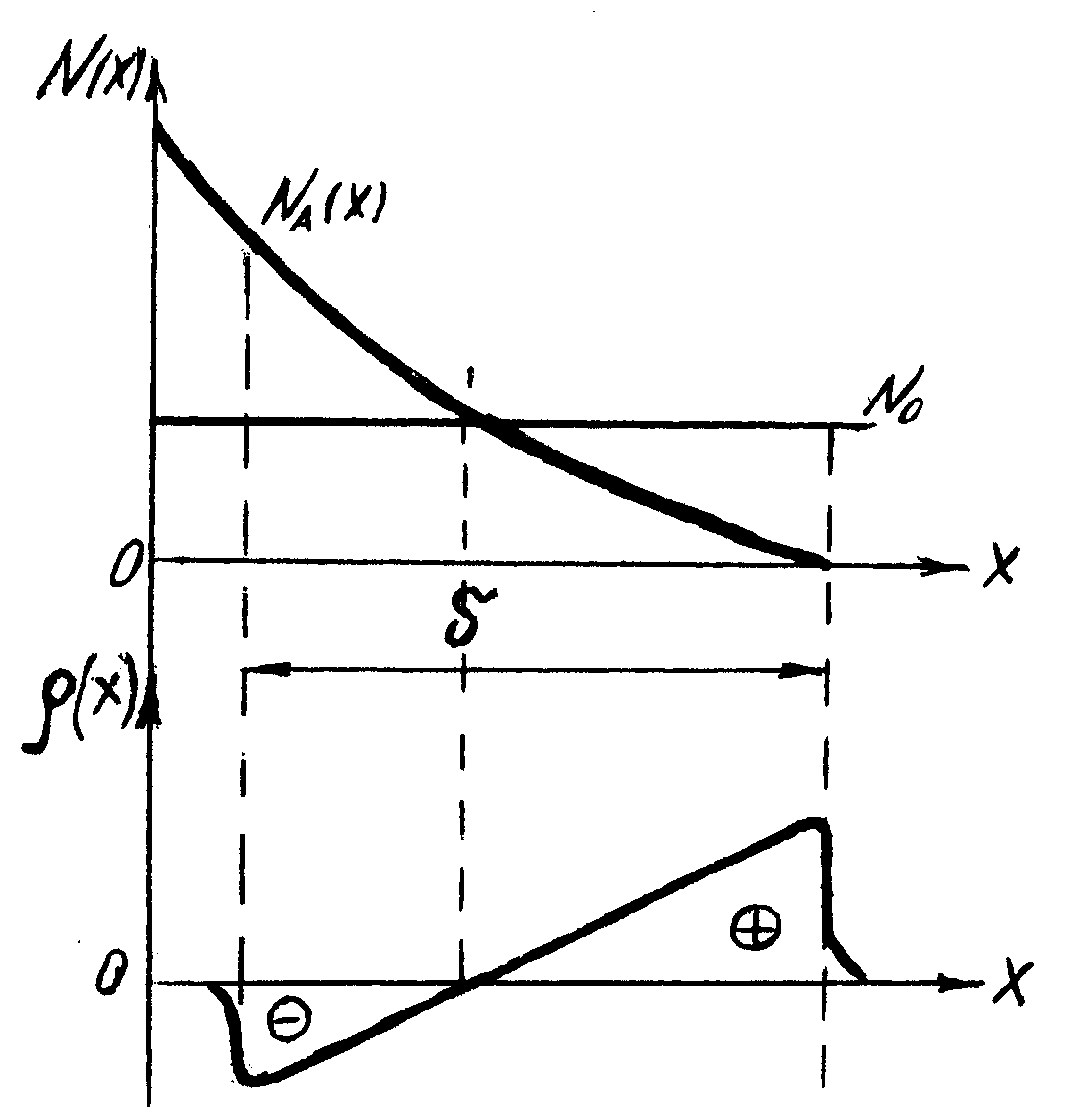
Рисунок5.3 − Распределение концентрации примеси и плотности объемного заряда в плавном p-n-переходе, образованном при диффузии акцепторов в электронный проводник.

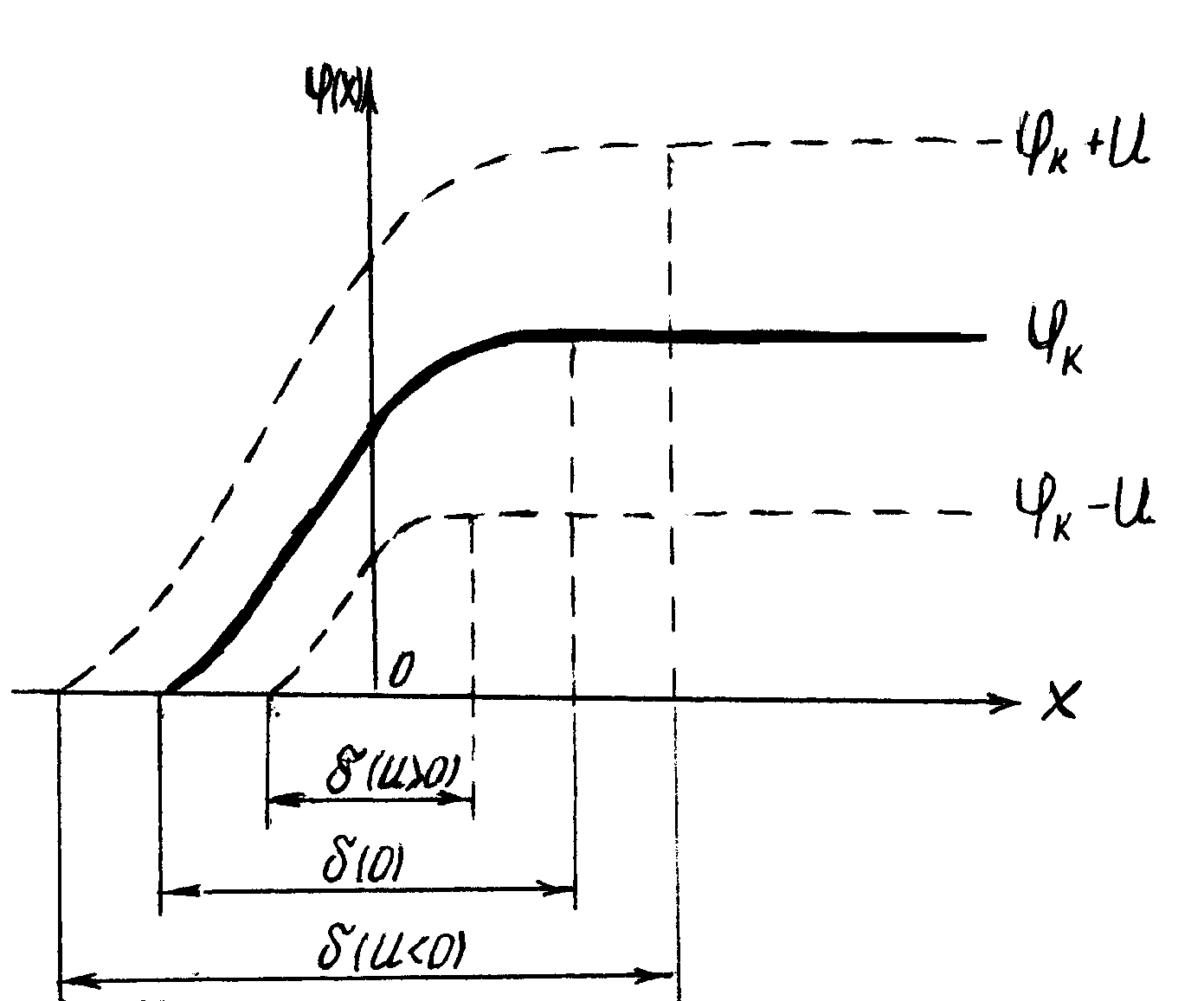
Рисунок5.4 − Изменение толщины слоя объеного заряда и потенциального барьера при приложении внешнего напряжения к p-n- переходу

Физическая же причина, объясняющая факт зависимости d = f(U), является общей для всех видов р-n-переходов и заключается в том, что под действием внешнего напряжения подвижные носители либо отсасываются из пограничной части области объемного заряда (тогда обнажаются новые слои нескомпенсированных доноров или акцепторов) и толщина слоя объемного заряда возрастает (обратное смещение U<0), либо подвижные носители, наоборот, направляются внутрь области объемного заряда, компенсируют определенное количество зарядов примеси и толщина слоя объемного заряда уменьшается (прямое смещение U>0) (см.рис.5.4).

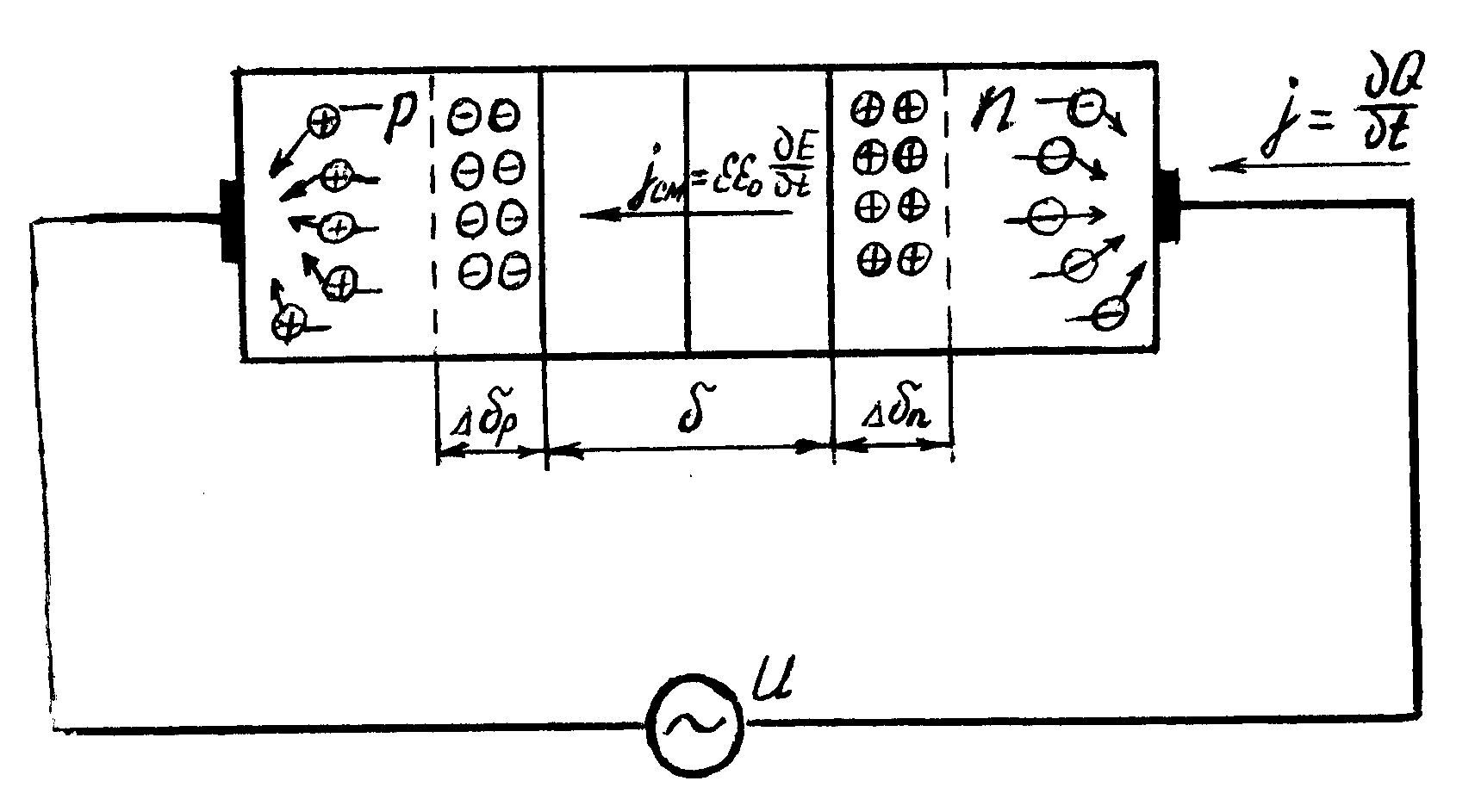
Рисунок 5.5 − Схема протекания тока смещения в области объемного

заряда p-n- перехода

Как указано выше, в модели истощенного слоя предполагается, что внутри слоя объемного заряда нет подвижных носителей заряда. В этом смысле область объемного заряда р-n-перехода аналогична области диэлектрика между обкладками конденсатора.

Как известно при подведении к конденсатору переменного напряжения в цепи потечет переменный ток. Этот ток, связанный с непрерывной перезарядкой конденсатора, называется током смещения и математически описывается формулой

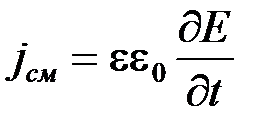. (5.4)

В проводниках, подводящих напряжение к конденсатору, протекает обычный ток проводимости, который связан с движением электронов, "откачиваемых" с одной из пластин конденсатора и направляющихся к другой.

Для плоского конденсатора электрическое поле Е постоянно и равно

E = U/d, (5.5)

где d - расстояние между пластинами.

Подставляя выражение (5.5) в (5.4), находим

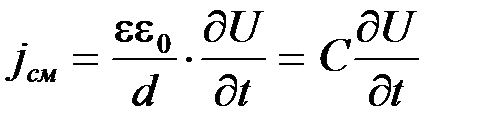; (5.6)

здесь С - емкость плоского конденсатора.

Аналогичным способом обстоит дело и в р-n-переходе. При приложении переменного напряжения к р-n-переходу в цепи потечет переменный ток. В первом приближении мы пренебрегаем движением подвижных носителей над потенциальным барьером (это движение связано с протеканием тока проводимости), а рассматриваем только ток смещения, определяемый формулой (5.4) В данном случае в отличие от плоского конденсатора поле Е зависит от координаты, и это не позволяет автоматически перейти от формулы (5.4) к формуле (5.6). Однако простое соображение показывает, что несмотря на то, что Е непостоянно в области объемного заряда, ток смещения остается постоянным во всей цепи области объемного заряда, так как общий ток во всей цепи постоянен, а внутри области объемного заряда нет другого тока, кроме тока смещения. В этом случае ток смещения может быть записан в виде

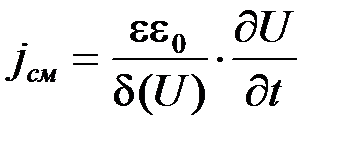. (5.7)

Так же, как и в случае плоского конденсатора, коэффициент пропорциональности обозначается как

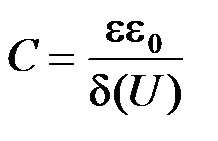. (5.8)

Эту емкость называют зарядной (барьерной) емкостью р-n-перехода. (Поскольку мы рассматриваем плотность тока смещения, то и емкость мы получили на единицу площади). Во внешней цепи протекает ток проводимости

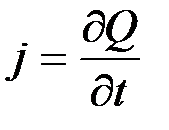. (5.9)

Сравнивая этот ток с током смещения, находим

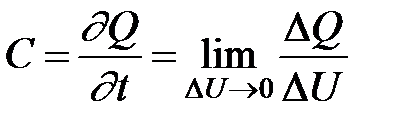. (5.10)

Заметим, что заряд DQ - есть либо заряд электронов, которые содержатся в слое толщиной Dd_n, либо равный ему заряд дырок, которые содержатся в слое толщиной Dd_р. Поэтому формула (5.10) может быть записана в виде

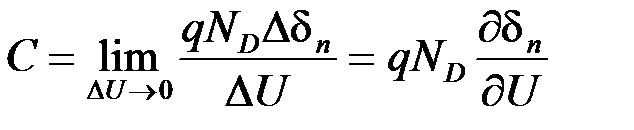. (5.11)

Подставляя в формулу (5.11) выражение для d_n (5.2), можно получить ту же самую формулу для емкости, которую получили раньше и которую часто записывают в виде

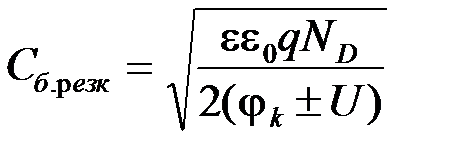. (5.12)

Для ступенчатого р-n-перехода с небольшой разницей N_A и N_D емкость определяется как

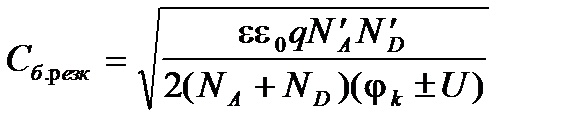. (5.13)

Для резкого несимметричного р-n-перехода часто используется формула

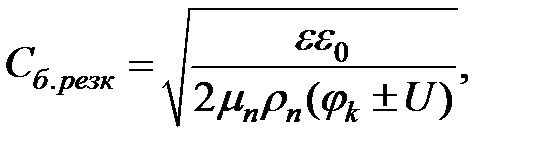, (5.14)

где m_n - подвижность электронов,

r_n - удельное сопротивление.

Для р-n-перехода с линейным законом распределения примеси зарядная емкость может быть представлена формулой

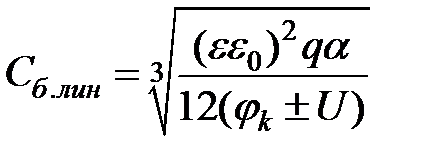. (5.15)

Как было указано выше, два случая законов распределения концентрации примеси в области объемного заряда - ступенчатое и линейное распределение, не исчерпывают всех возможных случаев и сами по себе являются идеализациями. Специальными методами могут быть осуществлены другие профили распределения примесей. Интересным представляется случай обратного градиента концентрации примеси, когда по мере увеличения толщины запирающего слоя концентрация примесей у его границ уменьшается. Такие р-n-переходы называются сверхрезкими потому, что для них характерно еще более резкое уменьшение емкости с ростом обратного напряжения, чем для резкого р-n-перехода (такие переходы используются для создания варикапов с высоким коэффициентом перекрытия, который представляет собой отношение максимальной и минимальной емкостей варикапа, соответствующих минимальному и максимальному приложенным напряжениям).

Рассмотрим, что могло бы дать экспериментальное исследование зависимости барьерной емкости от напряжения. По своему существу расчетные формулы (5.12-5.15) могут быть использованы лишь при обратных смещениях, поскольку при их выводе предполагалось, что через слой объемного заряда протекает только ток смещения и не протекает ток проводимости.

Перепишем выражения (5.13) и (5.15) в виде:

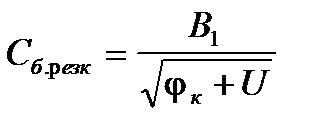, (5.16)

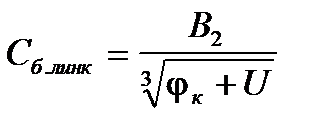, (5.17)

Логарифмируя эти выражения, получаем:

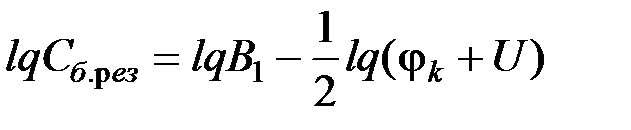, (5.18)

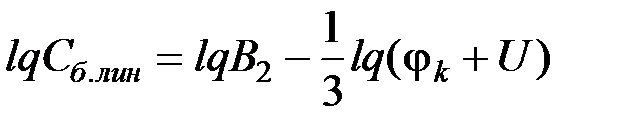. (5.19)

Таким образом, построение экспериментальной вольтфарадной характеристики в логарифмическом масштабе позволяет сделать вывод (по тангенсу угла наклона) о том, является переход резким или линейным.

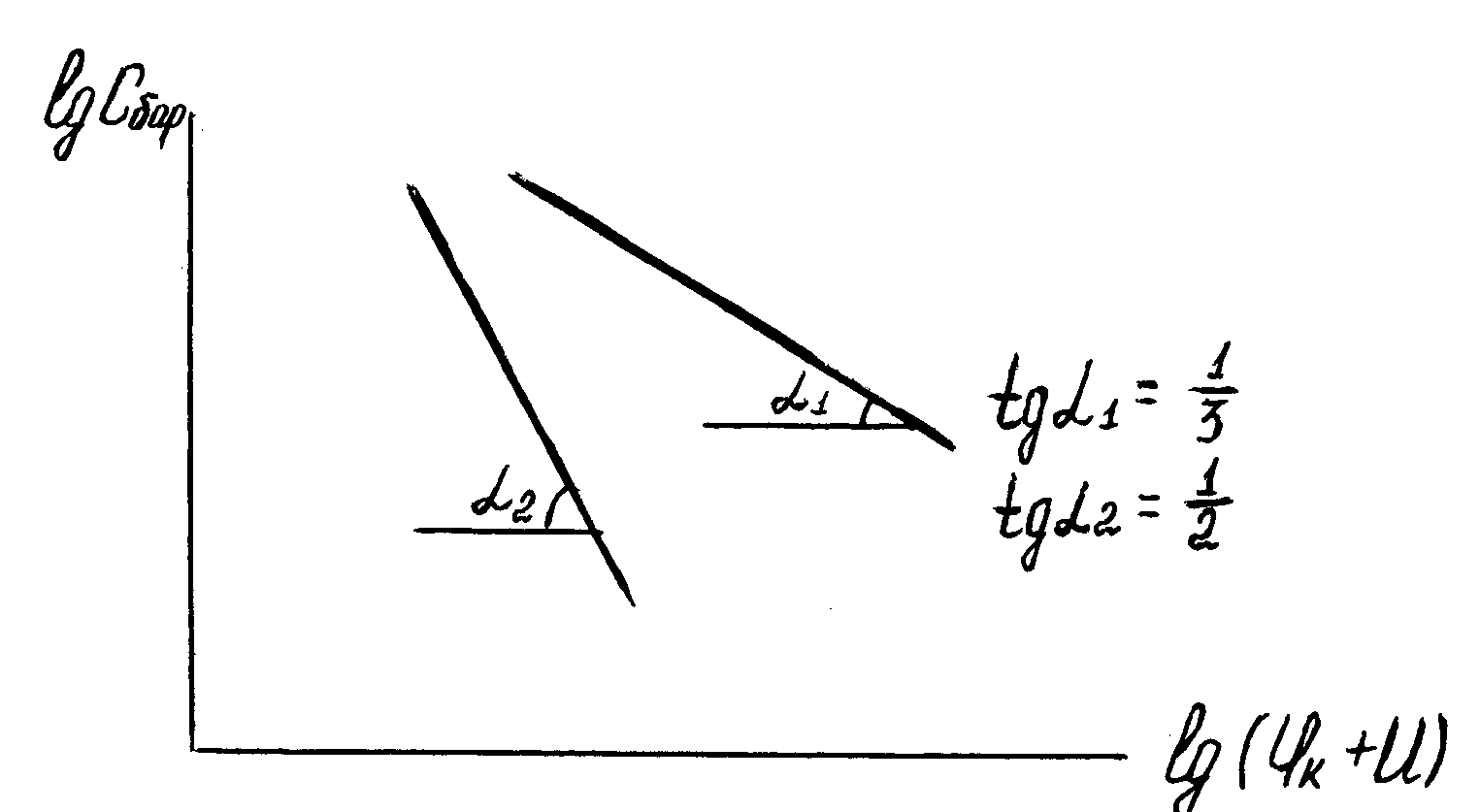
Рисукок5.6 − Зависимость C=f(U), построенная в логарифмическом масштабе для резкого и плавного p-n- переходов

Строго говоря, для построения графика в логарифмическом масштабе необходимо знать контактную разность потенциалов. Однако, как правило, j_к лежит в пределах 0,3-0,6 В, в то время как эксперимент проводится при напряжениях /U/>2В, поэтому при построении графика 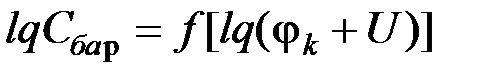величиной j_к можно пренебречь. Дальнейшая обработка экспериментальной зависимости позволяет определить величину j_к. Действительно, перепишем формулы (5.16) и (5.17) в виде:

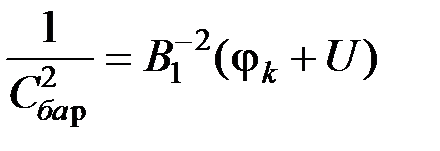, (5.20)

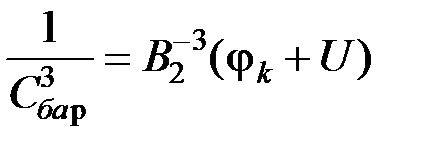, (5.20)

где , ,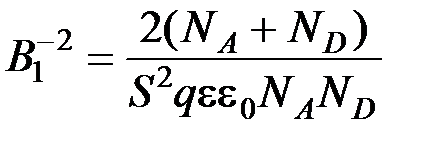

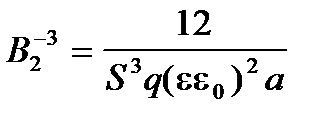S - площадь перехода.

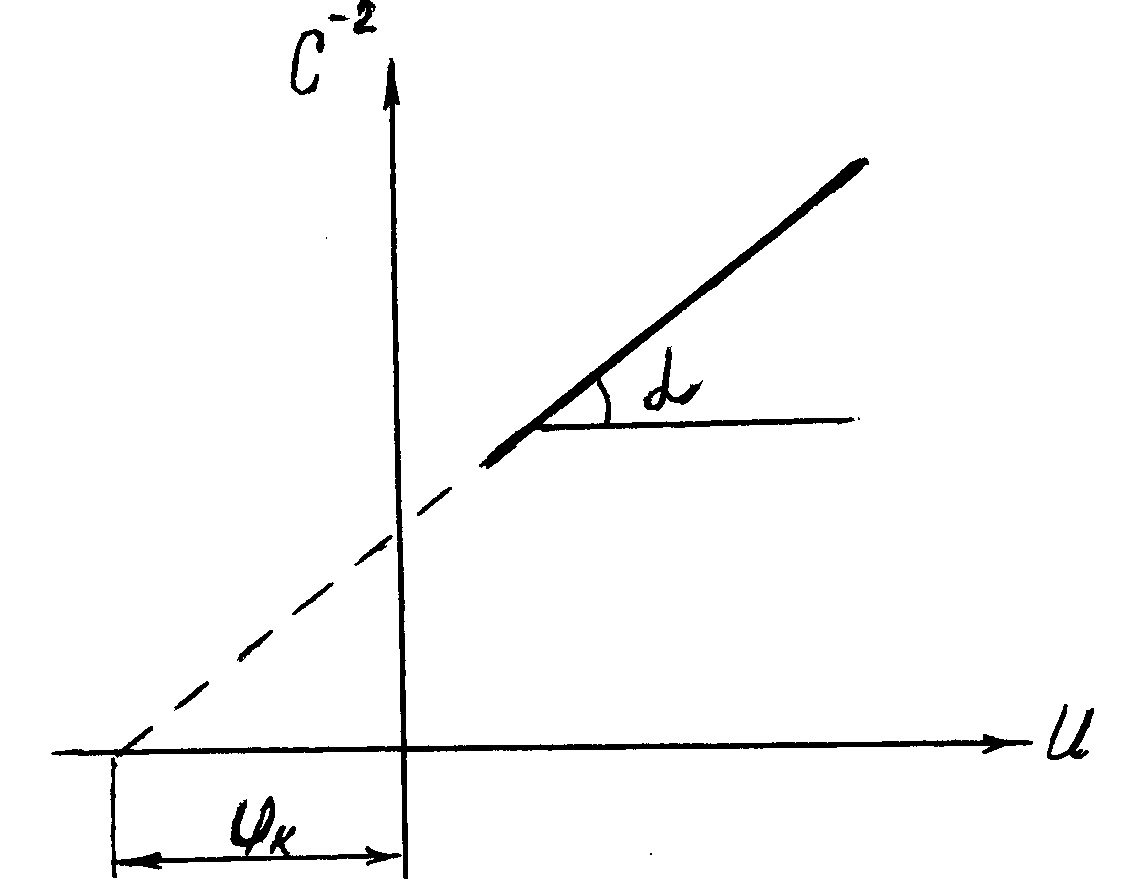
Рисунок 5.7 − Зависимость С ^-2 = f(U) для резкого p-n- перехода.

Построение вольфарадной характеристики в координатах С_бар^-2 = f(U) для резкого перехода (рис.5.7) позволяет по тангенсу угла наклона определить концентрацию одной из примесей, если известна другая (для р⁺-n-перехода сразу определяется концентрация N_D, для n⁺-р-концентрация N_A), а построение характеристики в координатах С_бар^-3 = f(U) для линейного перехода позволяет определить градиент концентрации а. Кроме того, аппроксимация прямолинейного графика до пересечения с осью абсцисс дает напряжение отсечки, равное контактной разности потенциалов как для резкого, так и для линейного переходов. Если закон распределения концентрации примеси более сложный, то исследование вольтфарадной характеристики позволяет определить профиль распределения концентрации примеси. Часто решается и обратная задача, т.е. необходимо заранее выяснить, какой закон распределения концентрации примеси должен иметь место, чтобы получить требуемый закон изменения емкости от напряжения.

В заключении отметим, что барьерная емкость, исследованием которой мы занимались, не единственная емкость, определяющая реактивные свойства р-n-перехода. При смещениях р-n-перехода в прямом направлении, кроме емкостного эффекта, обусловленного протеканием тока смещения в области объемного заряда, возникает другой емкостной эффект, описываемый с помощью так называемой диффузионной емкости, связанной с явлением инжекции. Протекание прямого тока через переход сопровождается попаданием неосновных носителей заряда - дырок в n-область, а электронов в р-область. Процесс введения неосновных носителей заряда называется инжекцией. Принципиальной особенностью поведения инжектированных носителей заряда является их сравнительно большое время жизни до рекомбинации с основными носителями заряда.

Если в течение времени жизни носителей напряжение на переходе изменить с прямого (при котором происходит инжекция) на обратное, то инжектированные носители заряда могут быть вновь возвращены через переход в ту область, из которой они пришли. Этот процесс называется экстракцией носителей заряда.

Чем больше прямой ток через переход, тем больше инжектируется носителей заряда, следовательно, тем большее их количество может быть экстрагировано при изменении полярности напряжения и пройдет в виде импульса тока во внешней цепи.

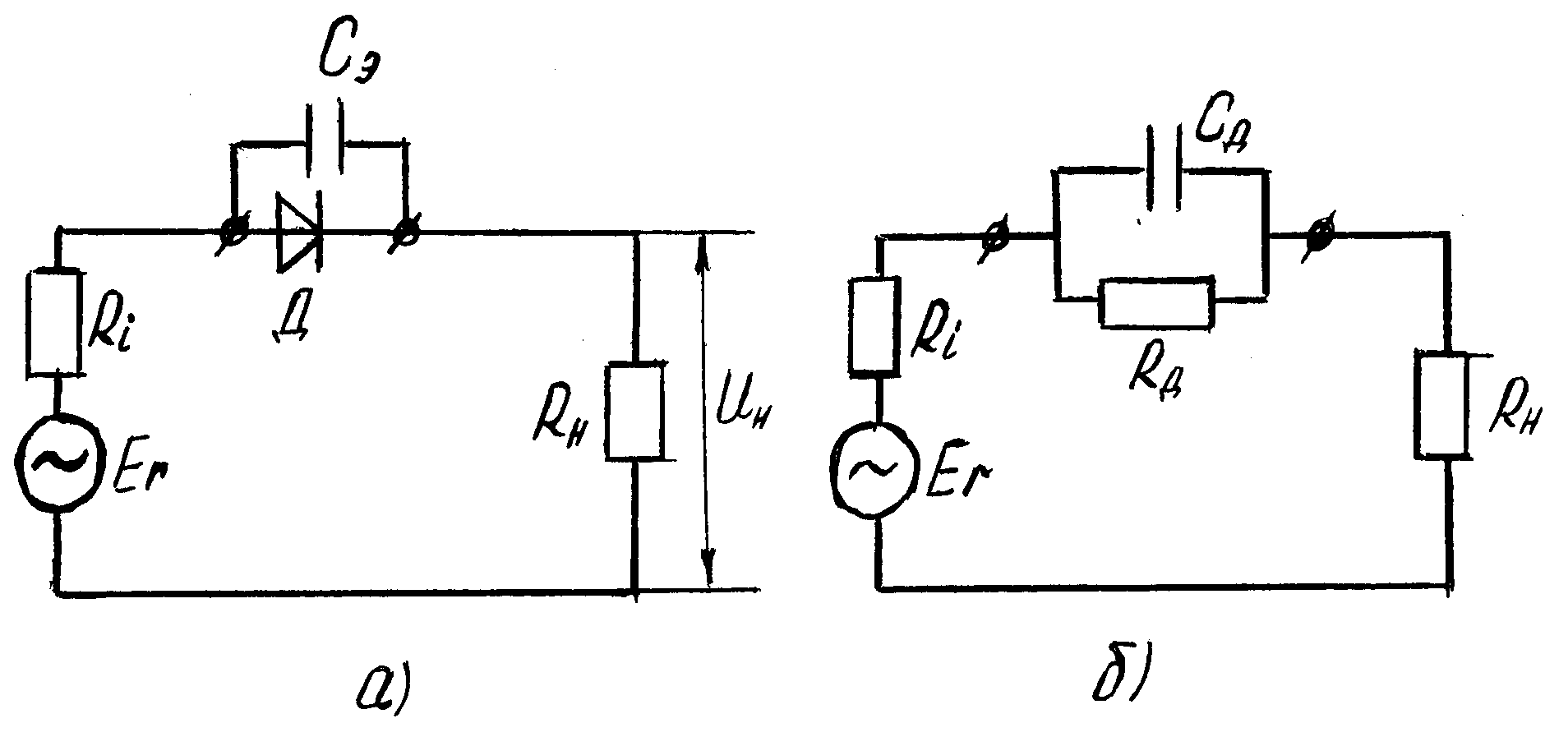
Рисунок5.8 − Схема измерения емкости p-n- перехода методом емкостно - омического делителя: а - включение диода в схему, б - эквивалентная схема перехода.

Описанные процессы аналогичны заряду и разряду конденсатора некоторой емкости. Обусловленная инжекцией неосновных носителей заряда емкость перехода называется диффузионной.

Из соотношения для вольтамперной характеристики р-n-перехода

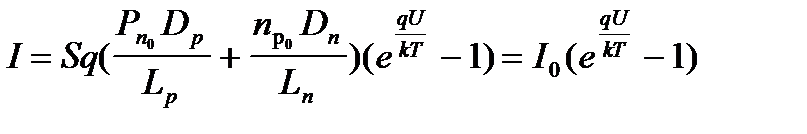(5.22)

можно сделать вывод, что доля g_р тока, переносимого одним типом носителей заряда (например, дырками), по отношению к полному току равна

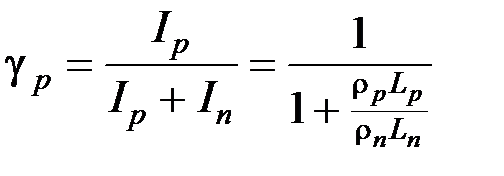(5.23)

(студентам предлагается самим вывести это соотношение).

Величина g_р называется коэффициентом инжекции. Если выполняется условие r _p << r _n, то g_р» 1. Это означает, что полный инжектированный заряд почти целиком образуется дырочной составляющей тока. При этих условиях выражение вольтамперной характеристики принимает вид

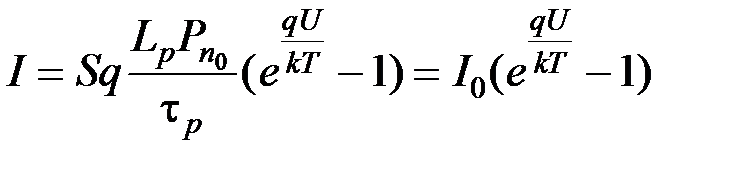. (5.24)

Используя соотношение для избыточной концентрации неосновных носителей заряда (дырок или электронов) на границе от приложенного к переходу внешнего напряжения

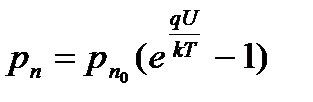, (5.25)

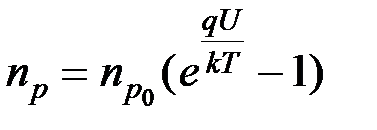, (5.26)

можно сделать вывод о том, что величина 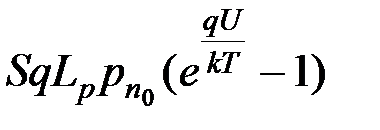в выражении (5.24) представляет полный заряд Q _р, образуемый инжектированными дырками в n-области. Ток через переход будет равен

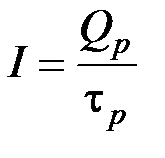. (5.27)

Из соотношения (5.27) легко получить выражение для дифузионной емкости перехода

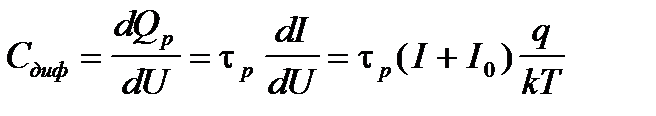. (5.28)

Как видим, величина диффузионной емкости пропорциональна току через переход. Она становится малой, когда на переход подано обратное напряжение, т.е. при I» -I₀. В этом случае основную роль играет барьерная емкость перехода С_бар. Наоборот, при больших прямых токах емкость перехода определяется величиной диффузионной емкости С_диф, которая значительно превышает барьерную. Например, если t_р = 5 мкс, I = 10 мА, то С_диф = 2 мкф. Такие значения на несколько порядков превосходят величину барьерной емкости. Диффузионная емкость зависит от частоты переменного сигнала; эта зависимость особенно заметна на частотах, соизмеримых с временем жизни неосновных носителей в базе диода.

Барьерная емкость остается постоянной вплоть до частот, определяемых максвелловским временем релаксации 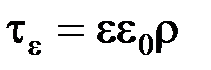, величина которого в зависимости от удельного сопротивления r обычно лежит в пределах 10^-11 - 10^-15 с. Поэтому в диапазоне частот от низких до частоты диэлектрической релаксации материала 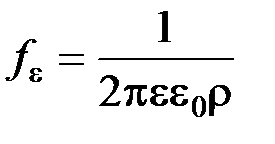, т.е. до 10¹¹- 10¹⁵ Гц барьерная емкость практически не зависит от частоты. Однако этот вывод справедлив лишь в том случае, если в слое объемного заряда нет примесных центров с глубокими уровнями, в противном случае наблюдается частотная зависимость барьерной емкости, обусловленная инерционностью процесса заряда и разряда этих глубоких центров.

Дата добавления: 2014-11-20