Свойства дисперсии

Вычисление дисперсии

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины 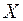и квадратом ее математического ожидания.

Доказательство. С учетом того, что математическое ожидание и квадрат математического ожидания – величины постоянные, можно записать:

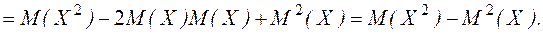
Применим эту формулу для рассмотренного выше примера:

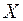
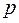
	0,0625	0,375	0,5625

1. Дисперсия постоянной величины равна нулю.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

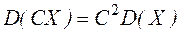
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

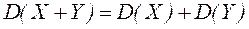
4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

Справедливость этого равенства вытекает из свойства 2.

Теорема. Дисперсия числа появления события 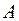в 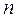независимых испытаний, в каждом из которых вероятность 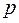появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в каждом испытании.

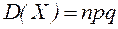
Дата добавления: 2014-11-20