
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Макроэкономика
|
|
|
|
ЖЖЖЖ
ЕЕЕ
ДДД
ГГГ
ББББ
АААА
А={-1,2,3,4,5,7} мен B={-1,0,5,6,7} жиындарының айырымын көрсететін өрнек: В {2,3,4}
 жиындары үшін келесі тұжырым дұрыс: 1)
жиындары үшін келесі тұжырым дұрыс: 1)  2)
2)  3)
3) 
 жиындары үшін келесі тұжырым дұрыс: 1)
жиындары үшін келесі тұжырым дұрыс: 1)  2)
2)  3)
3) 
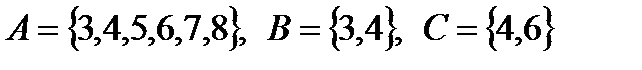 жиындары үшін келесі тұжырым дұрыс: 1)
жиындары үшін келесі тұжырым дұрыс: 1)  2)
2)  3)
3) 
А={3,4,5,6,7,8}, B={3,4}, C={4,6} жиындары үшін келесі тұжырым дұрыс: A A  B=A E B
B=A E B  A
A
А={4,5,6,7,8}, B={4,5,6}, C={7,8} жиындары үшін келесі тұжырым дұрыс: A A∩C=C
 жиындары үшін келесі тұжырым дұрыс: 1)
жиындары үшін келесі тұжырым дұрыс: 1)  2)
2)  3)
3) 
A=a,4,0 мен В=4,b жиындарының айырымын көрсететін өрнек: А ∩ В  А
А
 жиындарының бірігуі:
жиындарының бірігуі: 
A=[0; 1] және B=[1, 3] жиындарының бірігуі: В 0 ≤ x≤ 6
A=a,4,0 мен В=4,b жиындарының бірігуін көрсететін өрнек: А А  В
В  ∩ᴓ
∩ᴓ
А= а, 4,0 мен В= 4,6 жиындарының айырымын көрсететін өрнек: В) 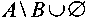
А= а,4,0 мен В= 4,6 жиындарының бірігуін көрсететін ернек: А)  В)
В)  С)
С)  D)
D) 
 нүктесі
нүктесі  функциясының 2 текті үзіліс нүкте болуы үшін келесі шарттың орындалуы жеткілікті: 1)
функциясының 2 текті үзіліс нүкте болуы үшін келесі шарттың орындалуы жеткілікті: 1) 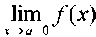 сол жақ шегі жоқ2)
сол жақ шегі жоқ2)  оң жақ шегі жоқ
оң жақ шегі жоқ
а е Е нүктесі  функциясының 1 - текті үзіліс нүкте
функциясының 1 - текті үзіліс нүкте
болса, онда:  В)
В) 
a  нүктесі f: E → R функциясының 1- текті үзіліс болса, онда: А
нүктесі f: E → R функциясының 1- текті үзіліс болса, онда: А  В
В 
a  нүктесі f: E → R функциясының 2- текті үзіліс нүкте болуы үшін келесі шарттың орындалуы жеткілікті: C
нүктесі f: E → R функциясының 2- текті үзіліс нүкте болуы үшін келесі шарттың орындалуы жеткілікті: C  сол жақ шегі жоқ F
сол жақ шегі жоқ F 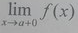 оң жақ шегі жоқ
оң жақ шегі жоқ
А және В жиындарының бірігуі деп E)А немесе В жиындарының ең олмағанда біреуіне тиісті болатын А  В жиынын айтамыз.
В жиынын айтамыз.
А және В жиындарының қиылысуы (A∩В) дегеніміз: А А жиынында да В жиынында да жататын элементтерден құрылған жиын
а саны 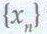 тізбегінің шегі болады, егер: A кез келген ε>0 саны үшін N номер табылып, барлық n>N үшін
тізбегінің шегі болады, егер: A кез келген ε>0 саны үшін N номер табылып, барлық n>N үшін  теңсіздігі орындалса D
теңсіздігі орындалса D 
А саны  функциясының а нүктесіндегі оң жақ шегі деп аталады, егер кез келген ε>0 саны үшін
функциясының а нүктесіндегі оң жақ шегі деп аталады, егер кез келген ε>0 саны үшін  саны табылып
саны табылып  теңсіздікті қанағаттандыратын барлық х үшін мына теңсіздік орындалса: А
теңсіздікті қанағаттандыратын барлық х үшін мына теңсіздік орындалса: А  С
С 
А саны  функциясының х→ а жағдайдағы шегі деп аталады, егер кез келген ε>0 саны үшін
функциясының х→ а жағдайдағы шегі деп аталады, егер кез келген ε>0 саны үшін  саны табылып мына
саны табылып мына  теңсіздікті қанағаттандыратын барлық х үшін мына теңсіздік орындалса: В
теңсіздікті қанағаттандыратын барлық х үшін мына теңсіздік орындалса: В 
А саны x→+∞ ұмтылғандағы f(x) функциясының шегі деп аталады, егер кез келген ε>0 саны үшін δ=δ(ε)>0 саны табылып, х>δ теңсіздігін қанағаттандыратын барлық х үшін келесі теңсіздік орындалса: B)  E)
E) 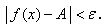 H)
H) 
А саны  функциясының х→ +
функциясының х→ +  жағдайдағы шегі деп аталады, егер кез келген ε>0 саны үшін
жағдайдағы шегі деп аталады, егер кез келген ε>0 саны үшін  саны табылып мына x>δ теңсіздікті қанағаттандыратын барлық х үшін мына теңсіздік орындалса: C - ε <
саны табылып мына x>δ теңсіздікті қанағаттандыратын барлық х үшін мына теңсіздік орындалса: C - ε <  - A < ε D |
- A < ε D |  - A | < ε
- A | < ε
Айталық D бірбайламды аймағының ішкі аймағы  берілсін. Нұсқалардың ішінен Руше теоремасын құрастыр? D аймағында
берілсін. Нұсқалардың ішінен Руше теоремасын құрастыр? D аймағында  голоморфты функция берілсін;
голоморфты функция берілсін;  аймағының
аймағының  шекарасында
шекарасында 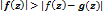 немесе
немесе  бағалаулары дұрыс болса,;
бағалаулары дұрыс болса,;  аймағының
аймағының  шекарасында
шекарасында  немесе
немесе  бағалаулары дұрыс болса,
бағалаулары дұрыс болса,
Айталық, 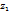 нүктесі
нүктесі  функциясының оқшауланған ерекше нүктесі болсын. Келесі сөйлемдер эквивалентті?
функциясының оқшауланған ерекше нүктесі болсын. Келесі сөйлемдер эквивалентті?  – жөнделетін ерекше нүкте;
– жөнделетін ерекше нүкте;  ақырлы шегі бар болады;
ақырлы шегі бар болады;
Айталық, 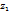 нүктесі
нүктесі  функциясының оқшауланған ерекше нүктесі болсын. Келесі сөйлемдер эквивалентті?
функциясының оқшауланған ерекше нүктесі болсын. Келесі сөйлемдер эквивалентті?  – полюс;
– полюс;  ақырсыз шегі бар;
ақырсыз шегі бар;
Айталық, 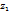 нүктесі
нүктесі  функциясының оқшауланған ерекше нүктесі болсын. Келесі сөйлемдер эквивалентті?
функциясының оқшауланған ерекше нүктесі болсын. Келесі сөйлемдер эквивалентті?  – елеулі ерекше нүкте;
– елеулі ерекше нүкте;  шегі жоқ
шегі жоқ
Айталық, 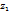 нүктесі
нүктесі  функциясының оқшауланған ерекше нүктесі болсын. Елеулі ерекше нүктенің критериі?
функциясының оқшауланған ерекше нүктесі болсын. Елеулі ерекше нүктенің критериі?  – елеулі ерекше нүкте;
– елеулі ерекше нүкте;  шегі жоқ
шегі жоқ
Айталық, 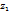 нүктесі
нүктесі  функциясының оқшауланған ерекше нүктесі болсын. Полюстің критериі?
функциясының оқшауланған ерекше нүктесі болсын. Полюстің критериі?  – полюс;
– полюс;  ақырсыз шегі бар
ақырсыз шегі бар
Айталық, 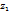 нүктесі
нүктесі  функциясының оқшауланған ерекше нүктесі болсын. Жөнделетін ерекше нүкте критериі?
функциясының оқшауланған ерекше нүктесі болсын. Жөнделетін ерекше нүкте критериі?  – жөнделетін ерекше нүкте;
– жөнделетін ерекше нүкте;  ақырлы шегі бар болады
ақырлы шегі бар болады
Ақырлы шегі бар тізбектер: 1) 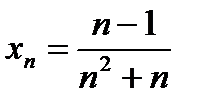 2)
2)  3)
3) 
Анықталмаған интеграл: ∫  A
A  C
C  E
E 
Анықталмаған интеграл: ∫  А
А 
Анықталмаған интеграл:  А
А  С
С  G
G 
Анықталмаған интеграл:  А)
А)  С)
С)  G)
G) 
Анықталмаған интеграл:  А)
А)  С)
С)  Е)
Е) 
Анықталмаған интегралды есептеңіз:  А)
А)  В)
В)  G)
G) 
Анықталмаған интегралды есептеңіз: 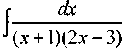 А)
А)  D)
D)  Е)
Е) 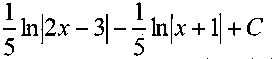
Анықталмаған интегралды есептеңіз:  С)
С)  F)
F)  3)
3) 
Анықталмаған интегралды есептеңіз: 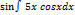 C
C  D
D  E
E 
Анықталмаған интегралды есептеңіз: ∫  А C - 4 ln| x +4|+ x В x -4 ln| x +4|+ C
А C - 4 ln| x +4|+ x В x -4 ln| x +4|+ C
Анықталмаған интегралды есептеңіз:  А
А 
Анықталмаған интегралды есептеңіз: ∫sin 5x cos xdx A  B
B  G
G 
Анықталмаған интегралды есептеңіз: ∫  C
C  F
F 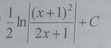 G
G 
Анықталмаған интегралды есептеңіз: ∫  A
A  D
D  E
E 
Барлық сан түзуінде анықталған функциялар: 1)  2)
2) 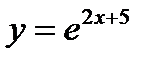 3)
3) 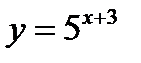
Бос жиынды көрсететін өрнек: 
Бүтін (Z), рационал (Q) және нақты (R) сандар жиыны үшін мына тұжырымдар дұрыс болады: В Кез
Келген рационал сан нақты сандар жиынының элементі С Кез келген бүтін сан нақты сандар
жиынының элементі
Бөліктеп интегралдауда  келесі интегралда қолданылады: 1)
келесі интегралда қолданылады: 1)  2)
2)  3)
3) 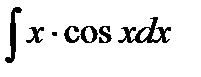
Бөліктеп интегралдауда  келесі интегралда қолданылады: 1)
келесі интегралда қолданылады: 1) 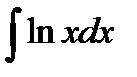 2)
2) 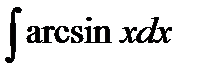 3)
3) 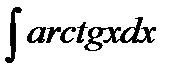
Гармоникалық функциялардың түйіндес қосы деп? Коши-Риман шартын қанағаттандыратын,; Екі
Гармоникалық функцияны айтады
Голоморфты функциялардың қасиеттері?  және
және  голоморфты функциялардың қосындысы,
голоморфты функциялардың қосындысы,
айырмасы, көбейтіндісі, сонмен қатар олардың қатынасы (  болғанда) және суперпозициясы
болғанда) және суперпозициясы
голоморфты функциялар; Голоморфты функциялар шексіз дифференциалданады; Голоморфты
функциялар үшін Кошидің интегралдық теоремасы мен Кошидің интегралдық формуласы орынды
Голоморфты функциялардың қасиеттерін көрсет? Голоморфты функциялар шексіз
дифференциалданады; Бірбайламды облыста голоморфты функцияның алғашқы бейнесі
голоморфты функция; Голоморфты функциялар үшін Кошидің интегралдық теоремасы мен
Кошидің интегралдық формуласы орынды
Голоморфты функциялардың қасиеттеріне қатысты қорытынды жаса? Егер 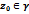 нүктесінде
нүктесінде 
Екі голоморфты функциялардың қатынасы түрінде берілсе; Сондай-ақ,  ; ал
; ал
 , онда;
, онда; 
Дифференциалды бином  мұндағы m,n,p - рационал сандар, келесі жағдайда
мұндағы m,n,p - рационал сандар, келесі жағдайда
интегралданады: D  F
F  G
G 
Дифференциалды бином  , мұндағы
, мұндағы  -рационал сандар, келесі жағдайда
-рационал сандар, келесі жағдайда
интегралданады: 1)  2)
2) 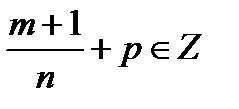 3)
3) 
Дифференциалдау ережесі: 1)  2)
2)  3)
3) 
Егер  және
және  функциялары дифференциалданатын болса, онда: 1)
функциялары дифференциалданатын болса, онда: 1)  2)
2)  3)
3) 
Егер  функциясы
функциясы 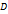 аймағында үзіліссіз және? Кез келген осы аймақтағы
аймағында үзіліссіз және? Кез келген осы аймақтағы  үшбұрыштың шекарасы
үшбұрыштың шекарасы  бойынша
бойынша
интегралы нөлге тең болса, онда;  голоморфты функция;
голоморфты функция;  жауаптары дұрыс
жауаптары дұрыс
Егер  функциясы қандайда бір
функциясы қандайда бір 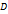 аймағында голоморфты болса, онда? Оның
аймағында голоморфты болса, онда? Оның  нақты
нақты
бөлігі бұл аймақта гармоникалық функция; Оның  жорамал бөлігі бұл аймақта гармоникалық функция
жорамал бөлігі бұл аймақта гармоникалық функция
Егер  функциясы қандайда бір
функциясы қандайда бір 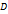 аймағында голоморфты болса, онда оның? Нақты бөлігі бұл аймақта
аймағында голоморфты болса, онда оның? Нақты бөлігі бұл аймақта
гармоникалық болады; Жорамал бөлігі гармоникалық функция болады;  аймағының ішкі аймағындағы;
аймағының ішкі аймағындағы;
 функциясы нөлдерінің санымен беттеседі
функциясы нөлдерінің санымен беттеседі
Егер В жиыны А жиынының ішкі жиыны болса, онда: D B  A
A
Егер f (x) =  берілсе, онда: B f- тақ функция D
берілсе, онда: B f- тақ функция D 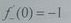 E
E 
Егер f (x) =  берілсе, онда: А f- жұп функция С функция x=0 нүктеде анықталмаған
берілсе, онда: А f- жұп функция С функция x=0 нүктеде анықталмаған
Егер  берілсе, онда: C f’_(0)-жоқ D ол -∞;+∞ аралығында үзіліссіз E f’ +(0)-жоқ
берілсе, онда: C f’_(0)-жоқ D ол -∞;+∞ аралығында үзіліссіз E f’ +(0)-жоқ
Егер  берілсе, онда:1) X > 0 нүктелерінде функция үзіліссіз2) х < 0 нүктелерінде функция
берілсе, онда:1) X > 0 нүктелерінде функция үзіліссіз2) х < 0 нүктелерінде функция
Үзіліссіз
Егер  берілсе, онда: С x>0 нүктелерінде функция үзіліссіз Е x<0 нүктесінің маңайында
берілсе, онда: С x>0 нүктелерінде функция үзіліссіз Е x<0 нүктесінің маңайында
функция үзіліссіз
Егер f функциясы a;b кесіндісінде үзіліссіз болса, онда: A осы кесіндіде оның ең кіші мәні бар D осы кесіндіде
оның ең үлкен мәні бар
Егер f функцияларының x˳ нүктесінде туындысы бар болса, онда: B 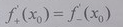 D
D 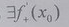 E f - периодты функция
E f - периодты функция
Егер f (x) =  функциясы берілсе, онда: C асимптотасы y=2, түзуі D оның ең кіші мәні f (0) =
функциясы берілсе, онда: C асимптотасы y=2, түзуі D оның ең кіші мәні f (0) =  E 0;+∞
E 0;+∞
аралығында өседі
Егер  функци^сы берілсе, онда: B (-∞;0) аралығында ойыс E 0;+∞ аралығында ол дөңес (график дөңестігі
функци^сы берілсе, онда: B (-∞;0) аралығында ойыс E 0;+∞ аралығында ол дөңес (график дөңестігі
жоғары бағытталған) F x=0 - оның иілу нүктесі
Егер  функциясы берілсе, онда: 1)ол(
функциясы берілсе, онда: 1)ол(  аралығында өседі2)функцияның асимптотасы жоқ3) (
аралығында өседі2)функцияның асимптотасы жоқ3) (
2;+∞) аралығында функция ойыс (дөңестігі темен бағытталған)
Егер  болса, онда: A
болса, онда: A  E
E  F
F 
Егер y=ln(x²+5)болса, онда y’(1) туындының мәні келесі аралыққа тиісті болады: D)(-1;+∞) G)[0;4] H)(0;+∞)
Егер y=3x²+x+1 болса, онда y  туындының мәні келесі аралыққа тиісті болады: D)(-1;+∞) E) (-2;1) G) [0;4]
туындының мәні келесі аралыққа тиісті болады: D)(-1;+∞) E) (-2;1) G) [0;4]
Егер  және
және  болса, онда: A
болса, онда: A 
Егер 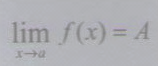 және C=const болса, онда: A
және C=const болса, онда: A  F
F 
Егер  шектері бар және олар ақырлы болса, онда: A
шектері бар және олар ақырлы болса, онда: A  D
D  шегі де бар
шегі де бар
Егер  шектері бар және олар ақырлы болса, онда: A f(x) + g(x) функциясы x=a нүктесінің
шектері бар және олар ақырлы болса, онда: A f(x) + g(x) функциясы x=a нүктесінің
маңайында шеңелген E 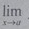 f(x) + g(x ) шегі де бар
f(x) + g(x ) шегі де бар
Егер  шектері бар болса, онда: В
шектері бар болса, онда: В 
Егер / функциясы a; b кесіндісінде үзіліссіз болса, онда: 1)осы кесіндіде оның ең кіші мэні бар2)осы кесіндіде оның
ең үлкен мәні бар
Егер/ функцияларының 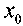 нүктесінде туындысы бар болса, онда: 1)
нүктесінде туындысы бар болса, онда: 1)  2)
2)  3) f — периодты
3) f — периодты
функция
Жинақты тізбектер: 1)  2)
2)  3)
3) 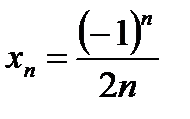
Жинақты тізбектер: D 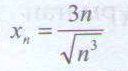
Жинақты тізбектер: C  D
D  E
E 
Жұп функциялар: 1)  2)
2)  3)
3) 
Лопиталь ережесін келесі шекті есептеуге қолдануға болады: B  C
C  D
D 
Модулдің максимум принципі? Аймақта голоморфты функция модулі ішкі нүктеде максимумға жетеді сонда тек
сонда ғана; Қашан функция тұрақты болса
Натурал (N), бүтін (Z) және рационал (Q) сандар жиыны үшін мына қатынастар дұрыс болады: С Z 
Нүктедегі голоморфты функцияның анықтамасы және оның бар болуының қажетті шарты- Нүктеде комплексті талдау мағынасында туындысы бар функция; Коши-Риман шарты
Нұсқалар арасынан бүтін функция анықтамасы мен кейбір қасиеттерін тап? Барлық комплекс жазықтықта голоморфты функция; Шексіз жинақталу радиусымен Тейлор қатарына жіктеледі; Ақырлы шектік нүктесіз нөлдері оқшауланған
Нұсқалар арасынан бүтін функция анықтамасы мен кейбір қасиеттерін тап? Барлық комплекс жазықтықта голоморфты функция; Тұрақты емес шенелген бүтін функциялар жоқ; Шексіз жинақталу радиусымен Тейлор қатарына жіктеледі
Нұсқалар арасынан Жозеф Лиувилль теоремасының тұжырымын құр? Бүтін функция; Өзінің аргументінің модулінің қандайда бір дәрежесінен жылдамырақ өспесе, онда; Көпмүшелік береді
Нұсқалар арасынан Кошидің интегралдық теоремасының тұжырымын құр?  аймағындағы кез келген гомотопты қисықтар бойынша;
аймағындағы кез келген гомотопты қисықтар бойынша;  аймағындағы голоморфты функция интегралы; Бір ғана мәнді қабылдайды
аймағындағы голоморфты функция интегралы; Бір ғана мәнді қабылдайды
Оқшауланған ерекше нүктелер басты бөліктегі қосылғыштардың мөлшеріне байланысты келесі түрлерге бөлінеді? Елеулі ерекше нүкте;  – ретті полюс; Жөнделетін ерекше нүкте
– ретті полюс; Жөнделетін ерекше нүкте
Рационал (Q), иррационал (I) және нақты (R) сандар жиыны үшін мына қатынастар дұрыс болады: А Q  С I
С I 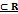
Рационал бөлшекті  келесі қарапайым бөлшектердің қосындысы ретінде жіктеуге болады: 1)
келесі қарапайым бөлшектердің қосындысы ретінде жіктеуге болады: 1)  2)
2)  3)
3) 
Рационал бөлшекті  келесі қарапайым бөлшектердің қосындысы ретінде жіктеуге болады: 1)
келесі қарапайым бөлшектердің қосындысы ретінде жіктеуге болады: 1)  2)
2)  3)
3) 
Р ационал бөлшекті  келесі қарапайым бөлшектердің қосындысы ретінде жіктеуге болады: 1)
келесі қарапайым бөлшектердің қосындысы ретінде жіктеуге болады: 1)  2)
2)  3)
3) 
Сан түзуінде үзіліссіз функциялар: 1)  2)
2)  3)
3) 
Тақ функциялар: 1)  2)
2)  3)
3) 
Туындының геометриялық мағынасы: C) tgß, мұнда ß - жанама мен Ох осінің арасындағы бұрыш
Шексіз аз тізбектер: 1) 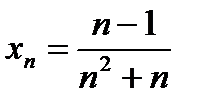 2)
2)  3)
3) 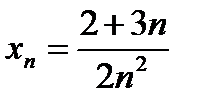
Шексіз үлкен тізбектер: 1)  2)
2)  3)
3) 
Шекті есептеңіз:  А
А  В
В 
Шекті Лопиталь ережесін қолданып есептеңіз:  C sin
C sin  E 1 F ln e
E 1 F ln e
Шекті Лопиталь ережесін қолданып есептеңіз:  A -0,5 B -
A -0,5 B -  F - sin
F - sin 
Шенелген бүтін функция? Тұрақты функция; Жауаптың с нұсқасы дұрыс; с нұсқасы дұрыс және біз Ж. Лиувилль теоремасының тұжырымына келдік
Функцияның туындысын есептеңіз: y = x arcsin x A  B
B 
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1174; Нарушение авторских прав?; Мы поможем в написании вашей работы!