Т а б л и ц а 3.4

Т а б л и ц а 3.3

Т а б л и ц а 3.2

Т а б л и ц а 3.1

Таблица переходов и входов автомата Мили

Входы xi	Состояния zk
z0	z1	…	…	…	zk
	Переходы
x1	φ (z0, x1)	φ (z1, x1)	…	…	…	φ (zk, x1)
x2	φ (z0, x2)	φ (z1, x2)	…	…	…	φ (zk, x2)
….	…..	….	….	….	….	….
	Выходы
x1	ψ (z0, x1)	ψ (z1, x1)	…	…	…	ψ (zk, x1)
x2	ψ (z0, x2)	ψ (z1, x2)	…	…	…	ψ (zk, x2)
….	…..	….	….	….	….	….

Таблица переходов и входов автомата Мили с тремя состояниями (z₀, z₁, z₂), двумя входными (x₁, x₂) и двумя выходными (y₁, y₂) сигналами

Входы xi	Состояния zk
z0	z1	z2
	Переходы
x1	z2	z0	z0
x2	z0	z2	z1
	Выходы
x1	y1	y1	y2
x2	y1	y2	y1

Описание работы F –автоматов Мура иллюстрируется табл.3.3, а пример табличного способа задания F –автомата Мура с пятью состояниями (z₀, z₁, z₂, z₃, z₄), двумя входными (x₁, x₂) и тремя выходными (y₁, y₂, y₃) сигналами приведён в табл.3.4.

Графический способ задания конечного автомата использует понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал x_k вызывает переход из состояния z_i в состояние z_j, то на графе автомата дуга, соединяющая вершину z_i с вершиной z_j, обозначается x_k. Для того чтобы задать функцию выходов, дуги графа необходимо отметить соответствующими выходными сигналами.

Отмеченная таблица переходов автомата Мура

Входы xi	Состояния zk
ψ (z0)	ψ (z1)	….	ψ (zk)
z0	z1	….	zk
x1	φ (z0, x1)	φ (z1, x1)	…	φ (zk, x1)
x2	φ (z0, x2)	φ (z1, x2)	…	φ (zk, x2)
…	…	…	…	…

Отмеченная таблица переходов автомата Мура с пятью состояниями (z₀, z₁, z₂, z₃, z₄), двумя входными (x₁, x₂) и тремя выходными (y₁, y₂, y₃) сигналами

Входы xi	Состояния zk
y1	y1	y3	y2	y3
z0	z1	z2	z3	z4
x1	z1	z4	z4	z2	z2
x2	z3	z1	z1	z0	z0

Для автоматов Мили эта разметка производится так: если входной сигнал x_k действует на состояние z_i, то, согласно сказанному, получается дуга, исходящая из z_i и помеченная x_k; эту дугу дополнительно отмечают выходным сигналом y = ψ (z_i, x_k). На рис. 3.35 приведён заданный ранее табл.3.2 граф F –автомата Мили.

Рис. 3.35. Граф автомата Мили

Для автоматов Мура аналогичная разметка графа такова: если входной сигнал x_k, действуя на некоторое состояние z_i автомата, вызывает переход в состояние z_j, то дугу, направленную в z_j и помеченную x_k, дополнительно отмечают выходным сигналом y = ψ (z_j, x_k). На рис. 3.36 приведён заданный ранее табл.3.4 граф F –автомата Мура.

Рис. 3.36. Граф автомата Мура

Матричный способ задания конечного автомата часто является более удобной формой. При этом матрица соединений автомата есть квадратная матрица C = [ c_ij ], строки которой соответствуют исходным состояниям, а столбцы – состояниям перехода.

В случае F –автомата Мили элемент c_ij = x_k / y_s, стоящий на пересечении i -ой строки и j -го столбца, соответствует входному сигналу x_k, вызвавшему переход из состояния z_i в состояние z_j, и выходному сигналу y_s, выдаваемому при этом переходе. Для автомата Мили, рассмотренного выше, матрица соединений имеет вид

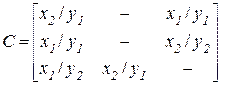. (3.34)

Если переход из состояния z_i в состояние z_j происходит под действием нескольких сигналов, элемент матрицы c_ij представляет собой множество пар «вход-выход» для этого перехода, соединённых знаком дизъюнкции.

Для F –автомата Мура элемент c_ij = x_k / y_s равен множеству входных сигналов на переходе (z_i, z_j), а выход описывается вектором выходов, i -я компонента которого – выходной сигнал, отмечающий состояние z_i. Для автомата Мура, рассмотренного выше, матрица соединений и вектор выходов имеют вид

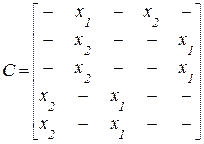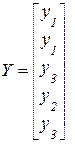; . (3.35)

Для детерминированных автоматов выполняется условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние. Это означает, что в графе автомата из любой вершины не могут выходить две и более дуг, отмеченных одним и тем же входным сигналом, а в матрице соединений в каждой строке входной сигнал не должен встречаться более одного раза.

Рассмотрим таблицу переходов и граф асинхронного конечного автомата. Для F –автомата состояние z_k называется устойчивым, если для любого входа x_i Î X, для которого φ (z_k, x_i) = z_k имеет место ψ (z_k, x_i) = y_k. Таким образом, F –автомат называется асинхронным, если каждое его состояние z_k Î Z устойчиво.

Ниже приведён пример асинхронного автомата Мура, заданного таблично (табл.3.5) и графически (рис.3.37).

Дата добавления: 2014-11-20