
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства определителей. 2 страница
|
|
|
|
 и
и 
 =
= 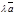 в координатной форме имеет вид
в координатной форме имеет вид
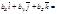
 . Из этого равенства следует наше утверждение, так как
. Из этого равенства следует наше утверждение, так как
 .
Верно и обратное.
Векторное произведение двух векторов
Предварительно введем понятие правой тройки векторов. Три вектора
.
Верно и обратное.
Векторное произведение двух векторов
Предварительно введем понятие правой тройки векторов. Три вектора  ,
,  ,
,  образуют правую тройку, если движение вектора
образуют правую тройку, если движение вектора  к вектору
к вектору  по меньшему углу совершается против часовой стрелки, при наблюдении с конца вектора
по меньшему углу совершается против часовой стрелки, при наблюдении с конца вектора  .
Например, орты
.
Например, орты 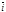 ,
,  ,
, 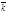 правой системы координат образуют правую тройку векторов. Векторным произведением двух векторов
правой системы координат образуют правую тройку векторов. Векторным произведением двух векторов 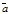 и
и 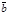 называется третий вектор
называется третий вектор 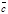 , обозначаемый символом
, обозначаемый символом 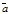 ´
´ 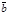 и удовлетворяющий условиям:
1.Модуль вектора
и удовлетворяющий условиям:
1.Модуль вектора 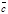 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах  и
и  т.е.,
т.е.,  , где j -угол между этими векторами.
2. Вектор
, где j -угол между этими векторами.
2. Вектор  ортогонален векторам
ортогонален векторам  и
и  .
3. Тройка векторов
.
3. Тройка векторов  ,
,  ,
,  правая.
Свойства векторного произведения.
1.
правая.
Свойства векторного произведения.
1. 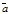 ´
´ 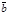 =-
=- 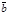 ´
´ 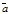 . Действительно, модуль векторного произведения
. Действительно, модуль векторного произведения 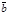 ´
´ 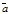 не меняется, т.к. численно равен площади параллелограмма, построенного на векторах
не меняется, т.к. численно равен площади параллелограмма, построенного на векторах  и
и  ; направление
; направление  ´
´  противоположно направлению
противоположно направлению  ´
´  , т.к. движение от вектора
, т.к. движение от вектора 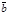 к вектору
к вектору  по меньшему углу с конца
по меньшему углу с конца  вектора -(
вектора -( ´
´  ) видно по направлению против часовой стрелки, (рис. 4).
2.
) видно по направлению против часовой стрелки, (рис. 4).
2.  ´
´  =
=  .
Указанное равенство следует из определения.
Замечание: Для того чтобы векторы были коллинеарны необходимо и достаточно, чтобы их векторное произведение было равно нуль вектору, т.е.
.
Указанное равенство следует из определения.
Замечание: Для того чтобы векторы были коллинеарны необходимо и достаточно, чтобы их векторное произведение было равно нуль вектору, т.е. 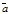 ´
´ 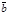 =
= 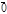 .
3.
.
3.  .
Докажем равенство
.
Докажем равенство  =
=  при l>0.
Пусть (
при l>0.
Пусть ( ´
´  )=
)=  и |
и |  |=abSinj. Тогда вектор
|=abSinj. Тогда вектор  имеем то же направление, что и вектор
имеем то же направление, что и вектор  . Но
. Но 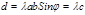 , значит
, значит 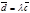 или
или 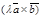 =
= 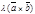 . Очевидно, что
. Очевидно, что  =
=  .
4.Для любых векторов
.
4.Для любых векторов  ,
, 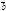 ,
,  имеет место равенство (
имеет место равенство ( +
+  )´
)´ 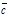 =
=  . Рассмотрим частный случай: пары векторов
. Рассмотрим частный случай: пары векторов 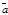 ,
,  и
и  ,
, 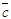 -правые. В этом случае векторы (
-правые. В этом случае векторы (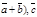 также образуют правую пару. Тогда векторы
также образуют правую пару. Тогда векторы  ,
, 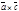 ,
,  коллинеарны и одинаково направлены. И нам остается доказать, что модуль вектора
коллинеарны и одинаково направлены. И нам остается доказать, что модуль вектора  равен сумме модулей векторов
равен сумме модулей векторов  и
и  , т.е. |
, т.е. | 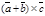 |=|
|=|  |+|
|+| 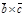 |.
Рассматривая соответствующие параллелограммы, (рис. 5), имеем
|.
Рассматривая соответствующие параллелограммы, (рис. 5), имеем  ,
,  .
.
 Так как
Так как  , то имеет место равенство площадей
, то имеет место равенство площадей

 . Откуда |
. Откуда | 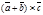 |=|
|=| 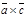 |+|
|+|  |, а значит
|, а значит
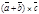 =
= 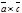 +
+ 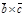 . Таким образом векторное произведение сумм векторов осуществляется
по правилу умножения многочленов.
5.Векторное произведение в координатах.
Пусть даны два вектора
. Таким образом векторное произведение сумм векторов осуществляется
по правилу умножения многочленов.
5.Векторное произведение в координатах.
Пусть даны два вектора 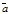 и
и 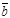 в координатах, т.е.
в координатах, т.е.
 ,
, 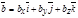 .
Тогда, используя свойства векторного произведения и условия
.
Тогда, используя свойства векторного произведения и условия
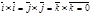 ,
, 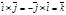 ,
,
 ,
, 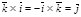 получим
получим  ´
´  =
= 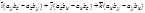 .
Или
.
Или 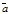 ´
´ 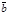 =
=  ,
откуда
,
откуда  ´
´  =
= 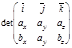 .
Замечание. Так как |
.
Замечание. Так как |  ´
´  |2 можно представить в виде
|
|2 можно представить в виде
|  ´
´  |2=
|2= 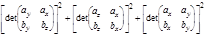 ,
то площадь S треугольника, построенного на векторах
,
то площадь S треугольника, построенного на векторах  и
и  можно вычислить по формуле S=1/2|
можно вычислить по формуле S=1/2|  ´
´  | или
| или
 , X={x| x³0}, Y={y| y³0}.
Способы задания функций
1. Аналитическое задание. Если указана совокупность операций, которые надо произвести над аргументом x, чтобы получить значение функции y, то говорят, что функция задана аналитически.
1). Явное задание: y=f(x).
Например, y=
, X={x| x³0}, Y={y| y³0}.
Способы задания функций
1. Аналитическое задание. Если указана совокупность операций, которые надо произвести над аргументом x, чтобы получить значение функции y, то говорят, что функция задана аналитически.
1). Явное задание: y=f(x).
Например, y=  +1, x³0; y=x2-5x-1.
2). Неявное задание: уравнение F(x,y)=0, при некоторых условиях, задает функцию y=f(x), если F(x, f(x))º0.
Например: Уравнение x2+y2=1 при y³0 задает функцию y=
+1, x³0; y=x2-5x-1.
2). Неявное задание: уравнение F(x,y)=0, при некоторых условиях, задает функцию y=f(x), если F(x, f(x))º0.
Например: Уравнение x2+y2=1 при y³0 задает функцию y= 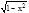 .
2. Табличное задание. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае получается таблица, в которой даются значения функции для конечного множества значений аргумента.
3. Графическое задание. Графиком функции y = f(x) называется геометрическое место точек плоскости OXY
вида M(x,f(x)), где x - произвольное
значение из области определения функции.
Указанное геометрическое место точек, как правило, образует некоторую кривую l.
В этом случае задание кривой l определяет отображение области определения на область изменения функции f(x) (см. Рис).
4. Словесное или описательное задание. В этом случае функциональная зависимость выражается некоторым словесным утверждением.
Например: Функция [x] есть целая часть числа x
Функция {x} есть дробная часть числа x
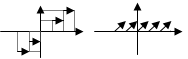
Графики функций y=[x] и y = {x} ºx-[x].
1. Заметим, что [x] означает целую часть числа x, т.е. [x]=n, если x=n+r, где 0£ r <1, причем данная функция определена при любом значении x из R.
Рассматривая промежутки изменения x вида n£x<n+1 при nÎZ, получим, что [x]=n. Поэтому нетрудно построить график y=[x].
2. Запишем выражение x-[ x ] на промежутке x Î [n; n + 1), тогда y=x-[x]=n+r-n=r. Следовательно, значение функции в точке n+r равно дробной части числа x, т.е. yÎ[0;1).
.
2. Табличное задание. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае получается таблица, в которой даются значения функции для конечного множества значений аргумента.
3. Графическое задание. Графиком функции y = f(x) называется геометрическое место точек плоскости OXY
вида M(x,f(x)), где x - произвольное
значение из области определения функции.
Указанное геометрическое место точек, как правило, образует некоторую кривую l.
В этом случае задание кривой l определяет отображение области определения на область изменения функции f(x) (см. Рис).
4. Словесное или описательное задание. В этом случае функциональная зависимость выражается некоторым словесным утверждением.
Например: Функция [x] есть целая часть числа x
Функция {x} есть дробная часть числа x
Графики функций y=[x] и y = {x} ºx-[x].
1. Заметим, что [x] означает целую часть числа x, т.е. [x]=n, если x=n+r, где 0£ r <1, причем данная функция определена при любом значении x из R.
Рассматривая промежутки изменения x вида n£x<n+1 при nÎZ, получим, что [x]=n. Поэтому нетрудно построить график y=[x].
2. Запишем выражение x-[ x ] на промежутке x Î [n; n + 1), тогда y=x-[x]=n+r-n=r. Следовательно, значение функции в точке n+r равно дробной части числа x, т.е. yÎ[0;1).
 |
Первый замечательный предел. 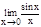 =1
=1
Рассмотрим тригонометрический круг. Имеем
|AC|=sin x
|BmC|=x
BD=tg x
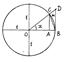 Очевидно, что sin x< x <tg x (при 0< x <p/2).
Очевидно, что sin x< x <tg x (при 0< x <p/2).
Разделим неравенство на sin x¹0, тогда
1< 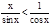 или 1>
или 1> 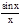 >cos x
>cos x
0>  -1>cos x-1; 0< 1-
-1>cos x-1; 0< 1-  <2sin2
<2sin2 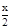 <2×
<2× 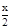 ×
×  =
= 
Так как 0 и 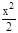 есть бесконечно малые функции при х®0, то и 1-
есть бесконечно малые функции при х®0, то и 1-  при õ®0 бесконечно малая функции. Значит
при õ®0 бесконечно малая функции. Значит 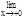
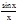 =1.
=1.
Замечание. Доказательство проведено для х>0. Однако, если х<0, то под знаком предела можно сделать замену х=-t, t®+0: 
 =
= 
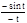 =
= 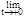
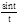 =1.
=1.
Следовательно  =1
=1
Признаки существования предела
1. Если и  , то
, то

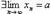
2. Монотонная и ограниченная последовательность имеет предел.
3. Числовая последовательность (xn) имеет конечный предел тогда и только тогда, когда 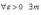



 Это свойство можно строго сформулировать математически и оно имеет большое значение в математике.
Определение предела (по Коши). Функция f(x) хÎХ имеет своим пределом число А при стремлении x к предельной точке х0 множества Х, если для каждого числа e>0 существует число d(e)>0 такое, что при всех х из окрестности |x-x0|<d, x¹x0 имеет место неравенство |f(x)-A|<e.
Символически этот факт записывают в виде
Это свойство можно строго сформулировать математически и оно имеет большое значение в математике.
Определение предела (по Коши). Функция f(x) хÎХ имеет своим пределом число А при стремлении x к предельной точке х0 множества Х, если для каждого числа e>0 существует число d(e)>0 такое, что при всех х из окрестности |x-x0|<d, x¹x0 имеет место неравенство |f(x)-A|<e.
Символически этот факт записывают в виде 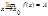 .
Геометрическая интерпретация.
.
Геометрическая интерпретация.
 Если функция у=f(x) хÎХ имеет своим пределом число А при х®х0, то разность значений функции и ее предела А достаточно мала, если значение аргумента х близко к х0.
Геометрически это означает, что график функции y=f(x) виден в «окошке» плоскости OXY c координатами: хÎ(х0-d; х0+d), х¹х0, d=min(d1, d2); yÎ(A-e; A+e), А - предел функции, e - любое положительное число.
Особо отметим, что график функции может «выйти» из указанного «окошка» только через боковые стороны. Только через них!
Отметим еще одну особенность: при рассмотрении предела функции в точке х0 само значение функции в точке х0 исследователя не интересует. Это значение f(x0) может быть, в общем случае, равным А или не равным А, или, наконец, функция f(x) в точке х0 может быть не определена.
Определение предела (по Гейне). Функция f(x) хÎХ имеет своим пределом число А при стремлении х к предельной точке х0, если для любой последовательности xn сходящейся к х0, причем xn¹х0 (xnÎ X) последовательность f(xn) сходится к А.
Символическая запись.
Если функция у=f(x) хÎХ имеет своим пределом число А при х®х0, то разность значений функции и ее предела А достаточно мала, если значение аргумента х близко к х0.
Геометрически это означает, что график функции y=f(x) виден в «окошке» плоскости OXY c координатами: хÎ(х0-d; х0+d), х¹х0, d=min(d1, d2); yÎ(A-e; A+e), А - предел функции, e - любое положительное число.
Особо отметим, что график функции может «выйти» из указанного «окошка» только через боковые стороны. Только через них!
Отметим еще одну особенность: при рассмотрении предела функции в точке х0 само значение функции в точке х0 исследователя не интересует. Это значение f(x0) может быть, в общем случае, равным А или не равным А, или, наконец, функция f(x) в точке х0 может быть не определена.
Определение предела (по Гейне). Функция f(x) хÎХ имеет своим пределом число А при стремлении х к предельной точке х0, если для любой последовательности xn сходящейся к х0, причем xn¹х0 (xnÎ X) последовательность f(xn) сходится к А.
Символическая запись.  :
1. По Коши: для " e>0, $ d(e, x0)>0, что при |x-x0|<d(e), x¹x0 => |f(x)-A|<e.
2. По Гейне: для " xn®x0, xn¹x0 => f(xn)®A.
Отметим, что определения предела функции в точке по Коши и по Гейне -
эквивалентны.
Сформулируем далее следующие утверждение: число А не является пределом функции f(x) в точке х=х0.
Данное утверждение обычно называют отрицанием предела.
Отрицание предела.
:
1. По Коши: для " e>0, $ d(e, x0)>0, что при |x-x0|<d(e), x¹x0 => |f(x)-A|<e.
2. По Гейне: для " xn®x0, xn¹x0 => f(xn)®A.
Отметим, что определения предела функции в точке по Коши и по Гейне -
эквивалентны.
Сформулируем далее следующие утверждение: число А не является пределом функции f(x) в точке х=х0.
Данное утверждение обычно называют отрицанием предела.
Отрицание предела.  ¹А.
По Коши: $ e0>0 такое, что для " d>0 существует точка х*ÎХ такая, что |x*-x0|<d, x*¹x0, но |f(x*)-A|³e0.
По Гейне: $ xn*®x0, xn*¹x0, что f(xn*) / A.
¹А.
По Коши: $ e0>0 такое, что для " d>0 существует точка х*ÎХ такая, что |x*-x0|<d, x*¹x0, но |f(x*)-A|³e0.
По Гейне: $ xn*®x0, xn*¹x0, что f(xn*) / A.
 и
и  .
1.Одна и та же функция в одной и той же точке может иметь только один предел.
.
1.Одна и та же функция в одной и той же точке может иметь только один предел.  2.Сходящаяся функция локально сохраняет знак. Более обще,
2.Сходящаяся функция локально сохраняет знак. Более обще, 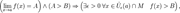 где
где  — проколотая окрестность точки a.
3.В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
— проколотая окрестность точки a.
3.В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки: 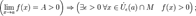 4.Сходящаяся функция локально ограничена в окрестности предельной точки:
4.Сходящаяся функция локально ограничена в окрестности предельной точки: 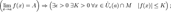 5.Отделимость от нуля функций, имеющих предел, отличный от нуля.
5.Отделимость от нуля функций, имеющих предел, отличный от нуля.  6.Операция взятия предела сохраняет нестрогие неравенства.
6.Операция взятия предела сохраняет нестрогие неравенства.  7. Предел суммы равен сумме пределов:
7. Предел суммы равен сумме пределов:  8. Предел разности равен разности пределов:
8. Предел разности равен разности пределов: 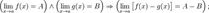 9. Предел произведения равен произведению пределов:
9. Предел произведения равен произведению пределов:  10. Предел частного равен частному пределов.
10. Предел частного равен частному пределов. 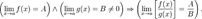 Второй замечательный предел.
Второй замечательный предел. 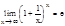 Мы уже встречались ранее с пределом
Мы уже встречались ранее с пределом  (1+1/n)n=e при nÎN. Очевидно
(1+1/n)n=e при nÎN. Очевидно 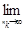 (1+1/nk)nk=e, при nkÎN, т.к. последовательность (1+1/nk)nkявляется подпоследовательностью сходящейся к е, последовательности (1+1/n)n.
Возьмем далее произвольную последовательность хк сходящуюся к +¥, т.е. хк®+¥, при к®¥.
Тогда имеем nk£xk<nk+1, где nk=[xk], а также
(1+1/nk)nk=e, при nkÎN, т.к. последовательность (1+1/nk)nkявляется подпоследовательностью сходящейся к е, последовательности (1+1/n)n.
Возьмем далее произвольную последовательность хк сходящуюся к +¥, т.е. хк®+¥, при к®¥.
Тогда имеем nk£xk<nk+1, где nk=[xk], а также  ;
; 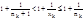 ;
;  .
То есть
.
То есть 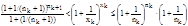 . Пределы левой и правой частей при к®¥ равны е, т.к. nk®+¥ (очевидно и хк®+¥) и
. Пределы левой и правой частей при к®¥ равны е, т.к. nk®+¥ (очевидно и хк®+¥) и  (1+1/nk)nk=e. Откуда по теореме о зажатой последовательности имеем
(1+1/nk)nk=e. Откуда по теореме о зажатой последовательности имеем
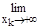 (1+1/хk)хk=e при хк®+¥.
Тогда по определению предела по Гейне получаем, что
(1+1/хk)хk=e при хк®+¥.
Тогда по определению предела по Гейне получаем, что
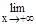 (1+1/х)х=e - 2ойзамечательный предел.
Имеет место также равенство
(1+1/х)х=e - 2ойзамечательный предел.
Имеет место также равенство  (1+1/х)х=e т.к. сделав замену -х=t, получим:
(1+1/х)х=e т.к. сделав замену -х=t, получим:  (1-1/t)-t=
(1-1/t)-t= 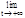
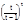 =
= 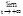
 =
= 
 = e
= e
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 335; Нарушение авторских прав?; Мы поможем в написании вашей работы!