Тема: Фазовые переходы. Диаграмма состояний. Особенности жидкого состояния вещества. Поверхностное натяжение. Давление под искривленной поверхностью жидкости. Капиллярные явления

Лекция № 18.

Фазой называется физически однородная часть вещества, отделенная от других частей системы границей раздела. Различают фазовые переходы 1-го и 2-го рода. Первые сопровождаются теплотой перехода. Это то ко­личество теплоты, которое необходимо сообщить веществу, что­бы изотермически–изобарически перевести его из одной фазы в другую. Этот процесс характеризуют удельной теплотой испарения (конденсации) 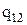, Дж/кг и удельной теплотой плавления (кристаллизации) 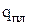, Дж/кг. Теплоту испарения твердого тела называют теплотой сублимации. Фазовые переходы 2-го рода происходят без теплообмена.

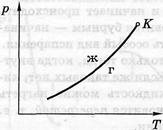
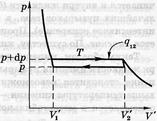Известно, что две лю­бые фазы вещества могут находиться в равновесии лишь при определенном давлении, зависящем от температуры. Для испарения (конденсации) кривая зависимости р(Т) по­казана на рисунке, где К – критическая точка, слева от этой кривой – жидкая фаза, справа – газообразная. Её называют кривой равновесия жидкости и её насыщенного пара или кривой испарения. Определим наклон кривой 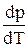. Для этого рассмотрим цикл Карно в области фазового перехода. 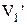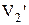и – удельные объемы фазы 1 и фазы 2, т.е. объемы единицы массы. При изобарическом расширении газ совершил работу:

.

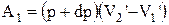Работа изобарического сжатия производится при более низкой температуре и определяется по формуле:

.

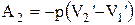Работой при адиабатическом расширении и сжатии будем пренебрегать по причине малости участков. Полная работа за цикл равна:

.

C другой стороны работу газа за цикл можно найти как 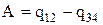, где 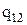– удельная теплота парообразования на участке 1-2, 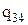– удельная теплота парообразования на участке 3-4, Так как 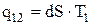, а 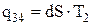, то после подстановки получаем: 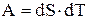. Таким образом:

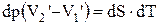и .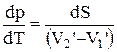

Учитывая, что 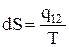, окончательно имеем:

.

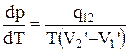Полученное уравнение называется уравнением Клапейрона–Клаузиуса. Видно, что знак производной, характеризующей наклон кривой р(Т), зависит от того, как изменяются удельные объе­мы при поглощении тепла – возрастают или уменьшаются. При испарении жидкости или твердого тела удельный объем всегда возрастает, поэтому производная dp/dT соответствую­щих кривых может быть только положительной. Следует заметить, что кривая испарения твердого тела называется кривой сублимации. При плавлении удельный объем подавляющего числа ве­ществ возрастает, поэтому dp/dT > 0. Однако у некоторых ве­ществ, к числу которых принадлежит вода, объем жидкой фазы меньше объема твердой фазы, и dp/dT < 0.

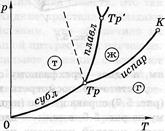Диаграммой состояний называют плоскость р, Т, разделенную на три области: твер­дую фазу (т), жидкую (ж) и газооб­разную (г). Границами этих соприкасающихся фаз являются кривые сублимации, испарения и плавле­ния, характеризующие двухфаз­ные равновесные состояния. В точ­ке Т_Р, называемой тройной, в равновесии находятся три фазы. Польза диаграммы состояний заключается в том, что она позволяют предсказывать фазовые превращения в тех или иных процессах.

Дата добавления: 2014-11-20