Величины в заданный интервал

Вероятность попадания непрерывной случайной

Дифференциальная функция распределения

Распределения для дискретной случайной величины

График интегральной функции

График интегральной функции для дискретной случайной величины прерывный, ступенчатый.

вероятностей (функция плотности)

Определение. Дифференциальной функцией ѓ(х) распределения случайной величины Х называется первая производная от её интегральной функции:

ѓ(х) = F' (x).

Замечание 1. Из определения ѓ(х) видно, что F(x) – первообразная для ѓ(х)

Замечание 2. Так как функция F(x) для дискретной случайной величины разрывна, то для описания распределения дискретной случайной величины дифференциальная функция не применима.

Таким образом, в отличие от интегральной функции распределения форма распределения вероятностей с помощью дифференциальной функции не является универсальной; она существует только для непрерывных случайных величин.

График дифференциальной функции ѓ(х) называется кривой распределения.

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, в), равна определённому интервалу от дифференциальной функции, взятому в пределах от а до в

.

Геометрически это можно истолковать так: Р(а < Х < в) численно равна площади криволинейной трапеции, ограниченной линиями:

х=а, х=в, у=0, у= ƒ(х).

Замечание: если ѓ(х) чётная, концы интервала симметричны относительно начала координат, то

Зная дифференциальную функцию, можно найти интегральную функцию распределения вероятностей по формуле:

.

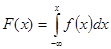Дата добавления: 2014-11-20