Основные сведения из теории. 1. По результатам лабораторной работы определить радиус кривизны контролируемой ППП

Контрольные вопросы

1. По результатам лабораторной работы определить радиус кривизны контролируемой ППП.

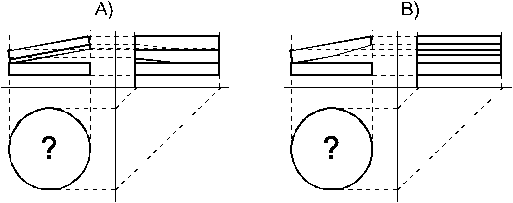
2. Как будет выглядеть интерференционная картина в клине, образованном плоской пластинкой, и пластинки, в форме двухгранного угла (рис. 1.8А)? Если пластинку развернуть на 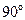(рис. 1.8В)?

Рис.1. 8

3. Как будет выглядеть интерференционная картина в клине, образованном ППП и пластинкой в виде конуса?

4. Свет с 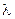=0.55 мкм падает нормально на поверхность стеклянного клина. Определить угол между гранями клина 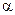, если расстояние между полосами 0.21 мм, а показатель преломления стекла 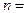1.5?

5. Обосновать метод определения выпуклости или вогнутости испытуемой пластинки.

2. Лабораторная работа “Интерферометр Майкельсона”

Целью работы является ознакомление с интерференцией световых пучков и нахождения информации о волновых фронтах по интерференционной картине.

Название “интерферометр Майкельсона” объединяет большую группу интерферометров, решающих различные задачи, но использующих в своей основе одну и ту же принципиальную схему, которая выглядит следующим образом (рис 2.1).

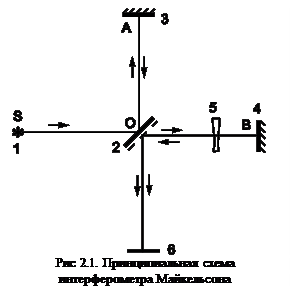Пучок света от источника (1), попадая на светоделитель (2), расщепляется на две ветви OA и OB. Отражатели (3) и (4) возвращают пучки на светоделитель (2), где они объединяются и образуют интерференционную картину на экране (6). В одной из ветвей интерферометра, в данном случае в OB (ветви совершенно равноправны), расположен фазовый объект (5). Фазовый объект это условное название. Им может быть, например, кювета с исследуемой жидкостью или газом, образец оптического стекла с неким неравномерным распределением показателя преломления или, наконец, фазовую неоднородность может содержать один или оба отражателя (к примеру, деформированное зеркало). В любом случае влияние неоднородности вызовет изменение фазы в одной или двух ветвях интерферометра, что математически означает появление в выражении для комплексной амплитуды множителя 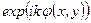, где 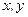- координаты в плоскостях, перпендикулярных направлениям распространения пучков. Обнаружить фазу 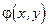можно лишь только с помощью интерференции, поскольку ее непосредственное определение невозможно. Действительно, любой детектор светового излучения реагирует только на энергию излучения, т.е. выполняет операцию

,

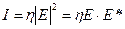(2.1)

где 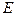- распределение комплексных амплитуд исследуемого светового потока, 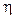- некий коэффициент, зависящий от вида детектора. Применяя эту операцию к световому полю с фазой 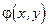, получим

,

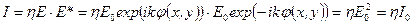(2.2)

где 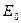- амплитуда напряженности электрического поля световой волны, 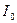- распределение освещенности на поверхности детектора. Таким образом, информация о фазе бесследно исчезает.

В случае же интерференции двух пучков информация о фазе может быть получена. Действительно, в этом случае

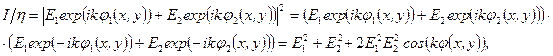
(2.3)

где 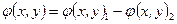- разность фаз ветвей. (При выводе была использована формула Эйлера 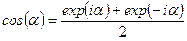). В плоскости анализа образуется распределение освещенности 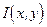, которое представляет собой некоторую периодическую структуру, благодаря наличию в выражении функции 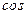содержит информацию о фазе. Эту информацию проще всего получить, исследуя 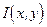на максимумы и минимумы. Действительно, максимум 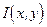достигается при 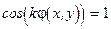, а минимум - когда 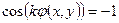. Таким образом, решая тригонометрическое уравнение 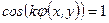для максимумов 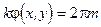, и учитывая, что 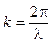, получим

.

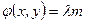(2.4а)

Для минимумов, соответственно

.

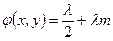(2.4б)

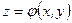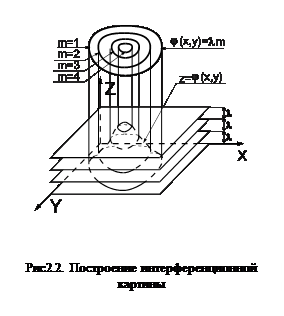
Выражения (2.4а.) и (2.4б) представляют собой сечения функции плоскостями, параллельными плоскости OXY и отстоящими друг от друга на расстояниях 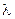, т.е. интерференционная картина как бы представляет собой географическую карту поверхности (рис 2.2), заданную уравнением 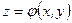, при этом светлые полосы соответствуют максимумам, а темные - минимумам. Расшифровка такой интерференционной картины обычно не представляет труда, однако надо помнить, что в интерференционной картине не содержится информации о выпуклости или вогнутости функции 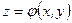, эта информация должна быть получена из других источников.

Дата добавления: 2014-12-08