Энергия системы зарядов

Конденсаторы

При поднесении к заряженному проводнику какого-либо тела потенциал проводника уменьшается по абсолютной величине, вследствие возникновения индуцированных (на проводнике) или связанных (на диэлектрике) зарядов. Это явление положено в основу устройств, называемых конденсаторами. Найдем формулу для емкости плоского конденсатора. Если площадь обкладки S, а заряд на ней q, то напряженность поля между обкладками равна:

.

Разность потенциалов между обкладками равна:

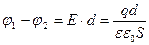, откуда для емкости плоского конденсатора получаем:

,

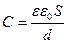где d – величина зазора между обкладками.

Пусть имеются заряды q ₁ и q ₂, находящиеся на расстоянии r ₁₂. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сближение зарядов можно произвести приближая q ₁ к q ₂, либо наоборот. В обоих случаях совершается одинаковая работа. Работа переноса заряда q ₁ из бесконечности в точку, удаленную от q ₂ на r ₁₂, равна:

, (19)

где 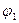- потенциал, создаваемый зарядом q ₂ в той точке, в которую перемещается заряд q ₁. Аналогично работа переноса заряда q ₂ из бесконечности в точку, удаленную от q ₁ на r ₁₂, равна:

, (20)

где - потенциал, создаваемый зарядом q₁ в той точке, в которую перемещается заряд q₂. Значения работ (19) и (20) одинаковы, и каждое из них выражает энергию системы:

.

Для того чтобы в выражении энергии системы оба заряда входили симметрично, напишем его следующим образом:

. (21)

В случае N зарядов потенциальная энергия системы равна:

, (22)

где - потенциал, создаваемый в той точке, где находится q_i, всеми зарядами, кроме i -го.Процесс возникновения на обкладках конденсатора зарядов +q и –q можно представить так, что от одной обкладки последовательно отнимаются порции заряда и перемещаются на другую обкладку. Работа переноса очередной порции равна:

,

где U – напряжение на конденсаторе. Заменяя U через отношение заряда к емкости и переходя к дифференциалам, получим:

.

Интегрируя, получим:

.

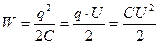Энергию конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это для плоского конденсатора. Подставим в выражение для энергии конденсатора выражения для емкости плоского конденсатора, тогда:

. (23)

Так как , а S·d=V – объем, занимаемый полем, то можно написать:

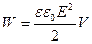. (24)

Формула (23) связывает энергию конденсатора с зарядом на его обкладках, формула (24) – с напряженностью поля. Логично поставить вопрос: где же локализована (т.е. сосредоточена) энергия, что является носителем энергии – заряды или поле? В пределах электростатики, изучающей постоянные во времени поля неподвижных зарядов, дать ответ на этот вопрос невозможно. Постоянные поля и обусловившие их заряды не могут существовать обособленно друг от друга. Однако меняющиеся во времени поля могут существовать независимо от возбудивших их зарядов и распространяться в пространстве в виде электромагнитных волн. Опыт показывает, что электромагнитные волны переносят энергию. Следовательно, носителем энергии является поле.

Если поле однородно, заключенная в нем энергия распределяется в пространстве с постоянной плотностью равной энергии поля, деленной на заполняемый полем объем. Следовательно, плотность энергии поля плоского конденсатора:

.

Этой формуле можно придать вид:

,

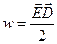заменив D (14), получим плотность энергии в диэлектрике:

.

Первое слагаемое совпадает с плотностью энергии поля в вакууме. Второе – представляет собой энергию, затрачиваемую на поляризацию диэлектрика.

Дата добавления: 2014-12-08