
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Практична робота №1
Визначення координат точок об’єкта (місцевості) при відомих елементах зовнішнього орієнтування поодинокого кадрового аерофотознімка
Мета роботи: поглиблення і закріплення теоретичних знань з курсу за темою: «Метричні властивості та використання поодинокого аерофотознімка» та набуття практичних навиків з визначення координат точок об’єкта при розв’язанні прямої фотограмметричної засічки та через трансформовані координати.
На виконання роботи відводиться 6 год. (2 год. на виконання домашнього завдання та підготовки до виконання роботи та 4 год. аудиторної роботи).
До виконання роботи допускаються студенти, які опрацювали теоретичний матеріал за даною темою та дали письмові відповіді на контрольні питання та завдання.
1. Послідовність виконання роботи
1. Опрацювати теоретичний матеріал за наступними літературними джерелами: [1, с.22-38; 2, с.29-39;51-53; 3, с.29-40; 4, розділ ІІ «Метричні властивості поодинокого кадрового аерофотознімка»].
2. Дати відповіді на контрольні питання та завдання.
3. Виконати аудиторне завдання у відповідності із змістом.
1.1. Список рекомендованої літератури
- Дорожинський О.Л. Основи фотограмметрії.: Підручник.-Львів: Видавництво НУ «Львівська політехніка», 2003.-214с.
- Рудий Р.М. Прикладна фотограмметрія: Навч.посібник. – К.: НМК ВО, 1991.-169с.
- Лобанов А.Н., Буров М. И., Краснопевцев Б.В. Фотограмметрия: Учебник для вузов. – М.: Недра,1987.-309с.
- Процик М.Т. Фотограмметрія та дистанційне зондування: Конспект лекцій [текст].
2. Контрольні запитання та завдання
(для виконання домашньої роботи)
- Що таке елементи внутрішнього орієнтування знімка? Що вони визначають? Зарисуйте схему елементів внутрішнього орієнтування.
- Які фотограмметричні дані є елементами зовнішнього орієнтування поодинокого знімка? Що вони визначають? Скільки елементів зовнішнього орієнтування?
- Перечисліть елементи зовнішнього орієнтування першої і другої системи і зобразіть дані величини на рисунках.
- Що таке напрямні косинуси? Запишіть формули для визначення матриці напрямних косинусів для двох систем.
- Запишіть матриці напрямних косинусів для випадків, коли два кутових елементи дорівнюють 0, а третій не дорівнює 0, для двох систем.
- Скільки координат точок об’єкта визначається за даними поодинокого знімка? Які?
- В якому випадку можна побудувати модель об’єкта за його зображеннями на поодинокому знімку? Якою буде ця модель?
- Які фотограмметричні дані необхідно знати для виконання аналітичного трансформування аерофотознімка?
- Чи потрібно знати лінійні елементи зовнішнього орієнтування при перетворенні похилого знімка до горизонтального? Чому?
3. Короткі теоретичні відомості
Положення знімка в просторі в момент фотографування в декартовій зовнішній координатній системі (системі координат об’єкта) однозначно визначається 6 параметрами – елементами зовнішнього орієнтування. Положення знімка відносно центра фотографування S визначають елементи внутрішнього орієнтування {xo, yo, f }, які дозволяють встановити зв'язку проектуючих променів в момент фотографування. Оскільки зв'язка побудована в системі координат знімка o'xyz то ці параметри є параметрами зв’язку двох просторових систем координат OXYZ і Sxyz (рис.1).
Таким чином, для орієнтування системи координат знімка відносно системи координат об’єкта необхідно знати шість елементів зовнішнього орієнтування.

Рис.1.
На рис.1 показана система координат об’єкта OXYZ, система координат знімка o'xy та допоміжні координатні системи з початком в точці S: Sxyz-координатні осі якої є паралельними до координатних систем знімка, а вісь z направлена по головному оптичному променю So і SX'Y'Z' координатні осі паралельні відповідним осям системи координат об’єкта OXYZ. Вектор 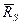 {Xs, Ys, Zs} визначає положення проекції S в системі координат об’єкта, вектор
{Xs, Ys, Zs} визначає положення проекції S в системі координат об’єкта, вектор  {X, Y, Z} визначає положення точки М в системі координат об’єкта, а вектор R'{X', Y', Z'} – положення точки m в допоміжній системі координат SX'Y'Z'. Положення на знімку зображення m точки об’єкта М визначає вектор rm{x, y, z= -f } в системі координат знімка Sxyz.
{X, Y, Z} визначає положення точки М в системі координат об’єкта, а вектор R'{X', Y', Z'} – положення точки m в допоміжній системі координат SX'Y'Z'. Положення на знімку зображення m точки об’єкта М визначає вектор rm{x, y, z= -f } в системі координат знімка Sxyz.
Елементами зовнішнього орієнтування знімка (I – система) є координати XsYsZs центра проекції S в системі координат об’єкта OXYZ і кути повороту α, ω, χ системи координат знімка Sxyz відносно координатної системи об’єкта OXYZ (SX'Y'Z').
Кут повороту ω називається поперечним (тангаж для літака) і визначає поворот навколо осі Sx, кут повороту α називається повздовжнім (крен) і визначає поворот навколо осі Sy, кут χ називається кутом розвороту (знос) і означає поворот навкруг осі Sz.
Координати точки об’єкта і їх зображення на знімку зв’язані векторним рівнянням, яке називають рівнянням колінеарності:
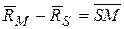
| (1) |
Вектори 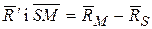 колінеарні, тому:
колінеарні, тому:
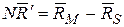
| (2) |
або в координатній формі:
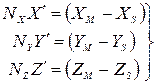
| (3) |
звідси:
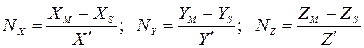
| (4) |
де N – скаляр, або масштабний множник. Підставивши останню рівність з (4) в два перших рівняння (3), маємо:
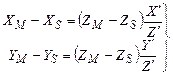 або або 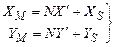
| (5) |
де: XM, YM, ZM – координати точки М в системі координат об’єкта;
XS, YS, ZS – координати центра проекції S в системі координат об’єкта;
X', Y', Z' – координати точки в допоміжній системі координат SX'Y'Z'.
Зазвичай на знімку вимірюють плоскі прямокутні координати x', y' в системі координат o'xy, або переходячи до допоміжної просторової системи координат знімка Sxyz точка m буде визначатися вектором:
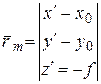
| (6) |
де: x', y' – виміряні координати точки m на знімку в системі координат o'xy;
x0, y0, f – елементи внутрішнього орієнтування, які визначають положення головної точки «о» на знімку відносно системи координат знімка.
Для визначення координат X'Y'Z' точок знімка в координатній системі SX'Y'Z' за відомими координатами точок знімка x', y', - f в системі координат Sxyz використовують відоме в математиці перетворення координатних систем (простору):
 , ,
| (7) |
де 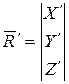 - результуючий вектор;
- результуючий вектор;
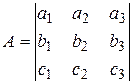
| (8) |
(ai, bi, ci)i=1÷3 – елементи матриці, напрямні косинуси;
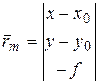 - вхідний вектор
- вхідний вектор
або в координатній формі
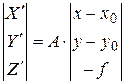 , ,
| (9) |
або,
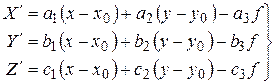 , ,
| (10) |
Таким чином, якщо відомі елементи зовнішнього орієнтування α, ω, χ (α', t, χ'), Xs, Ys, Zs і висоти точок Zі, то за формулами (5) можна визначити координати точок об’єкта X,Y.
Елементи зовнішнього орієнтування можуть бути визначені в результаті фотограмметричного опрацювання знімків за опорними точками, або отримані під час знімання за даними опрацювання бортових супутникових кінематичних вимірювань і вимірювання інерційної системи.
Матрицю напрямних косинусів (8) обчислюють за формулами:
| I система | II система |
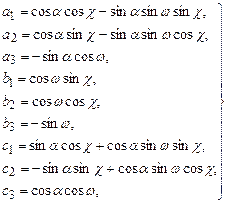
| 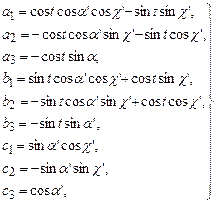 (11) (11)
|
Якщо відомі напрямні косинуси, то можна визначити кутові елементи зовнішнього орієнтування. Для прикладу в I-системі вони визначають так:
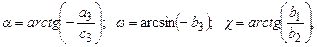
|
Формули (5) справедливі для довільних кутових елементів зовнішнього орієнтування.
Для планового знімка кутові елементи зовнішнього орієнтування знімка є малими величинами. Тому тригонометричні функції кутів α, ω і χ можна розкласти в ряди і зберегти при цьому члени першого і другого порядку малості отримати такі формули:
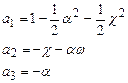 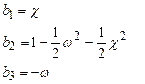 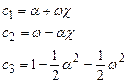
| (12) |
Для випадку аерознімання із використанням гіростабілізаційної установки кутові елементи, як правило, не перевищують 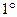 , тоді матрицю напрямних косинусів можна представити тільки членами першого порядку малості, а саме:
, тоді матрицю напрямних косинусів можна представити тільки членами першого порядку малості, а саме:
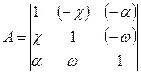
| (13) |
Для горизонтального знімка (α=ω=χ=0) матриця А перетвориться в одиничну матрицю:
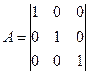
| (14) |
Формули (1)-(14) є теоретичним обґрунтуванням розв’язання прямої фотограмметричної засічки для поодинокого кадрового аерофотознімка.
Другий шлях отримання планових координат точок об’єкта (місцевості) пов'язаний з використанням формул аналітичного трансформування.
Як відомо, кадровий аерофотознімок представляє собою зображення точок земної поверхні на площині, зафіксованих в один момент часу в перспективній центральній проекції. Такий знімок має кути нахилу відносно прямовисної лінії до поверхні референц-еліпсоїда, що приводить до зміщення точок на знімку по відношенню до їх положення на горизонтальному знімку. Такі зміщення підчиняються певному закону і, якщо відомі кути нахилу знімка, то вони легко враховуються при переході із системи координат знімка до системи координат місцевості.
Процес перетворення координат похилого аерознімка в координати горизонтального знімка в задану проекцію відповідного масштабу називається трансформуванням знімків.
В деяких випадках при розв’язанні фотограмметричних задач нема необхідності переходу до заданої проекції і приведення знімків до заданого масштабу, а достатньо отримати трансформовані координати за виміряними координатами похилого знімка. Для цього використовують просторову координатну систему знімка з початком в точці фотографування S і приймають що похилий і горизонтальний знімок отримані з однієї точки фотографування. Геометрична інтерпретація показана на рис.2.
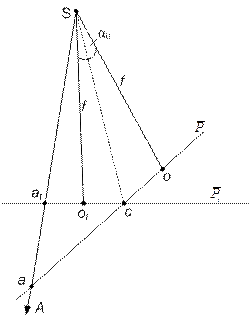 Рис.2.
Рис.2.
Розрахунки виконуються за наступними формулами:

| (15) |
де { x0, y0, f } – елементи внутрішнього орієнтування аерознімків;
{ ai, bi, ci }i=1-3 – напрямні косинуси обчислені за кутовими елементами зовнішнього орієнтування аерофотознімка α, ω, χ (α', t', ω').
Залежності (15) є рівняннями аналітичного трансформування загального вигляду і справедливі для довільних значень кутових елементів зовнішнього орієнтування.
Для планових та гіростабілізованих аерофотознімків існують наближені формули трансформування такого вигляду:
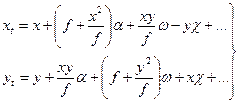
| (16) |
4. Вхідні дані і матеріали:
- поодинокі кадрові аерофотознімки;
- елементи внутрішнього орієнтування;
- елементи зовнішнього орієнтування.
XS=1000м; YS=1000м; ZS= Hабс; x0= мм; y0= мм; f= мм;
Таблиця 1
| Характеристика знімків | α° | ω° | κ° |
| перспективний | |||
| плановий | |||
| гіростабілізований | |||
| горизонтальний | 0 ° | 0 ° | 0 ° |
Z1= м; Z2= м; Z3= м; Z4= м; Hабс= м.
Примітка: вхідні дані видаються кожному студенту індивідуально
|
|
Дата добавления: 2014-12-08; Просмотров: 2079; Нарушение авторских прав?; Мы поможем в написании вашей работы!