Связь линейных отображений с матрицами. 1 страница

Пусть дано линейное отображение L линейного пространства V₁ в линейное пространство V_2. Пусть 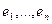- базис V₁, а 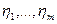- базис V_2. Для любого х из V₁ имеем: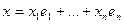

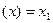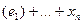L L L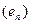

Пусть L ,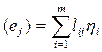

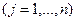
Тогда L .

Введем матрицу L

3)

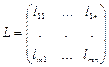
Тогда координаты вектора L (х) можно вычислить по формуле:

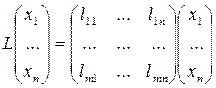
Определение 13. Матрица, определенная равенством (3), называется матрицей линейного отображения L в базисах ; .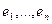

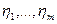Обратно. Если есть некая матрица:

и два пространства: V₁ c базисом 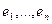и V₂ с базисом 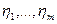, то можно задать линейное отображение L формулами:

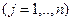
L ,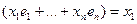

L L 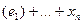L L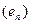

Замечание. Рангом матрицы называют наибольший порядок минора матрицы, отличного от нуля. Можно показать, что ранг матрицы равен рангу линейного отображения. А именно изменяя базисы в пространствах V₁ и V₂ мы все сведем к случаю матрицы вида:

,

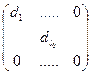Где на пустых местах стоят нули. Заметив, что dim{ im L ,b} равна рангу матрицы:

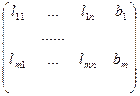, получим теорему (теорема Крокенера-Капелли): чтобы система:

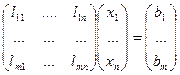
Имела решение, необходимо и достаточно, чтобы ранг матрицы 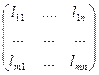был равен рангу матрицы .

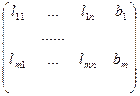§ 4. Композиция линейных отображений.

Пусть даны линейные пространства V₁, V₂, V₃ и линейные отображения L₁: V₁→V₂; L₂: V₂→V₃. Рассмотрим отображение L₃: V₁→V₃, определенное формулой: для любого х из V₁: L₃ L_{2 (} L₁ (х))

Утверждение. L_{3 –} линейное отображение.

Доказательство. Пусть V₁, V₂ V₁ и α, β – любые числа.

L₃ 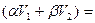L_{2 (} L₁ 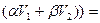L₂₍ α 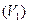L₁ +β L₁ 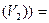α L₂₍L₁ 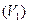)+β L₂₍L₁ 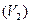)=α 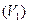L₃ +β L₃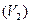

Теорема 4. В обозначениях, введенных выше: dim ker L₃ = dim ker L₁ +dim(ker L₂ im L₁)

Доказательство. Пусть а₁, …, а_r – базис пространства ker L₂ im L₁ и V₁, …, V_r – такие вектора из V₁, что L₁ 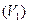=а₁, …, L₁ 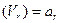. Пусть e₁,…,e_S – базис подпространства ker L₁. Покажем, что V₁, …, V_r, e₁,…,e_S линейно независимы. Пусть числа 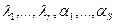таковы, что: .

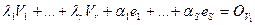Применим к этому равенству отображение L₁ . Тогда получим:

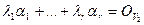, и так как а₁, …, а_r – базис, то 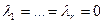. Отсюда:

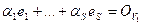, и, следовательно, 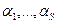=0. Итак V₁, …, V_r, e₁,…,e_S линейно независимы. Пусть теперь 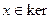L₃. Тогда L_{2 (} L₁ (х))= L₃ (х)= 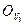. Следовательно, L₁ (х) ker L₂ im L₁. Поэтому существуют такие числа 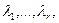что:

L₁ (х)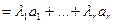

Рассмотрим вектор 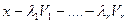. Имеем:

L₁ ( )= L₁ (х)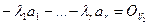

Поэтому 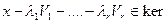L₁. Отсюда получаем:

.

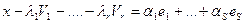Окончательно:

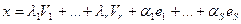
То есть V₁, …, V_r, e₁,…,e_S базис ker L₃. Так как S =dim ker L₁, r =dim(ker L₂ im L₁), то:

dim ker L₃ =dim ker L₁ +dim(ker L₂ im L₁) и теорема доказана.

Матрица композиции. Пусть в V₁, V₂, V₃ зафиксированы базисы 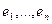, , 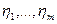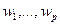. И в этих базисах отображению L₁ соответствует матрица:

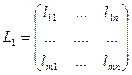
А отражению L₂ соответствует матрица:

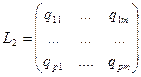
Тогда мы имеем: L₃ (e_j) = L_{2 (} L₁ (e_j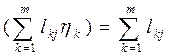))= L₂ L₂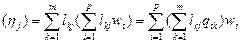

Из правил умножения матриц следует, что отображению L₃ = L₂ ◦ L₁ соответствует матрица:

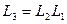
Исследуем теперь, что происходит с матрицей линейного отображения при изменении базиса. Пусть дано линейное пространство V, и в нем два базиса: 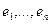и 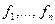. Возьмем произвольный вектор х и рассмотрим его координаты в этих базисах. Найдем, как они связаны. Для этого обозначим I_V – тождественное отображение пространства V. То есть:

для любого х из V. Имеем:

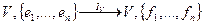
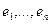Пусть P – матрица отображения в базисах и 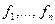. По доказанному выше, если 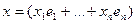, то его координаты в базисе 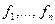(так как ) находятся по формуле:

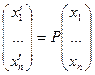
Матрица Р называется матрицей перехода от базиса 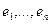к базису .

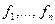Рассмотрим теперь более общую ситуацию:

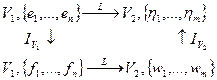
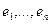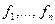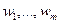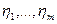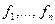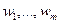Пусть Р – матрица перехода от базиса к базису ; Q – матрица перехода от базиса к базису . Далее, пусть L – матрица, соответствующая отображению L в базисах и , а 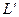- матрица, соответствующая отображению L в базисах 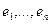и 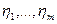. По формуле для матрицы композиции линейных отображений имеем:

.

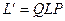Применив эту формулу к случаю:

,

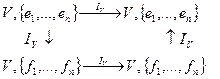Получим: 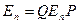, где Е_п – единичная матрица. Отсюда 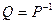. И, следовательно, если Р – матрица перехода от базиса 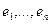к базису 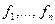, то матрицей перехода от базиса 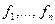к базису 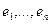.будет матрица Р^-1.

§ 5. Двойственное пространство и двойственное отображение.

Определение 14. Функционалом на линейном пространстве V называется отображение V в множество чисел.

Определение 15. Линейным функционалом на линейном пространстве V называется функционал F со свойством: для любых векторов V и для любых двух чисел α, β:

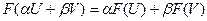
Введем для линейных функционалов, заданных на линейном пространстве V, структуру пространства следующим образом. Пусть f и g – линейные функционалы. Тогда для любого х из V и любого числа а:

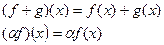
Предложение. f + g и 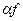- линейные функционалы.

Доказательство. .

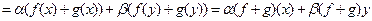Аналогично доказывается, что α f – линейные функционалы.

Теорема 5. Множество линейных функционалов, заданных на линейном пространстве V, образуют линейное пространство (относительно введенных операций).

Доказательство. Надо проверить 10 равенств, определяющих линейное пространство. Пусть х – любой вектор из V.

1. .

Следовательно, .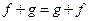

2.

Следовательно, .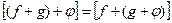

3. В качестве нулевого элемента возьмем нулевой функционал О*, т.е. функционал, равный 0 для всех векторов из V.

.

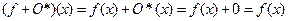Следовательно, .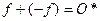

Аналогично проверяются оставшиеся равенства.

Определение 16. Введенное выше линейное пространство называется двойственным к линейному пространству V и обозначается V*.

Определение 17. Пусть в линейном пространстве V выбран базис 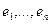. «Двойственным базисом» называется система функционалов 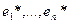из V* со свойством:

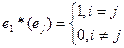
Заметим, что определение корректно, так как линейное отображение полностью определено своими значениями на векторах базиса, а сами эти значения могут заданы произвольно.

Теорема 6. «Двойственный базис» является базисом линейного пространства V*.

Доказательство. Пусть 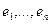- базис в линейном пространстве V, и 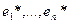- «двойственный базис». Пусть:

.

Тогда для любого i:

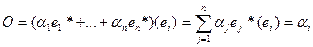. Следовательно, 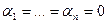и 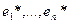линейно независимы. Пусть f - некоторый линейный функционал из V*, и пусть:

.

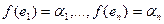Рассмотрим линейный функционал:

.

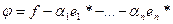Для любого х из V имеем: .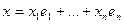

.

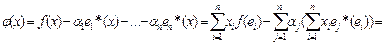
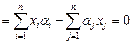Следовательно, 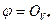. И мы получаем , что и доказывает теорему.

Определение 18. Пусть дано линейное отображение L: V₁→V₂ линейных пространств V₁ и V₂. Двойственным отображением называется отображение L*: V₁*→V₂* двойственных пространств, определенное формулой: L* 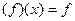(L (x)), где .

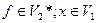Предложение. L* - линейное отображение.

Доказательство. Пусть α, β – произвольные числа, х – произвольный вектор из V₁, f и g – функционалы из V₂*.

.

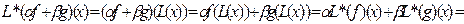
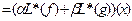Предложение доказано.

Предложение. Матрица двойственного отображения в двойственных базисах является транспонированной матрицей соответствующего линейного отображения.

Доказательство. Пусть:

L: V₁→V₂

L*: V₁*→V₂*

Зафиксируем в V₁ базис 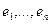, и в V₂ базис 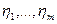. Пусть 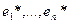и - двойственные базисы. L – матрица отображения L:

.

Тогда:

L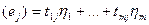

L* L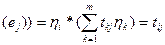

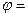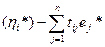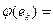Пусть L* .

L* .

Следовательно, и L* .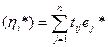

Тогда матрица L*, соответствующая отображению L*, имеет вид:

.

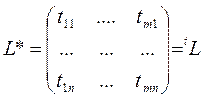Предложение доказано.

Теорема 7. rang L =rang L*.

Доказательство. Пусть:

L: V₁→V₂

L*: V₂*→V₁*

.

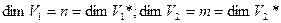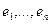- базис пространства V₁. Пусть rang L = 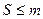. Это означает, что среди векторов L (е₁),… L (е_п) – S линейно независимых. Пронумеровав их, будем считать, что это вектора L (е₁),… L (е_S). Далее имеем:

(a)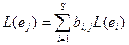

Дополним совокупность векторов до базиса пространства V₂: L (е₁),… L (е_S), 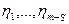. Рассмотрим двойственный базис:

L (е₁)*,… L (е_S)*, . Пусть тогда i=1…S

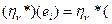L* L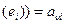

Рассмотрим:

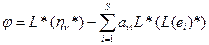
Тогда для любого j:

.

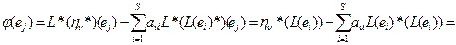
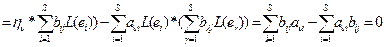Следовательно, - нулевое отображение, и:

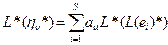
Итак, L* (η₁)*,… L* (η_т-S)* выражаются через L *(L (е₁)*),… L *(L (е_S)*).

Покажем, что последние линейно независимы. Пусть:

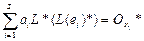
Тогда:

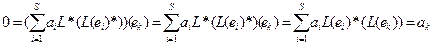
Следовательно, . Поэтому элементы L *(L (е₁)*),… L *(L (е_S)*) линейно независимы. Таким образом:

.

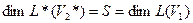Что и требовалось доказать.

Задачи к § 3, § 4, § 5.

1. Пусть в пространстве 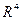задано отображение: .

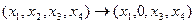А) доказать, что оно линейно.

Б) найти его матрицу в базисе:

.

2. Определить, какие из ниже перечисленных отображений являются линейными и найти ядра этих отображений.

А)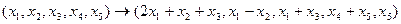

Б)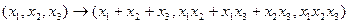

В)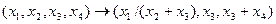

Г)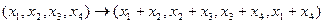

3. Даны 3 линейных отображения, переводящие заданные 3 вектора в заданные:

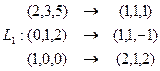и

Найти композицию L = L₂ ◦ L₁ этих отображений и матрицу этой композиции в базисе .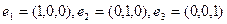

4. Линейное отображение L имеет в базисе матрицу:

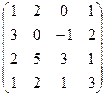
Найти матрицу этого преобразования в базисах:

А)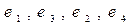

Б)

5. Линейное преобразование L в базисе 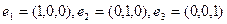имеет матрицу:

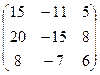
Найти его матрицу в базисе .

6. Существует ли линейное преобразование L, переводящее:

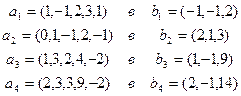
И если существует, то найти. Каким может быть его ранг.

7. Найти ранг линейного отображения L 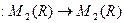, заданного формулой:

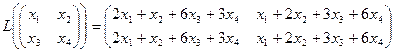
8. Найти ранг линейного отображения L , заданного формулой:

L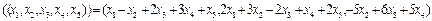

9. Существует ли линейное отображение со свойством: 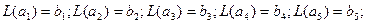где , , , , ; , ; , , .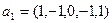

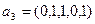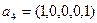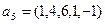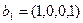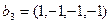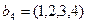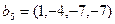10. Существует ли линейное отображение со свойством:

где 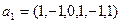, , 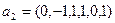, , 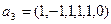, 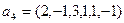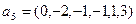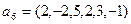; 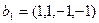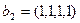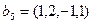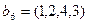, , , , ; ; и если существует, то найти его ранг.

Дата добавления: 2014-12-08