Планирование производства

Рассмотрим для начала простую задачу планирования производства. Предположим, что небольшая фабрика выпускает два вида красок: А и Б. Продукция поступает в оптовую продажу. Для производства используется два вида исходных продуктов: В и Г. Максимально возможные суточные запасы этих продуктов составляют 6т и 8т соответственно. Расходы про­дуктов на 1 т красок приведены в Таблице. I.

Таблица 1.

Исходный продукт	Расход на 1т краски	Максимальный запас
Краска А	КрасквБ
В Г

Анализ рынка показал, что суточный спрос на краску А не превышает спроса на краску Б более чем на 1т. Кроме того установлено, что спрос на А не превышает 2т в сутки. Прибыль от продажи красок А и Б равны 3 ОООр и 2 ОООр соответственно.

Необходимо найти количество выпускаемых красок, при котором при­быль максимальна.

Для решения задачи необходимо построить математическую модель, Дяя этого необходимо получать ответы на три вопроса:

1) для определения каких величия строится модель (переменные)?

2) что оптимизируется (функция цели)?

3) при каких условия определяется решение (ограничения)?

В нашем случае необходимо так спланировать объем производства красок, чтобы максимизировать прибыль. Поэтому переменными являются суточный объем производства красок ХА и ХБ.

Суммарная суточная прибыль от производства составляет:

П=3000*ХА+2000*ХБ

Перейдем к ограничениям. Объем производства не может быть отрицательным, следовательно

ХА,ХБ>=0.

Расход исходного продукта не может превосходить максимального запаса, следовательно

ХА+2*ХБ<=6,

2*ХА+ХБ<=8

Ограничение на спрос таковы, что должны выполняться неравенства

ХА-ХБ<=1,

ХБ<=2.

Математически задача формулируется следующим образом.

Необходимо максимизировать функцию

П=3000*XА+2000^*XБ

При ограничениях

ХА+2*ХБ<=6,

2*ХА+ХБ<=8,

ХА-ХБ<=1,

ХБ<=2,

ХА, ХБ>=0.

Решим поставленную задачу с помощью команд: Сервис, Поиск ре­шения. Если в меню Сервис отсутствует команда Поиск решения, то необ­ходимо выполнить последовательно: Сервис, Надстройка, Поиск решения.

Решение задачи начинаем с подготовки данных. Введем необходимые данные и ограничения следующим образом (Рис2)

Рис.2

Выберем команды: Сервис, поиск решения. Заполним окно диалога Поиск решения (Рис3).

Рис.3.

При этом параметры поиска в окне Параметры поиска решения

установлены следующим образом (Рис4).

Рис.4.

После команды Выполнить откроется окно диалога Результаты поиска решения, которое сообщает, что решение найдено (Рис5)

Рис.5.

Оптимальный план производства и соответствующая прибыль появятся в исходной таблице. Из нее следует, что оптимальным является производство 3,333т краски А и 1,333т краски Б. Этот объем производства обеспечивает максимальную прибыль 12666,7 (Рис7).

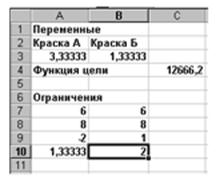Рис.7.

Для того чтобы вывести отчет о результатах решения, в окне Результаты поиска необходимо указать требуемый тип отчета: Результаты, Устойчивость, Пределы. Затем в рабочей книге выбрать появившийся корешок (Рис8)

Дата добавления: 2014-12-08