
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математична модель транспортної задачі
|
|
|
|
МЕТОДИ РОЗВ’ЯЗАННЯ ТРАНСПОРТНОЇ ЗАДАЧІ
ЗАВДАННЯ 3. У трьох пунктах виробництва А1, А2, А3 зосереджений однорідний вантаж у кількостях відповідно рівних а1, а2, а3 тонн. Даний вантаж споживається в чотирьох пунктах В1, В2, В3, В4, а потреби в ньому в цих пунктах складають b1, b2, b3, b4, тонн відповідно. Відома матриця тарифів по перевезенню 1 тони вантажу з i го пункту виробництва до j го пункту споживання:
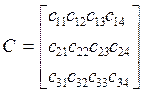 .
.
Скласти план перевезень:
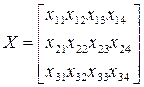 ,
,
при якому сумарні транспортні витрати будуть мінімальними.
Розв’язати поставлену транспортну задачу
3.1 методом потенціалів,
3.2 за допомогою інструмента «Поиск решения».
Розглянемо поставлену задачу для таких вихідних даних:
 30т,
30т, 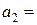 20т,
20т, 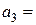 40т,
40т,
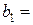 20т,
20т, 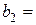 30т,
30т, 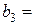 20т,
20т, 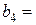 30т,
30т,
 .
.
Запишемо їх у вигляді таблиці.
Таблиця 3.1
| Пункти виробництва | Пункти споживання | Запаси | |||
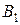
| 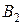
| 
| 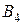
| ||
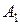
| |||||
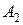
| |||||

| |||||
| Потреби |
До нижнього правого куту цієї таблиці занесемо значення сумарних потреб і сумарних витрат:
 т,
т, 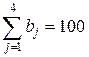 т.
т.
У даному випадку 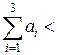
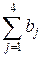 , тому модель транспортної задачі є відкритою. Відповідно до теореми, для існування в транспортної задачі припустимого плану необхідно і достатньо, щоб її модель була закритою, тобто, щоб
, тому модель транспортної задачі є відкритою. Відповідно до теореми, для існування в транспортної задачі припустимого плану необхідно і достатньо, щоб її модель була закритою, тобто, щоб 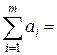
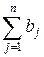 .
.
Збалансуємо дану задачу, уводячи фіктивний пункт виробництва  з запасом вантажу
з запасом вантажу 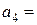
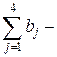
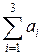 =100-90=10(т). При цьому вартість перевезень із цього пункту в кожний із пунктів споживання дорівнює 0 (див. табл. 3.2).
=100-90=10(т). При цьому вартість перевезень із цього пункту в кожний із пунктів споживання дорівнює 0 (див. табл. 3.2).
Таблиця 3.2
| Пункти виробництва | Пункти споживання | Запаси | |||
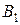
| 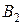
| 
| 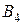
| ||
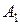
| |||||
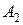
| |||||

| |||||

| |||||
| Потреби |
Складемо математичну модель даної задачі.
1. Змінні задачі:  – планований обсяг перевезення (у тоннах) з
– планований обсяг перевезення (у тоннах) з 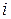 го пункту виробництва в
го пункту виробництва в 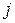 й пункт споживання (
й пункт споживання (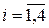 ,
,  ). Сукупність змінних
). Сукупність змінних 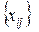 утворить матрицю
утворить матрицю
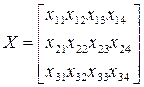 .
.
2. Цільова функція задачі виражає транспортні витрати, які необхідно мінімізувати:
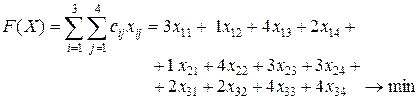 .
.
3. Обмеження задачі: на вивіз вантажу
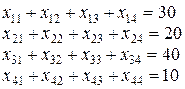 , (9)
, (9)
на задоволення потреб у вантажі
 , (10)
, (10)
невід’ємність змінних:
 (
(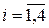 ,
,  ). (11)
). (11)
Сукупність змінних 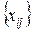 , що задовольняють обмеженням (9)-(11), утворюють припустимий опорний план. Матриця системи (9) ‑ (10) має ранг на 1 менший кількості рядків цієї системи, тобто на 1 менший від суми кількостей пунктів виробництва і пунктів споживання, у даному випадку це – 7. Це означає, що кількість базисних змінних повинна дорівнювати 7.
, що задовольняють обмеженням (9)-(11), утворюють припустимий опорний план. Матриця системи (9) ‑ (10) має ранг на 1 менший кількості рядків цієї системи, тобто на 1 менший від суми кількостей пунктів виробництва і пунктів споживання, у даному випадку це – 7. Це означає, що кількість базисних змінних повинна дорівнювати 7.
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 649; Нарушение авторских прав?; Мы поможем в написании вашей работы!