
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выбор контрольно-измерительных средств
|
|
|
|
ТЕХНОЛОГИЯ КОНТРОЛЯ ПАРАМЕТРОВ КАЧЕСТВА ДЕТАЛИ
Существуют различные подходы к выбору контрольно-измерительных средств. Далее приведены некоторые из них.
Выбор СИ по коэффициенту уточнения. Это самый простой способ, предусматривающий сравнение точности измерения и точности изготовления (функционирования) объекта контроля. Здесь предусматривается введение коэффициента уточнения 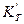 (коэффициента закона точности) при известном допуске Т и предельном значении
(коэффициента закона точности) при известном допуске Т и предельном значении  погрешности измерения
погрешности измерения
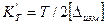 .
.
Величину, обратную 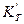 , называют относительной погрешностью метода измерения
, называют относительной погрешностью метода измерения
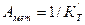 .
.
В соответствии с ГОСТ 8.051—81 значения пределов допускаемых погрешностей  для линейных размеров задаются в зависимости от допусков и квалитета (таблица 5.1) как
для линейных размеров задаются в зависимости от допусков и квалитета (таблица 5.1) как 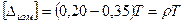 .
.
Таблица 5.1 - Зависимость 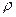 от диапазона допусков и квалитета
от диапазона допусков и квалитета
| Квалитет | 2—5 | 6—7 | 8—9 | 10—16 |
Средний коэффициент, 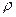
| 0,35 | 0,30 | 0,25 | 0,20 |
| Диапазон допусков, мкм | 0,8—2,7 | 6—63 | 14—155 | 40-4000 |
Диапазон [ 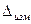 ], ±мкм ], ±мкм
| 0,25—10,00 | 2—19 | 3,5—39,0 | 8—800 |
Для линейных размеров указанное соотношение между  и Т от 20 до 35% соответствует
и Т от 20 до 35% соответствует 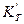 = 2,5 – 1,4.
= 2,5 – 1,4.
При выборе СИ по величине  необходимо иметь соответствующие справочные данные о погрешностях конкретных СИ.
необходимо иметь соответствующие справочные данные о погрешностях конкретных СИ.
Тогда, если измеряемый размер попадает в стандартизованный ГОСТ 8.051 —81 интервал О...500 мм, то используют среднее значение 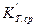 , а предел основной допускаемой погрешности СИ находят как
, а предел основной допускаемой погрешности СИ находят как

и из таблица 5.2 выбирают ближайшее СИ с такой погрешностью.
Таблица 5.2 - Предельные погрешности наиболее распространенных универсальных средств измерения
| Измерительные средства | Предельные погрешности измерения ( , мкм) для интервалов размеров, мм , мкм) для интервалов размеров, мм
| |||||||
| До 10 | 11…50 | 51…80 | 81…120 | 121…180 | 181…260 | 261…360 | 361…500 | |
| Оптиметры, измерительные машины (при измерении наружных размеров) | 0,7 | 1,0 | 1,3 | 1,6 | 1,8 | 2,5 | 3,5 | 4,5 |
| То же при (измерении внутренних размеров) | – | 0,9 | 1,1 | 1,3 | 1,4 | 1,6 | – | – |
| Микроскоп универсальный | 1,5 | 2,0 | 2,5 | 2,5 | 3,0 | 3,5 | – | – |
| То же | 5,0 | 5,0 | – | – | – | – | – | – |
| Миниметр с ценой деления: | ||||||||
| 1 мкм | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 4,5 | 6,0 | 8,0 |
| 2 мкм | 1,4 | 1,8 | 2,5 | 3,0 | 3,5 | 5,0 | 6,5 | 8,0 |
| 5 мкм | 2,2 | 2,5 | 3,0 | 3,5 | 4,0 | 5,0 | 6,5 | 8,5 |
| Рычажная скоба с ценой деления: | ||||||||
| 2 мкм | 3,0 | 3,5 | 4,0 | 4,5 | – | – | – | – |
| 10 мкм | 7,0 | 7,0 | 7,5 | 7,5 | 8,0 | – | – | – |
| Микрометр рычажный | – | – | – | – | – | – | ||
| Микрометр | ||||||||
| Индикатор | ||||||||
| Штангенциркуль с ценой деления: | ||||||||
| 0,02 мм | ||||||||
| 0,05 мм | ||||||||
| 0,10 мм |
Выбор СИ по принципу безошибочности контроля предполагает предварительную оценку вероятностей ошибок первого и второго рода.
Схема выбора СИ включает следующие этапы:
1. Оценивают (или обоснованно задают) законы распределения контролируемого параметра и погрешности измерения.
2. Задаются соответствующие вероятности ошибок первого и второго рола (или отдельно Р 1 и Р 2).
3. По таблице 5.3 находят соответствующее значение коэффициента уточнения 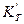 .
.
Таблица 5.3 - Вероятности Р 1 и Р 2 при контроле по размерным параметрам
Коэффициент, уточнения 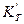
| Закон распределения контролируемых параметров | |||||||
| нормальный | Существенно-положительных величин | |||||||
| Закон распределения погрешности измерения | ||||||||
| нормальный | равномерный | нормальный | равномерный | |||||
| Р 1 | Р 2 | Р 1 | Р 2 | Р 1 | Р 2 | Р 1 | Р 2 | |
| 10,40 5,50 3,30 2,10 1,70 1,40 1,04 | 0,4 0,9 1,7 2,8 3,5 4,1 5,4 | 0,37 0,87 1,60 2,60 3,10 3,75 5,00 | 0,75 1,30 2,25 3,70 4,75 5,80 8,25 | 0,7 1,2 2,0 3,4 4,5 5,4 7,8 | 0,25 0,70 1,25 2,20 2,75 3,25 4,35 | 0,15 0,60 1,20 1,90 2,50 3,00 3,90 | 0,5 0,9 1,5 2,8 3,8 4,2 5,5 | 0,4 0,7 1,5 2,4 3,2 3,5 5,2 |
Примечание. Значения вероятностей Р 1 и Р 2 умножены на 100.
4. При известном допуске на параметр выбирают СИ по таблицам, аналогичным таблице 5.2.
Выбор СИ с учетом безошибочности контроля и его стоимости осуществляется как метод оптимизации по критериям точности (классу точности 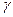 или абсолютной предельной погрешности
или абсолютной предельной погрешности  ) СИ, его стоимости Сси и достоверности измерения. Целевая функция G, определяющая максимум достоверности (минимум вероятности
) СИ, его стоимости Сси и достоверности измерения. Целевая функция G, определяющая максимум достоверности (минимум вероятности  неверного заключения) и минимум стоимости при оптимальном классе точности, имеет вид:
неверного заключения) и минимум стоимости при оптимальном классе точности, имеет вид:
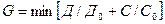 ,
,
где  ,
,  — относительные значения соответственно достоверности измерения и стоимости СИ;
— относительные значения соответственно достоверности измерения и стоимости СИ;  и С0 — соответственно максимальные значения достоверности измерения и стоимости СИ. Или:
и С0 — соответственно максимальные значения достоверности измерения и стоимости СИ. Или:
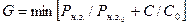 ,
,
где  ,
,  — относительная и максимальная вероятности неверного заключения.
— относительная и максимальная вероятности неверного заключения.
Соответственно для многопараметрического контроля по N параметрам (i = 1,2,..., N):
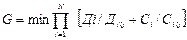

Следующий этап выполнения курсовой работы заключается в оценке возможного уровня дефектности, который может быть рассчитан по формуле:
q= П /А,
где П – потери от погрешности измерений; А – затраты на несоответствия; q – уровень дефектности партии ФИ.
Уровень дефектности (q) также можно представить через формулу:
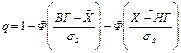 ,
,
где Ф(Z) – функция Лапласа; ВГ, НГ – верхняя и нижняя граница поля допуска соответственно;  - среднее значение поля рассеивания σS – среднее квадратическое отклонение рассеивание параметров [13].
- среднее значение поля рассеивания σS – среднее квадратическое отклонение рассеивание параметров [13].
Для одного из параметров детали разрабатываемого объекта необходимо определитть подходящее контрольно-измерительное средство. Для одной из деталей разрабатываемого объекта необходимо рассчитать уровень возможной дефектности
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 769; Нарушение авторских прав?; Мы поможем в написании вашей работы!