Основные уравнения

Уравнение неразрывности. Это уравнение имеет вид

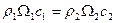. (4.3)

Применим это уравнение к одному межлопастному каналу, рассматривая лопасть длиной 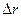(рис. 4.1). В пределах малой длины 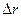можно полагать скорости постоянными. Площади входного и выходного сечений одинаковы, т.е.

.

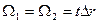В уравнении (4.3) векторы 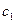и соответственно нормальны к плоскостям сечений 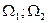. Поэтому, полагая 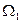и 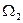нормальными к оси машины, следует считать 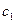и осевыми составляющими абсолютной скорости и обозначать индексом а. Из рис. 4.3 следует

; .

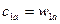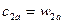Следовательно, уравнение неразрывности может быть записано после сокращения площади входного и выходного сечений 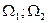так:

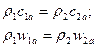(4.4)

Для несжимаемой жидкости 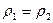, поэтому

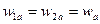; (4.5)

Уравнение энергии. В относительном движении через рабочее колесо осевой машины энергия потоку не сообщается; здесь происходит лишь преобразование кинетической энергии в потенциальную. Этот процесс сопровождается преобразованием энергии потока.

При изменении удельной кинетической энергии относительного движения от 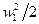до 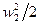происходит непрерывное изменение давления, плотности и уравнение энергии можно записать так:

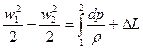, (4.6)

где 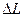- энергия, переходящая в теплоту.

Изменение потенциальной энергии, выражаемое интегралов в правой части равенства (4.6), может быть вычислено в случаях, когда известна зависимость между 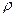и р, т.е. известен термодинамический процесс в межлопастном канале машины. В машинах низкого давления (вентиляторы) – это изотермический, а в осевых компрессорах – политропный процесс.

Энергия, сообщаемая потоку рабочей лопастной решёткой, может быть рассчитана по основному уравнению центробежной машины, в котором :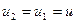

.

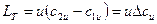Из планов скоростей (рис. 4.3) следует

;

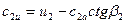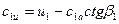
Подставляя значения 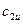и 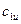в выражение для и используя выражение (4.5), получаем

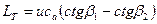. (4.7)

Уравнение энергии абсолютного движения через рабочую решётку осевой машины можно записать так:

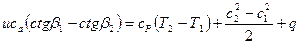(4.8)

Уравнения количества движения. Уравнения количества движения служат для расчёта сил взаимодействия между потоком и лопастями осевой машины. Пусть участок лопасти длиной 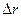действует на поток с силой Р (см. рис.4.1 и 4.4). Проекции этой силы: 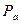- на ось машины и 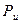- на ось решётки. Рассмотрим поток при относительном движении с шириной, равной шагу решётки.

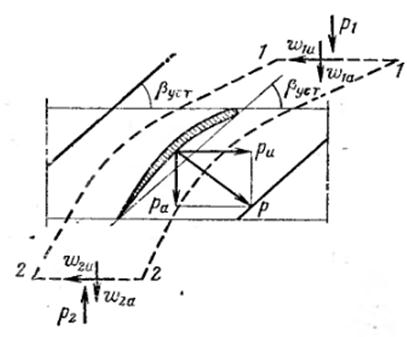
Рисунок 4.4 Применение теоремы импульсов к определению сил, действующих на лопасть

Через сечение 1-1 проходит с секунду масса 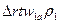, обладающая в направлении оси машины количеством движения 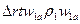, аналогично для сечения 2 – 2 .

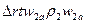Есл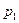и и 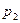- давления в сечениях 1 – 1 и 2 – 2 потока, то обусловливаемые ими силы – соответственно 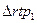и .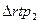

Импульс внешних сил, действующих на поток в направлении начальной1 скорости, равен изменению количества движения потока, поэтому

.

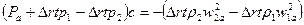Знак минус в правой части равенства указывает на то, что изменение количества движения рассматриваемого объёма жидкости вызывает силу, действующую на лопасть в направлении, обратном 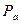. Следовательно,

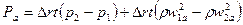. (4.9)

Для несжимаемой жидкости 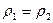и по уравнению (4.5) 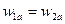, поэтому

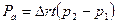(4.10)

Решётка профилей, перемещающая несжимаемую жидкость, не изменяет осевой скорости потока; осевая сила, приложенная к потоку, расходуется на повышение давления.

Применим уравнение количества движения для определения тангенциальной составляющей 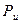. Для этого запишем уравнение количества движения в проекции на ось решётки.

Количество движения в сечениях 1 – 1 и 2 – 2

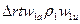и .

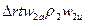Уравнение количества движения

.

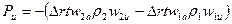Отсюда следует

.

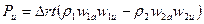Используя равенство (4.4), получаем

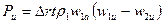. (4.11)

Результирующая получается геометрическим сложением сил 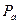и .

Уравнение циркуляции. Общее выражение для циркуляции

Легко применяется к профилю решётки. Рассматривая контур 1 -1 -2 -2 -1 (рис.4.4), представляем циркуляцию как сумму следующих интегралов:

.

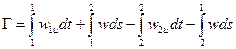Виду того что линии 1 – 2 и 2 – 1 геометрически одинаковы и скорости в соответствующих точках равны, второй и четвёртый интегралы сокращаются. Следовательно,

.

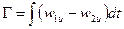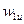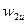Поскольку и - постоянные, средние по шагу величины,

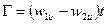(4.12)

Теорема Н.Е. Жуковского. Подъёмная сила лопасти с l = 1, движущейся в неограниченном пространстве, определяется теоремой Жуковского

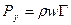(4.13)

где w – относительная скорость набегающего потока; Г – циркуляция по контуру, охватывающему лопасть.

Изолированная лопасть не изменяет параметров потока: относительная скорость перед лопастью и за нею одинакова. Решётка лопастей, как видно из рис. 4.3 изменяет значение и направление относительной скорости 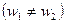. В этом заключается существенное различие в действии изолированной лопасти и решётки лопастей на поток.

Теорема Жуковского для лопасти решётки

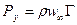(4.14)

Из рис. 4.3 ясно, что 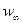представляет собой среднюю векторную скорость

.

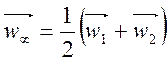В случае6 обтекания решётки газом плотность 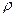в уравнении (4.14) можно полагать среднеарифметической плотностью входа и выхода.

Нетрудно убедиться, что направление силы 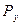нормально к вектору 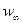(рис.4.5).

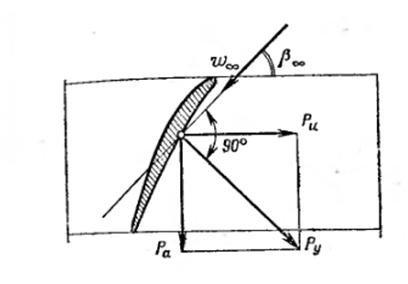
Рисунок 4.5 Силы, действующие со стороны лопасти на поток

Аэродинамические коэффициенты. Распространяя известный в аэродинамике способ расчёта сил, действующих на изолированную лопасть, на решётку профилей, можно записать

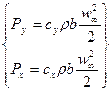(4.15)

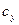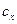где и - коэффициенты подъёмной силы и лобового сопротивления; и 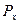- подъёмная и лобовая силы взаимодействия потока и профиля решётки.

Коэффициент 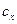может быть определён только опытным путём; приближённое значение 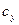можно найти теоретически, а точное – из опыта.

Сопоставляя уравнения (4.14) и первое из уравнений (4.15), получим

.

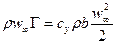Следовательно,

.

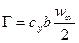Последнее уравнение совместно с уравнением (4.12) позволяет определить :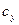

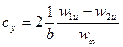
Из рис.4.3 имеем

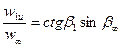и

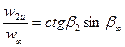
Поэтому

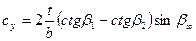(4.16)

Это равенство даёт возможность расчёта коэффициента 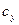по известным параметрам решётки профилей.

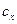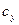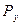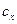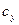Точные значения и получают путём продувки решёток лопастей различных форм при разных углах атаки; производя измерения скорости, плотности и сил и , производя расчёт и по уравнениям (4.15). Результаты продувок изображают графически, (рис.4.6).

Рисунок 4.6 Результаты испытания решётки при малых скоростях

Подобрав при проектировании диаграмму для решётки данного геометрического типа и задавая угол атаки, находят по диаграмме значения 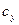и 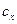и по формулам (4.15) вычисляют 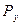и .

Дата добавления: 2014-12-08